
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Запишите формулу и сформулируйте, чему равен главный момент сил инерции механической системы
|
|
|
|
Запишите формулу и сформулируйте, чему равен главный вектор сил инерции механической системы.
Главный вектор: 
Главный вектор всех сил инерции механической системы равен производной по времени от количества движения системы, взятой с противоположным знаком.
Так как  , то для главного вектора сил инерции получаем формулу:
, то для главного вектора сил инерции получаем формулу:  , где: M - масса системы,
, где: M - масса системы, 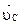 и
и  - скорость и ускорение центра масс.
- скорость и ускорение центра масс.
-Главный вектор сил инерции тела, совершающего любое движение, равен произведению его массы на ускорение центра масс и направлен в сторону, противоположную этому ускорению.
-Главный вектор сил инерции тела равен силе инерции его центра масс, если предположить, что в нем сосредоточена масса всего тела.
Главный момент: 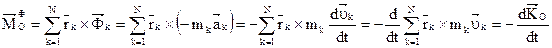
Главный момент сил инерции механической системы относительно неподвижного центра О равен производной по времени от кинетического момента (момента количества движения) механической системы, относительно того же центра, взятой с обратным знаком.
6. К чему приводятся силы инерции твердого тела в частных случаях его поступательного, вращательного и плоскопараллельного движения? Запишите соответствующие формулы.
Поступательное движение: Силы инерции точек тела приводятся к равнодействующей, геометрически равной главному вектору и приложенной в центре масс тела.

Вращательное движение: При приведении сил инерции точек тела при его вращательном движении вокруг неподвижной оси к произвольному центру, расположенному на этой оси, в общем случае силы инерции приводятся и к главному вектору, и к главному моменту.
В частном случае, когда тело имеет плоскость симметрии Сxy и вращающегося вокруг оси Сz, проходящей через центр масс С и перпендикулярной этой плоскости, главный вектор сил инерции равен нулю  , так как ускорение центра масс равно нулю. Следовательно, система сил инерции приводиться к одной паре, лежащей в плоскости симметрии Сxy, момент которой перпендикулярен этой плоскости и равен главному моменту сил инерции
, так как ускорение центра масс равно нулю. Следовательно, система сил инерции приводиться к одной паре, лежащей в плоскости симметрии Сxy, момент которой перпендикулярен этой плоскости и равен главному моменту сил инерции 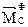 .
.
Для данного частного случая: 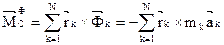 , где:
, где:  - радиус-вектор частицы тела относительно центра масс,
- радиус-вектор частицы тела относительно центра масс, 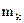 и
и 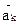 - масс и ускорение этой частицы.
- масс и ускорение этой частицы.


Главный момент сил инерции тела, совершающего вращательное движение, равен произведению его момента инерции относительно оси вращения, проходящей через центр масс и перпендикулярной плоскости симметрии тела и проекции углового ускорения на эту ось, и направлен противоположно этому ускорения.

Плоскопараллельное движение: Если твердое тело имеет плоскость материальной симметрии и движется параллельно этой плоскости, то силы инерции точек тела приводятся к силе, приложенной в центре масс тела C, и к паре сил, лежащей в плоскости симметрии. Сила равна главному вектору сил инерции, а величина момента пары равна главному моменту сил инерции.
 ;
;  - проекция момента пары лежащей в плоскости симметрии на ось, проходящую через центр масс тела С.
- проекция момента пары лежащей в плоскости симметрии на ось, проходящую через центр масс тела С.
7. Сформулируйте определение связи. Как математически выражаются связи, наложенные на систему?
Механическая система, точки которой могут занимать любое положение в пространстве и иметь любые скорости, называется свободной.
Если же на координаты и скорости точек наложены ограничения, не зависящие от приложенных активных сил и начальных условий, то система называется несвободной.
Ограничения движения точек механической системы, не зависящие от приложенных активных сил и начальных условий, называются связями.
Аналитическая запить связи:  ,
, 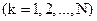 .
.
Ограничивая движение механической системы, связи действуют на точки системы посредством сил, которые называются силами реакции связей.
8. Какая связь называется стационарной, голономной, удерживающей? Приведите примеры.
1. Голономные
 ,
, 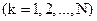 ,
, 
s - число уравнений связей.
N - количество материальный точек в механической системе.
Эти связи накладывают ограничения на координаты точек системы, а значит - на положение системы в пространстве. Такие связи называют геометрическими.
Голономные связи могут описываться и дифференциальными уравнениями, однако они должны быть обязательно интегрируемыми.
2. Неголономные
 ,
, 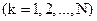 ,
, 
Эти связи накладывают ограничения на скорости точек системы, поэтому их называют кинематическими. Дифференциальные уравнения неголономной связи не интегрируются, то есть их нельзя привести к уравнениям голономной связи.
3. Стационарные
Это связи, выражающиеся уравнениями или неравенствами, не содержащими в явном виде время.
Например:  - это стационарная голономная связь.
- это стационарная голономная связь.
4. Нестационарные
Это связи, выражающиеся уравнениями или неравенствами, содержащими время в явном виде.
Например:  - это нестационарная голономная связь.
- это нестационарная голономная связь.
5. Удерживающие (двухсторонние)
Связь является таковой, если выражается равенством (=). Удерживающие связи сохраняют свое действие во все время движения точек системы.
6. Неудерживающие (односторонние)
Это связи, которые описываются неравенствами (<, >). Они могут в некоторые промежутки времени прекращать и возобновлять свое действие.
9. Дайте определение обобщенных координат механической системы. Каковы их обозначения?
Независимые между собой параметры, которые однозначно определяют положение механической системы в пространстве в любой момент времени, называются обобщенными координатами.
Обозначим обобщенные координаты механической системы через  ,
,  .
.
s - число уравнений связей.
N - количество материальный точек в механической системе.
10. Дайте определение действительного и возможного перемещения точки. Каковы их обозначения и различия?
На точку наложена голономная удерживающая связь. Точка перемещается по поверхности  (+). Этому уравнению удовлетворяют координаты точки в момент времени t.
(+). Этому уравнению удовлетворяют координаты точки в момент времени t.
Действительное перемещение:
Действительным перемещением точки за время dt называется такое элементарное перемещение, которое она фактически совершает в пространстве за время dt при данных связях. Действительное перемещение не зависит от действующих на точку сил, вида связи и от начальной скорости точки.
Через промежуток времени dt, под действием приложенных сил радиус-вектор точки 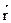 и ее координаты x, y, z изменятся. Точка получить действительное перемещение:
и ее координаты x, y, z изменятся. Точка получить действительное перемещение:  .
.
Уравнению связи (+) также должны удовлетворять новые координаты точки, то есть:
 .
.
Разложим эту функцию в ряд Тейлора до членов I-ого порядка: 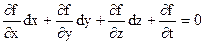 (#)
(#)
Это разложение представляет собой условие, которому должны удовлетворять проекции вектора 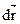 элементарного действительного перемещения точки.
элементарного действительного перемещения точки.
Известно, что координаты точек и, следовательно их радиус-вектора можно выразить через обобщенные координаты (§).
И тогда, действительное перемещение определяется совокупностью 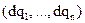 действительных приращений обобщенных координат, которые они получают в течение малого промежутка времени dt.
действительных приращений обобщенных координат, которые они получают в течение малого промежутка времени dt.
Элементарное действительное перемещение k-ой точки системы определяется как полный дифференциал функции  при переменном времени:
при переменном времени:

Возможное перемещение:
Возможным называется любое допускаемое связями перемещение материальной точки из положения, занимаемого ею в данный момент времени, в бесконечно близкое положение, которое она может занимать в тот же момент времени. Возможные перемещения не связаны ни с движением точки, ни с изменением наложенных на нее связей. Они представляют собой воображаемые перемещения, которые можно представить совокупностью бесконечно малых векторов, зависящих только от структуры связей, зафиксированных в рассматриваемый момент времени.
Вектор 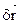 называют вариацией радиус-вектора точки, а проекции
называют вариацией радиус-вектора точки, а проекции 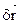 на оси декартовой системы координат - вариациями координат. Их обозначают
на оси декартовой системы координат - вариациями координат. Их обозначают 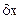 ,
,  ,
, 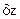 . Возможные перемещения должны удовлетворять дифференциальным соотношениям, вытекающим из уравнения связей, при условии, что время является фиксированным.
. Возможные перемещения должны удовлетворять дифференциальным соотношениям, вытекающим из уравнения связей, при условии, что время является фиксированным.
Пусть перемещение точки из положения, занимаемого ею в данный момент времени, в бесконечно близкое положение, допускаемое связями, происходит в результате изменения координат точки при фиксированном времени. Координаты точки с учетом вариации должны удовлетворять уравнению связи (+):  .
.
Разложим эту функцию в ряд Тейлора до членов I-ого порядка: 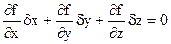 ($)
($)
При наличии связи  , вариации координат точки должны удовлетворять этому разложению. Так как t=const, то это разложение должно выполняться как для стационарных, так и для нестационарных связей. Для стационарной связи
, вариации координат точки должны удовлетворять этому разложению. Так как t=const, то это разложение должно выполняться как для стационарных, так и для нестационарных связей. Для стационарной связи 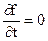 , и тогда разложение (#) совпадает с разложением ($).
, и тогда разложение (#) совпадает с разложением ($).
Следовательно, если связь стационарная, то элементарное действительное перемещение точки 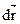 совпадает с одним из возможных
совпадает с одним из возможных 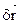 .
.
В случае нестационарной связи, проекции вектора 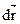 удовлетворяют условию (#), но не совпадают с разложением ($) для проекций вектора
удовлетворяют условию (#), но не совпадают с разложением ($) для проекций вектора 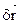 . В этом случае элементарное действительное перемещение точки не принадлежит к числу возможных.
. В этом случае элементарное действительное перемещение точки не принадлежит к числу возможных.
Известно, что координаты точек и, следовательно их радиус-вектора можно выразить через обобщенные координаты (§).
Таким образом, возможное перемещение системы определяется совокупностью  возможных перемещений обобщенных координат (время фиксировано).
возможных перемещений обобщенных координат (время фиксировано).
Возможное перемещение можно вычислить как полный дифференциал функции  при фиксированном времени:
при фиксированном времени:
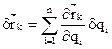
11. При каких связях действительное перемещение точки совпадает с одним из возможных?
Если связь стационарная, то элементарное действительное перемещение точки 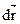 совпадает с одним из возможных
совпадает с одним из возможных 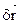 .
.
12. Дайте определение и запишите формулу возможной работы силы. Какие связи называются идеальными?
Возможной работой силы  называется работа силы на любом возможном перемещении точки ее приложения:
называется работа силы на любом возможном перемещении точки ее приложения:  .
.
Возможной работой сил 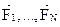 , приложенных к точкам механической системы в данный момент времени, называется работа, которую совершили бы эти силы на возможном перемещении системы:
, приложенных к точкам механической системы в данный момент времени, называется работа, которую совершили бы эти силы на возможном перемещении системы:
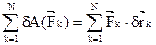 .
.
Связи называются идеальными, если возможная работа реакций связей на любом возможном перемещении системы из любого ее положения равна нулю.

13. Сформулируйте определение обобщенной силы. Каково аналитическое выражение обобщенной силы?
 (¨)
(¨)
Скалярную величину  называют обобщенной силой, соответствующей i-ой обобщенной координате.
называют обобщенной силой, соответствующей i-ой обобщенной координате.
Обобщенной силой, соответствующей некоторой обобщенной координате, называется величина, равная коэффициенту при вариации этой обобщенной координаты 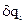 в выражении возможной работы всех активных сил, действующих на механическую систему (¨).
в выражении возможной работы всех активных сил, действующих на механическую систему (¨).
При изменении обобщенных координат, изменяются и обобщенные силы.
Обобщенная координата определяет размерность обобщенной силы.
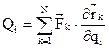
Аналитический способ вычисления обобщенной силы:
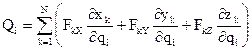
14. Если система находится в потенциальном силовом поле, то как выражаются обобщенные силы через потенциальную энергию?
Если силы приложенные к точкам системы потенциальные:
Потенциальная сила:  , поставим в
, поставим в 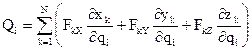
 - частная производная силовой функции
- частная производная силовой функции  по i-ой обобщенной координате.
по i-ой обобщенной координате.
Тогда: 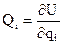 ,
, 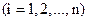
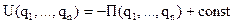 ,
,
то: 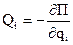 ,
, 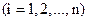
Если все действующие на систему силы потенциальны, то обобщенные силы равны частным производным от силовой функции по соответствующим обобщенным координатам.
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 879; Нарушение авторских прав?; Мы поможем в написании вашей работы!