Запишите формулы для кинетической и потенциальной энергии механической системы с одной степенью свободы при малых отклонениях от положения устойчивого равновесия

Пусть система, на которую наложены голономные, идеальные удерживающие и стационарные связи, состоит из N материальных точек и движется около положения устойчивого равновесия системы, где .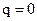

Кинетическая энергия:

По определению, кинетическая энергия системы: .

В силу стационарности наложенных на систему связей радиус-вектор 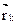каждой точки системы зависит только от обобщенной координаты q(t), то есть: 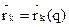. Тогда: , следовательно, кинетическая энергия равна: (²).

Величина A(q), как и 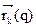, в общем случае является функцией обобщенной координаты q. Разложим функцию A(q) в окрестности положения равновесия (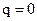) в ряд Маклорена. В результате получим:

(ã)

Индекс «0» означает, что соответствующие величины вычислены в положении равновесия, т.е. при .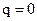

В силу малости колебаний в выражении (²) для кинетической энергии будем удерживать величины не выше II порядка малости, но так как в нем уже содержится величина II порядка - , то в разложении (ã) удержим только первый постоянный член, который обозначим «a». Итак, приближенное выражение кинетической энергии можно представить так: .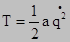

Положительная постоянна величина «а» называется коэффициентом инерции. Его размерность определяется размерностью обобщенной координаты. - квадрат обобщенной скорости.

Потенциальная энергия:

Потенциальная энергия является функцией обобщенной координаты. Разложим потенциальную энергию в степенной ряд в окрестности положения равновесия, помня, что в этом положении .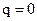

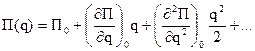(è)

Первый член в разложении (è) равен нулю, так как потенциальная энергия в положении равновесия равна нулю.

Второй член в этом разложении равен обобщенной силе, которая в положении равновесия также равна нулю.

В силу малости колебаний потенциальная энергия должна содержать члены не выше II порядка. Тогда:

Коэффициент при второй степени обобщенной координаты обозначим через «с» и назовем его обобщенным коэффициентом жесткости. Размерность «с» определяется размерностью обобщенной координаты.

С учетом введенного обозначения, окончательно имеем: .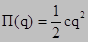

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

По теореме Лагранжа-Дирихле достаточным условием устойчивости положения равновесия является наличие в положении равновесия локального минимума П. Для этого необходимо равенство нулю первой производной (обобщенной силы) и положительность второй. Тогда условие c>0 является достаточным условием устойчивости колебательной системы с одной степенью свободы.

Дата добавления: 2015-03-31