Запишите дифференциальное уравнение малых движений системы с одной степенью свободы с учетом сил сопротивления

Рассмотрим механическую систему с одной степенью свободы, которая находиться в положении устойчивого равновесия. Пусть на точки системы, когда она выведена из положения равновесия, кроме потенциальных сил, начинают действовать диссипативные силы. Определим положение системы обобщенной координатой q, которую выберем так, что при равновесии .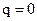

Для составления дифференциального уравнения воспользуемся уравнением Лагранжа II рода:

.

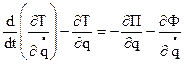Так как равновесие устойчиво, а возмущения малы, то обобщенная координата q и обобщенная скорость 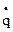во все время движения будут оставаться малыми величинами, а поэтому для определения кинетической и потенциальной энергии, а также диссипативной функции воспользуемся приближенными выражениями: , , .

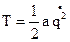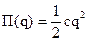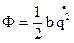Используя эти выражения находим: .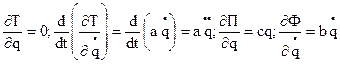

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Поставляя эти значения в уравнение Лагранжа, получим дифференциальное уравнение малых колебаний системы с одной степенью свободы с учетом сил сопротивления: 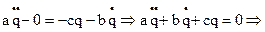, где: 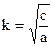= const, круговая или циклическая частота собственных колебаний системы без учета сил сопротивления, 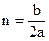= const, коэффициент затухания. Размерности у «n» и «k» одинаковые ().

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

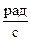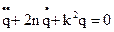- ОЛДУ II порядка с постоянными коэффициентами.

Его характеристическое уравнение: (; a = 1, b = 2n, c = )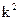

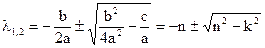
Характер движения системы будет существенно зависеть от соотношения между величинами «n» и «k».

1. n<k

Случай малого сопротивления. Характеристическое уравнение имеет два различных комплексных корня. Гармонические колебания.

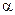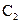Постоянные A, , и определяются из начальных условий: .

2. n=k

Случай критического сопротивления. Характеристическое уравнение имеет два кратных корня. Апериодическое движение.

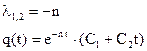
Постоянные и 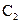определяются из начальных условий: .

3. n>k

Случай большого сопротивления. Характеристическое уравнение имеет два действительных корня. Апериодическое движение.

Постоянные и 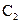определяются из начальных условий: .

Дата добавления: 2015-03-31