Запишите дифференциальное уравнение малых линейных колебаний системы с одной степенью свободы

Рассмотрим механическую систему с одной степенью свободы, которая находиться в положении устойчивого равновесия, под действием только потенциальных сил.

Определяем положение системы обобщенной координатой q, которую выберем так, что при равновесии .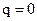

Для составления дифференциального уравнения воспользуемся уравнением Лагранжа II рода:

(ƒ)

Так как равновесие устойчиво, а возмущения малы, то обобщенная координата q и обобщенная скорость 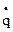во все время движения будут оставаться малыми величинами, а поэтому для определения кинетической и потенциальной энергии воспользуемся выражениями: , .

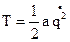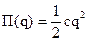Используя эти выражения находим: (©)

Подставляя значения (©) в уравнение (ƒ), получим дифференциальное уравнение малых колебаний системы с одной степенью свободы: 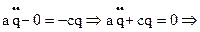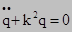, где: 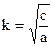= const, круговая или циклическая частота, которая имеет размерность угловой скорость (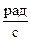) и не зависит от размерности обобщенной координаты.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

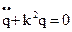- ОЛДУ II порядка с постоянными коэффициентами (Q).

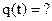
Характеристическое уравнение: (; a = 1, b = 0, c = )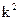

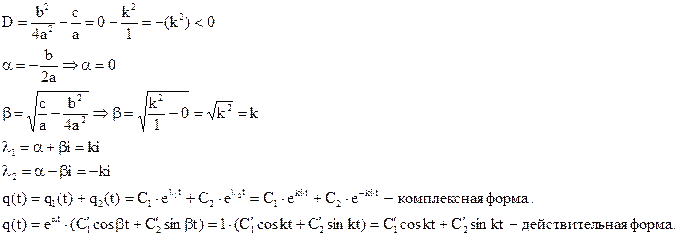
Произвольные постоянные 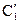и 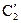определяем из начальных условий: .

Следовательно частным решением уравнения (Q), которое соответствует начальным условиям будет: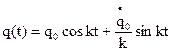

Приведем решение ОЛДУ II (Q) к амплитудной форме. Введем новые произвольные постоянные 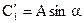и .

Тогда:

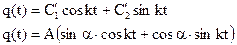
- закон движения системы (ù).

Величина А считается положительной и называется амплитудой колебаний. Одна определяет наибольшее отклонение обобщенной координаты q от положения равновесия, которое соответствует значению .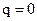

Как следует из решения (ù), обобщенная координата изменяется в пределах от +А до –А. Безразмерная постоянная 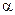называется начальной фазой колебаний. Она является значением фазы колебаний 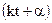при t = 0. Начальная фаза изменяется в пределах от 0 до .

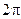Выразим A и 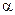через постоянные, 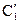и 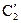определяемые из начальных условий: .

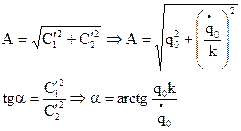
21. Запишите формулу периода малых линейных колебаний системы с одной степенью свободы. Что такое изохронизм колебаний?

Колебания системы, которые происходят под действием только потенциальных восстанавливающих сил, вызванные начальным отклонением точек системы или сообщением им начальной скорости называют свободными или собственными. Если при этом обобщенная координата q изменяется по закону синуса или косинуса, то колебания называются гармоническими. Как следует из (ù), свободные колебания в линейной консервативной системе с одной степенью свободы являются гармоническими. Следовательно, q(t) является периодической функцией.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Периодом свободных колебаний называется промежуток времени, в течение которого фаза колебаний изменяется на 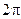, то есть наименьший промежуток времени, после которого движение повторяется.

, откуда: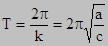

k - круговая или циклическая частота.

а - коэффициент инерции.

с - коэффициент жесткости.

Период колебаний изменяется в единицах времени. Величина называется частотой колебаний, которая измеряется числом колебаний в секунду или в Гц (герцах). Одно колебание в секунду соответствует одному герцу.

Величина периода, как и круговая частота, не зависят от начальных условий, а определяются только свойствами колеблющейся системы, то есть коэффициентом инерции и коэффициентом жесткости, поэтому их называют собственными характеристиками системы. Независимость периода и частоты колебаний от начальных условия называется изохронностью колебаний.

Гармонические колебания, возникнув в какой-то момент времени, продолжаются сколь угодно долго без изменений параметров, если нет других воздействий. Но обычно колебания всегда сопровождаются возникновением сил сопротивления, которые изменяют характер собственных колебаний.

Дата добавления: 2015-03-31