Межквартильный размах

Размах вариации

Размах вариации — это самая простая мера разброса набора данных. Размах вариации — промежуток между наибольшим и наименьшим значениями рас­пределения. На последующих примерах вы познакомитесь с порядком расчета размаха вариации.

Определение. Размах вариации — это простая мера вариации, вычисляемая путем вычитания наименьшего значения в наборе данных из наибольшего.

Пример. Найдем размах вариации на основании значений недельного дохода не­большого розничного предприятия за последние десять недель. (Данные приве­дены в тыс. ф. ст.)

12, 20, 15, 8, 5, 14, 22, 13, 10, 17.

Чтобы получить размах вариации, необходимо найти наибольшее и наи­меньшее значения в последовательности данных. Таковыми в данном приме­ре являются цифры 22 (максимальное значение) и 5 (минимальное значе­ние). Следовательно, размах вариации рассчитывается следующим образом:

Размах вариации = 22 — 5 = 17. Таким образом, для этих данных размах вариации составляет 17 000 ф. ст.

***Остальное в 9 и 10 вопросе

9.Что показывает и как находится межквартильный размах?

Размах, описанный в предыдущем разделе, имеет ряд недостатков. В це­лом, размах нельзя удовлетворительно применять при сравнении наборов дан­ных, так как он может быть легко искажен экстремальными отдельными зна­чениями. Например, в следующей таблице приведены данные по недельной заработной плате 100 работников предприятий А и Б соответственно:

Недельная заработная

плата (ф. ст.): 200- 300- 400- 500- 600- 700- 800- 900-

Количество

работников: предпр. А: 25 38 23 13 0 0 0 1

предпр. Б: 25 38 23 14 0 0 0 0

Размах для каждого набора данных составляет соответственно:

для предприятия А размах = 1000 — 200 = 800 ф. ст. для предприятия Б размах = 600 — 200 = 400 ф. ст.

Как видно, вариация согласно размаху для предприятия А в два раза боль­ше вариации для предприятия Б. Однако при исследовании исходных таблиц частот эту разницу можно отнести на счет единственного работника, получающего в интервале 900—1000, в сравнении с еще одним работником предприя­тия Б, получающим в интервале 500—600. Таким образом, одно экстремальное значение полностью исказило значение размаха. Поэтому на этот размах не стоит полагаться при проведении приемлемого сравнения наборов данных. Сле­довательно, требуется альтернативный способ определения величины вариации. Для этих целей приемлемой величиной считается значение межквартильного размаха. Межквартильный размах получают путем исключительного рассмотре­ния «размаха» для центральных 50% значений набора данных. На рис. 1.21 пред­ставлено распределение набора данных. Если мы опустим 25% наименьших зна­чений и 25% наибольших, тогда мы получим, как это показано на рисунке, размах, включающий центральные 50% значений, т. е. межквартильный размах. Два крайних значения из центральных 50% называются квартилями. Межквар­тильный размах (IQR) - расстояние между меньшей квартилью (Q,) и боль­шей квартилью (Q₃), как это показано на рисунке. Квартили можно подучить во многом аналогично тому, как мы определяли медиану ранее. Ведь медиа — это середина распределения и является [(n + 1)/2]-м порядковым значением.

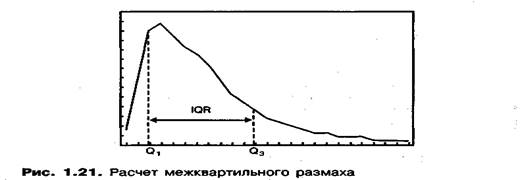
Аналогично, меньшая квартиль находится на расстоянии в 1/4 от начала распределения, а большая квартиль — на расстоянии в 3/4. Таким образом, эти квартили можно рассчитать следующим образом:

Меньшая квартиль, Q1 = 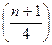-е порядковое значение;

Большая квартиль, Q3 = 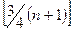-е порядковое значение. Имея эти значения, получаем межквартильный размах: .

Определение. Межквартильный размах — это разница между большей и меньшей квартилями. Данное значение показывает размах для центральных 50% данныx.

10. О чем говорят числовые характеристики по результатам выборки: выборочные среднее, дисперсия, среднее квадратическое отклонение, коэффициент вариации?

1.3 Средние величины: средняя, средневзвешенная, мода Мо, медиана Ме. Показатели вариации: дисперсия, среднее квадратическое отклонение, коэффициент вариации.

Среднее значение (иногда называемое показателем позиции или показателем центра) является наиболее важным специальным статистическим показателем, используемым для обобщения данных. Среднее значение дает представление о наиболее «типичном» или «центральном» значении в интервале изменения пере­менной. Часто опубликованные материалы, например отчеты предприятий, со­держат средние значения различных переменных. Например, средняя заработная плата, средний объем выпуска, средняя Продолжительность рабочей недели и сред­ний объем продаж — все эти термины часто встречаются в той или иной форме. При рассмотрении такого рода статистических показателей особое внимание сле­дует уделить точному выяснению методики расчета указанных средних. Имеется несколько таких методов, и каждый из них зачастую дает различные результаты. В данном разделе описаны три наиболее часто используемые в большинстве практи­ческих ситуаций «средние».

Определение. Средняя — это статистический показатель «середины» или «центра» исследуемых данных.

Дата добавления: 2015-04-23