Пример. Средняя набора значений может быть получена путем определения моды

Медиана

Мода

Средняя набора значений может быть получена путем определения моды. Моду можно коротко определить как значение, наиболее часто встречающе­еся в наборе данных. Это наиболее «типичное» значение среди данных, и часто его считают более репрезентативным, т.е. более достоверным, нежели среднюю арифметическую. На последующих примерах мы рассмотрим поря­док получения моды на основании данных, представленных в том или ином виде.

Определение. Мода — это средняя, получаемая путем установления наибо­лее часто встречающегося значения в наборе данных.

Пример. Нижеприведенные значения показывают количество работников, отсут­ствовавших на работе за период в 10 дней:

3, 5, 2, 1, 4, 3, 2, 0, 3, 6

Здесь видно, что наиболее часто встречается цифра 3. Отсюда мода равня­ется 3 работникам. Таким образом, среднее количество работников, отсутство­вавших на работе, можно определить как равное 3.

Пример. В таблице приведено количество отсутствовавших на работе за последние три недели (21 день):

Количество отсутствовавших: 0 1 2 3 4

Количество дней 2 8 6 3 2

Из таблицы частот следует, что чаще всего (8 дней) отсутствовало по одному работнику.

Таким образом, мода равняется 1 работнику. Как видно на примере такой простой таблицы частот, определение моды не представляет труда. Мы просто находим и соотносим ее со значением соответствующей пере­менной. Однако если таблица частот содержит интервалы группировки, то процесс определения становится более сложным.

Еще один способ определения среднего значения набора данных заключа­ется в получении медианы. В ряде случаев это наиболее приемлемый и очевидный вариант выявления центрального значения. В буквальном смысле, медиана — это срединное значение при условии, что данные выстроены в ранжирован­ном порядке. На последующих примерах вы познакомитесь со способом опреде­ления медианы.

Определение. Медиана — это среднее, полученное путем выявления «цент­рального» значения в перечне данных, расположенных в ранжированном порядке.

Рассмотрим таблицу частот, отображающую количество невыходов на ра­боту за период в три недели (21 день):

Количество отсутствовавших: 01234

Количество дней: 2 8 6 3 2

Согласно данной таблице, общее количество дней равно n = 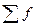= 21.

Отсюда медиана = [(n + 1)/2]-е или [(21 + 1)/2]-е = 11-е значение.

Теперь необходимо из этих данных выбрать 11-е значение. Есть 2 дня, в которые не отмечено невыходов; есть 8 дней, в которые отмечено по 1 невы­ходу. Следовательно, первые десять значений — это 0 или 1. Таким образом, 11-е значение — это 2. Итак, медиана равна 2-м работникам.

Дата добавления: 2015-04-23