КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема 2
Если вектор` b линейно выражается через векторы` a 1,` a 2 , ¼,` a k, то
L (` b,` a 1,` a 2 , ¼,` a k) = L (` a 1,` a 2 , ¼,` a k).
ДОКАЗАТЕЛЬСТВО.
Так как вектор` b линейно выражается через векторы` a 1,` a 2 , ¼,` a k, то` b = a 1` a 1 + a 2` a 2 + ¼ + a k ` a k.
Возьмем вектор`x Î L (` b,` a 1,` a 2 , ¼,` a k).
Тогда`x = l 0` b + l 1` a 1 + l 2` a 2 +¼+ l k ` a k =
= l 0 (a 1` a 1 + a 2` a 2 + ¼ + a k ` a k) + l 1` a 1 + l 2` a 2 + ¼ + l k ` a k =
= (l 0 a 1 + l 1)` a 1 + (l 0 a 2 + l 2)` a 2 +¼+ (l 0 a k + l k)` a k Î
Î L (` a 1,` a 2 , ¼,` a k) Þ L (` b,` a 1,` a 2 , ¼,` a k) Ì L (` a 1,` a 2 , ¼,` a k).
Возьмем вектор`x Î L (` a 1,` a 2 , ¼,` a k).
Тогда`x = l 1` a 1 + l 2` a 2 + ¼ + l k ` a k Þ
Þ`x = 0` b + l 1` a 1 + l 2` a 2 + ¼ + l k ` a k Þ`x Î L (` b,` a 1,` a 2 , ¼,` a k).
Следовательно, L (` a 1,` a 2 , ¼,` a k) Ì L (` b,` a 1,` a 2 , ¼,` a k).
Теорема доказана.
№ 3. ЛИНЕЙНО ЗАВИСИМЫЕ И ЛИНЕЙНО НЕЗАВИСИМЫЕ СИСТЕМЫ ВЕКТОРОВ. КРИТЕРИЙ ЛИНЕЙНОЙ ЗАВИСИМОСТИ.
Рассмотрим систему векторов` a 1,` a 2 , ¼,` a k. Нулевая линейная комбинация 0` a 1 + 0` a 2 + ¼ + 0` a k =`0, имеющая только нулевые коэффициенты, называется тривиальной линейной комбинацией векторов этой системы.
Существуют ли нетривиальные линейные комбинации векторов системы ` a 1,` a 2 , ¼,` a k, равные нулевому вектору`0? Ответ на этот вопрос зависит от свойств самой системы векторов` a 1,` a 2 , ¼,` a k.
Система векторов` a 1,` a 2 , ¼,` a k называется линейно зависимой, если существует нетривиальная нулевая линейная комбинация ее векторов, то есть существует линейная комбинация l 1` a 1 + l 2` a 2 + ¼ + l k ` a k =`0, в которой хотя бы один из коэффициентов отличен от нуля.
Система векторов` a 1,` a 2 , ¼,` a k называется линейно независимой, если не существует нетривиальной нулевой линейной комбинации ее векторов, то есть из равенства l 1` a 1 + l 2` a 2 + ¼ + l k ` a k =`0 следует, что
l 1 = l 2 = ¼ = l k = 0.
Например, линейно зависимой является система, состоящая из двух коллинеарных векторов в R2 или в R3, система из трех компланарных векторов в R3. Любые два неколлинеарных вектора в R2 или в R3, а также три некомпланарных вектора в R3 образуют линейно независимую систему.
Докажите это в качестве упражнения.
ОСНОВНЫЕ УТВЕРЖДЕНИЯ О ЛИНЕЙНО ЗАВИСИМЫХ СИСТЕМАХ.
УТВЕРЖДЕНИЕ 1.
Система, состоящая из одного вектора` a, линейно зависима тогда и только тогда, когда` a =`0.
ДОКАЗАТЕЛЬСТВО.
Пусть система, состоящая из одного вектора` a, линейно зависима, то есть существует линейная комбинация l` a =`0, в которой l ¹ 0. Тогда` a =`0.
Обратно. Если` a =`0, то 1` a =`0. Существование этой линейной комбинации доказывает линейную зависимость системы.
УТВЕРЖДЕНИЕ 2.
Для того, чтобы система, состоящая из двух ненулевых векторов` a и` b, была линейно зависимой, необходимо и достаточно, чтобы векторы` a и` b были пропорциональны.
ДОКАЗАТЕЛЬСТВО.
Пусть система, состоящая из векторов` a и` b, линейно зависима. Тогда существует линейная комбинация l 1` a + l 2` b =`0, в которой l 1 ¹ 0 или
l 2 ¹ 0. Тогда либо` a = 
` b, либо` b = 
` a, то есть векторы` a и` b пропорциональны.
Обратно. Если` a = l` b, то` a – l` b =`0, 1 ·` a – l` b =`0, 1 ¹ 0. Поскольку полученная нулевая линейная комбинация содержит ненулевой коэффициент, система, состоящая из векторов` a и` b, линейно зависима.
УТВЕРЖДЕНИЕ 3.
Если какая-либо часть системы векторов линейно зависима, то вся система линейно зависима.
ДОКАЗАТЕЛЬСТВО.
Пусть в системе векторов` a 1,` a 2 , ¼,` a m, ¼,` a k векторы
` a 1,` a 2 , ¼,` a m образуют линейно зависимую подсистему. Это означает, что существует линейная комбинация l 1` a 1 + l 2` a 2 + ¼ + l m ` a m =`0, в которой хотя бы один из коэффициентов отличен от нуля. Тогда линейная комбинация
l 1` a 1 + l 2` a 2 + l m ` a m + 0` a m + 1 + ¼+ 0` a k =`0 +`0 =`0 тоже содержит ненулевые коэффициенты. Отсюда следует, что система векторов
` a 1,` a 2 , ¼,` a m, ¼,` a k линейно зависима.
СЛЕДСТВИЯ.
1) Любая часть линейно независимой системы векторов линейно независима.
Это утверждение легко доказывается рассуждением от противного.
Предполагая, что некоторая часть линейно независимой системы является линейно зависимой, получаем противоречие утверждению 3.
2) Если в системе векторов имеется нулевой вектор или два пропорциональных (в том числе два равных) вектора, то эта система линейно зависима.
УТВЕРЖДЕНИЕ 4.
Если система векторов` a 1,` a 2 , ¼,` a k линейно независима, а система
` a 1,` a 2 , ¼,` a k,` b линейно зависима, то вектор` b линейно выражается через векторы` a 1,` a 2 , ¼,` a k.
ДОКАЗАТЕЛЬСТВО.
Так как система` a 1,` a 2 , ¼,` a k,` b линейно зависима, то существует линейная комбинация l 1` a 1 + l 2` a 2 +¼+ l k ` a k + l 0` b =`0, в которой хотя бы один из коэффициентов отличен от нуля. Докажем, что l 0 ¹ 0. Действительно, если l 0 = 0, то получаем нетривиальную линейную комбинацию
l 1` a 1 + l 2` a 2 + ¼ + l k ` a k =`0, существование которой противоречит линейной независимости системы векторов` a 1,` a 2 , ¼,` a k. Следовательно,
l 0 ¹ 0, и ` b = 
` a 1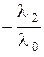 
` a 2 – ¼ 
` a k, что и требовалось доказать.
ТЕОРЕМА. Критерий линейной зависимости.
Для того чтобы система векторов` a 1,` a 2 , ¼,` a k была линейно зависимой необходимо и достаточно, чтобы хотя бы один из векторов этой системы можно было представить в виде линейной комбинации остальных.
ДОКАЗАТЕЛЬСТВО.
Пусть система векторов` a 1,` a 2 , ¼,` a k является линейно зависимой. Тогда существует линейная комбинация l 1` a 1 + l 2` a 2 + ¼ + l k ` a k =`0, в которой хотя бы один из коэффициентов отличен от нуля. Для определенности будем считать, что l 1 ¹ 0. Тогда ` a 1 = 
` a 2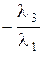 
` a 3 – ¼ 
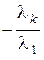` a k, то есть` a 1 Î L (` a 2 ,` a 3 , ¼,` a k).
Пусть теперь один из векторов (например,` a 1 ) линейно выражается через остальные, то есть` a 1 = l 2` a 2 + l 3` a 3 + ¼ + l k ` a k.
Тогда линейная комбинация` a 1 – l 2` a 2 – l 3` a 3 – ¼ – l k ` a k =`0 является нетривиальной, и система векторов` a 1,` a 2 , ¼,` a k линейно зависима. Теорема доказана.
№ 4. ТЕОРЕМА О ЗАМЕНЕ И ЕЁ СЛЕДСТВИЯ.
Пусть каждый вектор линейно независимой системы` b 1,` b 2 , …,` b m линейно выражается через векторы` a 1,` a 2 , ¼,` a k. Тогда
1) m £ k,
2) В системе` a 1,` a 2 , ¼,` a k можно какие – либо m векторов заменить на векторы` b 1,` b 2 , …,` b m так, что линейная оболочка полученной системы векторов будет совпадать с линейной оболочкой системы` a 1,` a 2 , ¼,` a k.
3) Если система` a 1,` a 2 , ¼,` a k линейно независима, то система векторов,
полученная в результате указанной замены, тоже является линейно независимой.
Без доказательства.
СЛЕДСТВИЕ 1.
Если системы векторов` a 1,` a 2 , ¼,` a k и` b 1,` b 2 , …,` b m линейно независимы, причем` a 1,` a 2, ¼,` a k Î L (` b 1,` b 2, …,` b m) и` b 1,` b 2, …,` b m Î
Î L (` a 1,` a 2 , ¼,` a k), то m = k.
ДОКАЗАТЕЛЬСТВО.
Применим теорему о замене два раза.
Поскольку ` a 1,` a 2 , ¼,` a k Î L (` b 1,` b 2 , …,` b m), то k £ m, а так как ` b 1,` b 2 , …,` b m Î L (` a 1,` a 2 , ¼,` a k), то m £ k. Следовательно, m = k.
СЛЕДСТВИЕ 2.
Если` b 1,` b 2 , …,` b m Î L (` a 1,` a 2 , ¼,` a k) и m > k, то система векторов` b 1,` b 2 , …,` b m линейно зависима.
ДОКАЗАТЕЛЬСТВО.
Предположим, что система` b 1,` b 2 , …,` b m линейно независима. Тогда по теореме m £ k, что противоречит условию. Следовательно, система
` b 1,` b 2 , …,` b m линейно зависима.
СЛЕДСТВИЕ 3.
В пространстве R n любая система, содержащая более n векторов, линейно зависима.
ДОКАЗАТЕЛЬСТВО.
Рассмотрим систему векторов` b 1,` b 2 , …,` b m пространства R n (m > n). Так как R n совпадает с линейной оболочкой системы векторов` e 1,` e 2,…,` e n, то` b 1,` b 2 , …,` b m Î L (` e 1,` e 2 , …,` e n), и, следовательно, по следствию 2 система` b 1,` b 2 , …,` b m линейно зависима.
№ 6. ОПРЕДЕЛЕНИЕ БАЗИСА ПОДПРОСТРАНСТВА ПРОСТРАНСТВА R n . СВОЙСТВА БАЗИСОВ. БАЗИСЫ ПРОСТРАНСТВА R n . КООРДИНАТЫ ВЕКТОРА В ДАННОМ БАЗИСЕ. ИХ ЕДИНСТВЕННОСТЬ.
1.БАЗИС И РАЗМЕРНОСТЬ ПОДПРОСТРАНСТВА ПРОСТРАНСТВА R n.
Пусть L — подпространство пространства R n.
Базисом подпространства L называется система векторов этого подпространства, которая удовлетворяет двум условиям:
– эта система линейно независима;
– эта система порождает подпространство L, то есть любой вектор подпространства L может быть представлен в виде линейной комбинации векторов этой системы.
СВОЙСТВА БАЗИСА.
1) Базис является наименьшей из систем, порождающих подпространство L. Это означает, что если из базиса убрать хотя бы один вектор, то оставшиеся векторы уже не будут порождать L, так как удаленный из базиса вектор принадлежит L, но его невозможно линейно выразить через оставшиеся векторы базиса в силу линейной независимости базиса.
2) Базис является максимальной линейно независимой системой векторов подпространства L. Если к базису добавить произвольный вектор подпространства L, то эта расширенная система векторов уже не будет линейно независимой, так как добавленный вектор линейно выражается через базисные векторы.
3) Любую линейно независимую систему векторов из L можно достроить до базиса подпространства L.
Действительно, если` a 1,` a 2 , ¼,` a k — некоторый базис L, а` b 1,` b 2 ,…,` b m — линейно независимая система векторов этого подпространства, то
` b 1,` b 2 , …,` b m Î L (` a 1,` a 2 , ¼,` a k) = L и по теореме о замене в базисе
` a 1,` a 2 , ¼,` a k можно какие – то m векторов заменить на векторы
` b 1,` b 2 , …,` b m так, что полученная система векторов будет порождать то же подпространство L и будет линейно независимой в силу линейной независимости системы` a 1,` a 2 , ¼,` a k.
4) Все базисы подпространства L содержат одинаковое количество векторов.
Действительно, если` a 1,` a 2, ¼,` a k и` b 1,` b 2, …,` b m — два базиса подпространства L, то обе системы линейно независимы,` a 1,` a 2, ¼,` a k Î
Î L (` b 1,` b 2, …,` b m),` b 1,` b 2, …,` b m Î L (` a 1,` a 2, ¼,` a k). По следствию 1 из теоремы о замене m = k.
Последнее свойство дает возможность определить понятие размерности подпространства.
Размерностью dim L подпространства L называется количество векторов в каком – либо базисе этого подпространства. Так, если` a 1,` a 2, ¼,` a k — некоторый базис подпространства L, то dim L = k.
СВОЙСТВА РАЗМЕРНОСТИ.
– Если L 1 и L 2 — два подпространства пространства R n, причем L 1 Ì L 2, то dim L 1 £ dim L 2.
В самом деле, если` a 1,` a 2, ¼,` a k и` b 1,` b 2, …,` b m — базисы подпространств L 1 и L 2 соответственно, то dim L 1 = k, dim L 2 = m,` a 1,` a 2, ¼,` a k Î Î L 1 Ì L 2 = L (` b 1,` b 2 , …,` b m). По теореме о замене получаем, что k £ m, то есть dim L 1 £ dim L 2.
– Если` b 1,` b 2 , …,` b m Î L, dim L = k, m > k, то система векторов
` b 1,` b 2 , …,` b m линейно зависима.
Действительно, если` a 1,` a 2 , ¼,` a k — базис L, то` b 1,` b 2 , …,` b m Î L =
=L (` a 1,` a 2 , ¼,` a k), и система` b 1,` b 2 , …,` b m линейно зависима по следствию 2 из теоремы о замене.
2.БАЗИСЫ ПРОСТРАНСТВА R n.
Поскольку пространство R n является подпространством самого себя, то к нему применимо определение базиса подпространства.
Базисом пространства R n называется система векторов этого пространства, которая удовлетворяет двум условиям:
– эта система линейно независима;
– эта система порождает пространство R n, то есть любой вектор пространства R n может быть представлен в виде линейной комбинации векторов этой системы.
Все свойства базисов подпространства справедливы и для базисов пространства R n.
Рассмотрим в R n векторы` e 1 = (1, 0, …,0),` e 2 = (0, 1, …,0), …,
` e n = (0, 0, …, 1). Докажем, что эта система векторов образует базис пространства R n. Было доказано, что L (` e 1,` e 2 , …,` e n) = R n. Следовательно, система векторов` e 1,` e 2 , …,` e n порождает пространство R n. Проверим ее линейную независимость. Составим нулевую линейную комбинацию
l 1`e 1 + l 2`e 2 + ¼ + l n `e n =`0. Докажем, что все ее коэффициенты равны нулю. Перепишем линейную комбинацию в виде
l 1 (1, 0, …, 0) + l 2 (0, 1, …, 0) + … + l n (0, 0, …, 1) = (0, 0, …, 0). Выполнив умножение векторов на числа и сложение векторов, получим равенство
(l 1, l 2 , …, l n ) = (0, 0, …, 0), из которого следует, что l 1 = l 2 = ¼ = l n = 0, а система векторов` e 1,` e 2, …,` e n линейно независима.
Система векторов` e 1,` e 2, …,` e n называется стандартным базисом пространства R n.
Наличие стандартного базиса доказывает, что все базисы пространства R n имеют ровно n векторов, и dim R n = n.
Применяя свойства размерности, получим, что размерность произвольного подпространства L пространства R n не превышает n, а любая система векторов из R n, имеющая более n векторов, линейно зависима.
ТЕОРЕМА.
В пространстве R n любая линейно независимая система, имеющая n векторов, является базисом этого пространства.
ДОКАЗАТЕЛЬСТВО.
Пусть` a 1,` a 2 , ¼,` a n — линейно независимая система векторов пространства R n, а` e 1,` e 2, …,` e n — стандартный базис этого пространства. Тогда` a 1,` a 2 , ¼,` a n Î L (` e 1, ` e 2, …,` e n ) = R n. Согласно теореме о замене можно все векторы` e 1,` e 2, …,` e n заменить на векторы` a 1,` a 2 , ¼,` a n, так что L (` a 1,` a 2 , ¼,` a n ) = L (` e 1,` e 2, …,` e n ) = R n. Следовательно, для системы векторов` a 1,` a 2 , ¼,` a n оба условия из определения базиса выполняются, и она является базисом пространства R n.
3. КООРДИНАТЫ ВЕКТОРА В ДАННОМ БАЗИСЕ. ИХ ЕДИНСТВЕННОСТЬ.
Рассматривая понятия базисов подпространства, пространства R n, системы векторов, заметим, что во всех случаях базис обладает свойством линейной независимости и способностью представлять в виде линейных комбинаций своих векторов векторы подпространства, пространства R n, системы векторов соответственно. Докажем единственность такого представления.
ТЕОРЕМА.
Любой вектор`x (подпространства, пространства R n, системы векторов) представляется в виде линейной комбинации базисных векторов единственным образом.
ДОКАЗАТЕЛЬСТВО.
Пусть` a 1,` a 2 , ¼,` a k — данный базис. Предположим, что существуют два различных представления вектора`x в виде линейной комбинации базисных векторов:
`x = l 1` a 1 + l 2` a 2 + ¼ + l k ` a k и`x = m 1` a 1 + m 2` a 2 + ¼ + m k ` a k .
Поскольку`x –`x =`0, то
l 1` a 1 + l 2` a 2 + ¼ + l k ` a k – (m 1` a 1 + m 2` a 2 + ¼ + m k ` a k) =`0,
(l 1 – m 1) ` a 1 + (l 2 – m 2 )` a 2 + … + (l k – m k )` a k =`0, откуда, в силу линейной независимости базисных векторов следует, что
l 1 – m 1 = 0, l 2 – m 2 = 0, …, l k – m k = 0 и, следовательно,
l 1 = m 1, l 2 = m 2, …, l k = m k. Таким образом, рассмотренные разложения вектора`x по базису совпадают. Теорема доказана.
Справедливость доказанного утверждения позволяет дать следующее определение.
Координатами вектора `x в данном базисе называются коэффициенты в разложении вектора`x по данному базису.
Заметим, что координаты вектора`x в данном базисе определяются однознач- но, но в разных базисах один и тот же вектор`x имеет разные координаты.
№ 7. РАЗМЕРНОСТЬ ПОДПРОСТРАНСТВА. СВОЙСТВА. РАЗМЕРНОСТЬ ПРОСТРАНСТВА Rn
Размерностью dim L подпространства L называется количество векторов в каком – либо базисе этого подпространства. Так, если` a 1,` a 2, ¼,` a k — некоторый базис подпространства L, то dim L = k.
СВОЙСТВА РАЗМЕРНОСТИ.
– Если L 1 и L 2 — два подпространства пространства R n, причем L 1 Ì L 2, то dim L 1 £ dim L 2.
В самом деле, если` a 1,` a 2, ¼,` a k и` b 1,` b 2, …,` b m — базисы подпространств L 1 и L 2 соответственно, то dim L 1 = k, dim L 2 = m,` a 1,` a 2, ¼,` a k Î Î L 1 Ì L 2 = L (` b 1,` b 2 , …,` b m). По теореме о замене получаем, что k £ m, то есть dim L 1 £ dim L 2.
– Если` b 1,` b 2 , …,` b m Î L, dim L = k, m > k, то система векторов
` b 1,` b 2 , …,` b m линейно зависима.
Действительно, если` a 1,` a 2 , ¼,` a k — базис L, то` b 1,` b 2 , …,` b m Î L =
=L (` a 1,` a 2 , ¼,` a k), и система` b 1,` b 2 , …,` b m линейно зависима по следствию 2 из теоремы о замене.
№ 8. Базис и ранг системы векторов. Их свойства.
Базисом системы векторов называется ее подсистема (часть системы), которая удовлетворяет двум условиям:
эта подсистема линейно независима;
любой вектор исходной системы может быть представлен в виде линейной комбинации векторов этой подсистемы.
СВОЙСТВА БАЗИСОВ.
Базис является максимальной линейно независимой подсистемой векторов данной системы.
Любая система векторов, имеющая хотя бы один ненулевой вектор, обладает базисом.
Все базисы данной системы векторов имеют одинаковое количество векторов.
Эти свойства предлагается доказать в качестве упражнения.
Рангом системы векторов называется число r, равное количеству векторов в каком – либо базисе этой системы. Иными словами, рангом системы векторов называется максимальное количество линейно независимых векторов данной системы.
СВОЙСТВА РАНГОВ.
Если` a 1,` a 2 , ¼,` a k Î L (` b 1,` b 2 , …,` b m), то ранг системы
` a 1,` a 2 , ¼,` a k не превосходит ранга системы` b 1,` b 2 , …,` b m.
Действительно, если r (a) и r (b) — ранги систем` a 1,` a 2 ,¼,` a k и
` b 1,` b 2 ,…,` b m соответственно, то, обозначая через` a 1,` a 2 , ¼,` a r ( a ) и
` b 1,` b 2 ,…,` b r ( b ) базисы соответствующих систем, получим
` a 1,` a 2 ,¼,` a r ( a ) Î L (` b 1,` b 2 , …,` b m ) = L (` b 1,` b 2 , …,` b r ( b )), откуда по теореме о замене следует, что r (a) £ r (b).
СЛЕДСТВИЕ.
Ранг подсистемы не превышает ранга системы векторов.
Если` a 1,` a 2 , ¼,` a k Î L, dim L = m, r — ранг системы` a 1,` a 2 , ¼,` a k, то r £ m. Доказательство аналогично доказательству свойства 1).
Если количество векторов в системе векторов больше ранга этой системы, то данная система векторов является линейно зависимой.
ДОКАЗАТЕЛЬСТВО.
Пусть` a 1,` a 2 , ¼,` a r — подсистема, являющаяся базисом данной системы векторов. Поскольку количество векторов в системе векторов больше ранга этой системы, то в данной системе существует хотя бы один вектор, не вошедший в указанный базис. Этот вектор линейно выражается через базис, и, следовательно, исходная система линейно зависима в силу критерия линейной зависимости.
№ 9. ОЖИ: ЖАРДАНОВЫ ТАБЛИЦЫ И ИХ ТРАКТОВКА. ОПРЕДЕЛЕНИЕ ОДНОГО ШАГА ОЖИ. АЛГОРИТМ ОТЫСКАНИЯ БАЗИСА СИСТЕМЫ ВЕКТОРОВ.
|
|
Дата добавления: 2015-04-24; Просмотров: 677; Нарушение авторских прав?; Мы поможем в написании вашей работы!