Определение одного шага ОЖИ

ЖОРДАНОВЫ ТАБЛИЦЫ И ИХ ТРАКТОВКА.

Пусть имеется две системы переменных x ₁, x ₂, …, x _n и y ₁, y ₂, …, y _m, которые связаны между собой соотношениями:

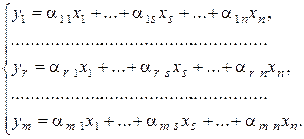
(1)

Эти соотношения можно записать в виде таблицы

	x 1	…	x s	…	x n
y 1 =	a 11	…	a 1 s	…	a 1 n
…	…	…	…	…	…		(2)
y r =	a r 1	…	a r s	…	a r n
…	…	…	…	…	…
y m =	a m 1	…	a m s	…	a m n

Например, соотношения 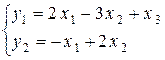можно записать в виде таблицы

	x 1	x 2	x 3	(3)
y 1 =		–3
y 2 =	–1

Наоборот, из таблицы

	a 1	a 2	a 3
b 1 =		–1
b 2 =			–2

можно выписать соотношения

Пусть в таблице (2) элемент a _{r s} отличен от нуля. Назовем его разрешающим элементом, а строку и столбец, содержащие его, назовем разрешающей строкой и разрешающим столбцом. При выполнении одного шага ОЖИ для таблицы (2) с разрешающим элементом a _{r s} переменные y _r и x _s меняются местами, а элементы таблицы пересчитываются по следующим правилам:

на место разрешающего элемента ставится 1;

оставшиеся элементы разрешающего столбца переписываются без изменения;

оставшиеся элементы разрешающей строки переписываются с противоположным знаком;

остальные элементы таблицы пересчитываются по правилу прямоугольника: на место элемента a _{i j} ставится число, равное значению выражения

a _{i j} a _{r s} – a _{r j} a _{i s}:

a i s	…	a i j
…	…	…
a r s	…	a r j

a i j	…	a i s
…	…	…
a r j	…	a r s

все элементы полученной таблицы делятся на разрешающий элемент a _{r s}.

Пересчет таблицы (2) по правилам 1) — 5) называется одним шагом ОЖИ с разрешающим элементом a _{r s}.

В качестве примера выполним один шаг ОЖИ для таблицы (3), взяв в качестве разрешающего элемента a _{r s} элемент a _{2 2} = 2.

	x 1	x 2	x 3
y 1 =		–3
y 2 =	–1

	x 1	y 2	x 3	: 2
y 1 =		–3
x 2 =

Þ

	x 1	y 2	x 3
y 1 =	1 / 2	–3 / 2
x 2 =	1 / 2	1 / 2

Полученная таблица соответствует системе уравнений

(4)

Систему уравнений (4) можно было получить без применения ОЖИ из системы уравнений 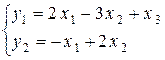, соответствующей таблице (3), непосредственным выражением переменной x ₂ из второго уравнения и подстановкой его в первое уравнение:

, Þ

Один шаг ОЖИ с разрешающим элементом a _{r s} равносилен выражению переменной x _s из уравнения

системы (1) и подстановке полученного выражения в остальные уравнения этой системы.

ЗАМЕЧАНИЕ. Если в системе (1) и, соответственно, в таблице (2) переменные x ₁, x ₂, …, x _n и y ₁, y ₂,…, y _m являются векторами, то справедливо соотношение y ₁, y ₂, …, y _m Î L (x ₁, x ₂, …, x _n) и один шаг ОЖИ соответствует одному шагу замены векторов, описанной в теореме о замене.

Дата добавления: 2015-04-24