
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Гипербола
|
|
|
|
№ 173. Асимптотами гиперболы являются прямые 4у ± 3х = 0. Записать ее каноническое уравнение.
Ответ: 
 .
.
№ 174. Найти вершины, фокусы, эксцентриситет и асимптоты гиперболы 
Ответ: (-3n; 0); (3n; 0);  ,
, 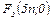 ;
; 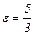 ;
; 
№ 175. Доказать, что отрезок касательной к гиперболе между ее асимптотами точкой касания делится пополам.
№ 176. Найти длины осей, координаты фокусов и эксцентриситет гиперболы, заданной уравнением:
а) 144х2 – 25у2 = 3600; б) 9у2 – 16х2 = 144.
Ответ: а) a = 5; b) = 12; (-13; 0); (13; 0);  . б) a = 3; b = 4; (0; -5); (0; 5);
. б) a = 3; b = 4; (0; -5); (0; 5); 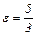 .
.
№ 177. На гиперболе 16х2 – 9у2 = 144n2 взята точка с абсциссой 3. Вычислите фокальные радиусы этой точки.
Ответ: 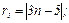
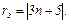
№ 178. Найти эксцентриситет гиперболы, если расстояние между ее директрисами в четыре раза меньше расстояния между фокусами.
Ответ: 
№ 179. Дан эллипс 5х2 + 9у2 = 45. Составить уравнение гиперболы, вершины которой находятся в фокусах, а фокусы в вершинах данного эллипса.
Ответ: 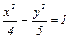
№ 180. Составить уравнение гиперболы, если ее асимптотами являются прямые 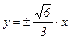 и она проходит через точку А (6,
и она проходит через точку А (6,  ).
).
Ответ: 
№ 181. Найти расстояние от начала координат до прямой, проходящей через центр гиперболы 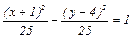 и вершину параболы у = – х2 + 2х – 1/3. Составить уравнение окружности, касающейся гиперболы в ее вершинах.
и вершину параболы у = – х2 + 2х – 1/3. Составить уравнение окружности, касающейся гиперболы в ее вершинах.
Ответ: 
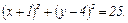
№ 182. Составить уравнение линии, для каждой точки которой отношение расстояний до точки
F (6,1) и до прямой х = 4,2 равно 1,25.
Ответ: 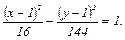
№ 183. Составить уравнение конического сечения с фокусом F (5,0), директрисой 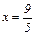 и эксцентриситетом
и эксцентриситетом 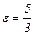 . Построить его.
. Построить его.
Ответ: 
№ 184. Найти все характеристики гиперболы 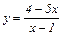 . Построить ее.
. Построить ее.
Ответ: 
 с = 2;
с = 2; 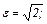
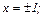

№ 185. Составить каноническое уравнение гиперболы, если:
1) расстояние между фокусами равно 10, а расстояние между вершинами 8;
2) действительная полуось равна 5, а эксцентриситет 2,6;
3) расстояние между фокусами равно 10, а эксцентриситет 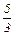 ;
;
4) действительная полуось равна  и гипербола проходит через точку N (-10,4);
и гипербола проходит через точку N (-10,4);
5) расстояние между директрисами равно 4, а расстояние между фокусами 16.
Ответ: 1) 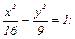 2)
2) 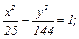
3)  4)
4)  5)
5) 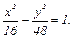
№ 186. Построить линию, записав ее уравнение в каноническом виде:
1) 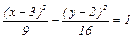 ;
;
2) х2 – 4у2 + 6х + 16у – 11 = 0;
3) ху + 2у – х + 2 = 0.
Ответ: 1) 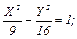 2)
2) 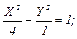 3) XY = - 4.
3) XY = - 4.
№ 187. Определить вид, основные характеристики и построить кривую:
а) 3х2 – 5у2 – 18х + 20у – 8 = 0;
б) 2х2 – у2 – 8х + 6у – 5 = 0;
в) (а – 12)х2 – 4у2 + 4 (а – 12)х – 16у – 16 = 0.
Ответ: 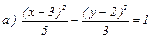 ;
;
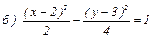 ;
;
 . Рассмотреть 3 случая.
. Рассмотреть 3 случая.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 1383; Нарушение авторских прав?; Мы поможем в написании вашей работы!