Задачи приближения и интерполяции функций и эмпирических данных

Геометрический смысл плохо обусловленных и хорошо обусловленных матриц

Рассмотрим систему уравнений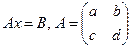

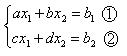
При плохой обусловленности матрицы эти прямые почти параллельны, поэтому любое небольшое возмущение в правой части сказывается на определении точного решения.

Для хорошо обусловленных систем прямые проходят под большим углом, точность решения – высокая.

Задачей приближения или аппроксимации называется задача построения функции, принимающей в заданных точках заданные значения.

Значения функции в заданных точках могут быть представлены в табличной форме и получаются или из экспериментов, или посредством расчета некоторой сложной функции.

Значения функции задаются в системе точек 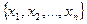– узлы интерполяции.

Каждому узлу интерполяции соответствуют значения функции .

Точное значение функции неизвестно, либо ее вычисление сложно.

Задача заключается в нахождении оценки (аппроксимации) интерполирующей функции .

Форма аппроксимирующей функции известна, не известны параметры .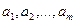

Задача заключается в нахождении этих параметров из условия, что значение аппроксимирующей функции в узлах интерполяции совпадают с известными значениями :

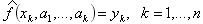
В общем случае – это система нелинейных уравнений относительно .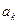

Для того, чтобы она имела решения необходимо, чтобы число уравнений было равно числу неизвестных .

В качестве аппроксимирующей функции используется линейная комбинация линейно-независимых функций, т.е., как правило, аппроксимирующая функция:

.

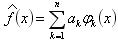Система функций , с помощью которой представляется аппроксимирующая функция, называется базисной функцией (БСФ) или базисом.

В качестве БСФ используются:

1) степенные многочлены: ;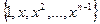

2) тригонометрическая система функций: ;

3) ортогональные между собой многочлены

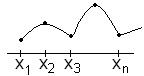
Задача интерполяции заключается в нахождении значений функци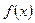и при .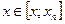

??? 12. Задача интерполяции алгебраическим многочленом с простыми узлами. Формулы Лагранжа и Ньютона. Разделенные разности.

В качестве интерполяционных многочленов может быть использован многочлен Лагранжа, который может быть записан:

Формула Ньютона:

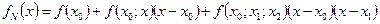
Однако, применение этих формул при использовании интерполяционных многочленов высокого порядка (чем больше порядок многочлена, тем большую точность можно ожидать) сопряжено с большим объемом предварительных вычислений, а также с тем, что эти методы трудно обобщаются на случай функции нескольких переменных.

Более простое решение задач численного дифференцирования достигается с помощью метода неопределенных коэффициентов.

Короткая форма интерполяционной формулы Ньютона для случая равноудаленных узлов:

Рассмотрим последовательность значений функции в узлах интерполяции, она называется разделенной разностью нулевого порядка.

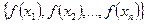
Разделенные разности первого порядка определяется по формуле:

В общем случае:

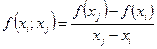
Разделенная разность второго порядка.

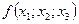– это разделенная разность первого порядка

Таблица разделенных разностей

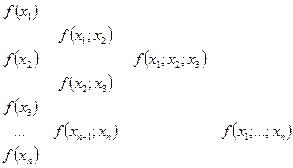
Интерполяционная формула Ньютона с помощью разделенных разностей запишется:

При вычислении многочлена по интерполяционным формулам необходимо учитывать вычислительную сложность алгоритма.

Существуют различные способы вычисления многочлена, которые отличаются по своей вычислительной сложности, т.е. по числу вычислительных операций.

Дата добавления: 2015-04-24