Интегрирование при бесконечных пределах

Метод Гаусса-Кронрода

Недостаток метода Гаусса состоит в том, что он не имеет лёгкого (с вычислительной точки зрения) пути оценки погрешности полученного значения интеграла. Использование правила Рунге требует вычисления подынтегральной функции примерно в таком же числе точек, не давая при этом практически никакого выигрыша точности, в отличие от простых методов, где точность увеличивается в несколько раз при каждом новом разбиении. Кронродом был предложен следующий метод оценки значения интеграла

,

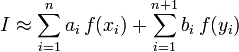где x_i — узлы метода Гаусса по n точкам, а 3 n + 2 параметров a_i, b_i, y_i подобраны таким образом, чтобы порядок точности метода был равен 3 n + 1.

Тогда для оценки погрешности можно использовать эмпирическую формулу:

,

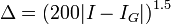где I_G — приближённое значение интеграла, полученное методом Гаусса по n точкам.

Для интегрирования по бесконечным пределам нужно ввести неравномерную сетку, шаги которой нарастают при стремлении к бесконечности, либо можно сделать такую замену переменных в интеграле, после которой пределы будут конечны. Аналогичным образом можно поступить, если функция особая на концах отрезка интегрирования
18. Численное интегрирование методом неопределенных коэффициентов.

В рамках этого метода, производная в точке 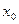ищется в виде линейных комбинаций некоторых функций: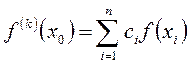

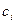– неизвестное

В качестве функции 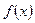берутся многочлены , точки 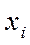– узлы интерполяции.

После подстановки этой функции получим:

Производная в точке :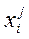

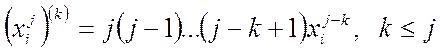
При : .

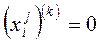Приравнивая значение производной при различных степенях получим систему уравнений:

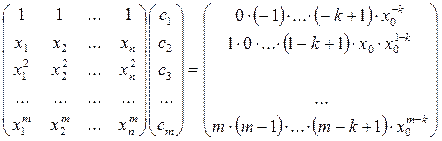
Решения возможны, если .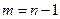

При 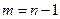определитель матрицы этой системы является определителем Вандермонда, и он отличен он нуля при различных значениях узлов.

Матрица определяется узлами интерполяции, а правая часть представляет собой вектор степеней в узлах, в которых мы оцениваем производную.

Таким образом, всегда можно построить формулу численного дифференцирования с n узлами точную для многочлена степени .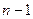

Дата добавления: 2015-04-24