III. Формула прямоугольников, как формула с кратным узлом

II. Формула трапеций

I. Формула прямоугольников

Формулы прямоугольника, трапеций и Симпсона.

Число узлов 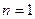, середина интервала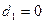

Число узлов 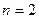, узлы располагаются в точках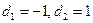

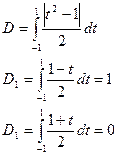
Получим квадратурную формулу:

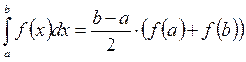
Кратным узлом трапеции называется узел, в котором задается не только значение функции, но и значения некоторого числа его производных.

Интерполяционная функция, в которой используются как значения самой функции, так и значения некоторого числа ее производных, называется формулой Эрмита.

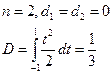
Квадратурная формула принимает вид:

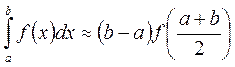
Формула Симпсона получается методом интерполяции при следующих параметрах:

.

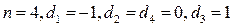21. Ортогональные и ортонормальные системы функций и многочленов. Скалярное произведение. Ортогонализация произвольной системы линейно независимых функций. Формула Грама – Шмидта.

Если 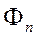– система линейно-независимых функций: 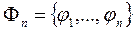, принадлежащих пространству H: 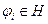, то существует система независимых ортогональных функций: 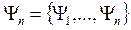, каждая из которых может быть представлена в виде линейной комбинации линейной системы: .

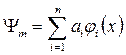Условие ортогонализации: .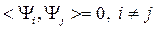

Доказательство:

оно является конструктивным, т.е. основывается на построении алгоритма нахождения ортогональных функций по исходной системе независимых функций.

Первая функция ортогональной системы.

Пусть

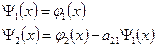
Из условия ортогонализации: ,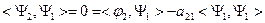

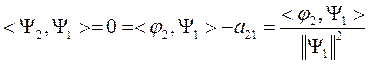
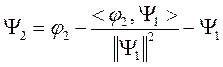
На каком-то шаге получим ортогональные функции: , .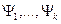

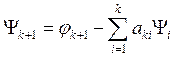Коэффициенты этой линейной комбинации определяются из условия ортогонализации 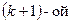функции всем предшествующим функциям системы.

Система функций по условию ортогональна, значит, 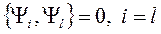, следовательно,

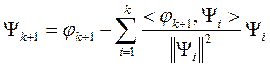
Процедура ортогонализации называется процедурой Грамма-Шмидта.

Все функции выражаются через старую функцию, значит, все функции можно представить в виде линейной комбинации системы функций: .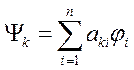

Если представить исходную и ортогональную системы функций в виде векторов:

, ,

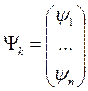то переходы к ортогональной система в матричном виде: .

Матрица B является нижней унитарной матрицей:

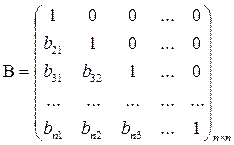
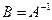
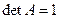
Коэффициенты матрицы A – коэффициенты, полученные в процессе ортогонализации.

При рассмотрении ортогональных многочленов в качестве независимой системы используется система степенных функций:

К ортогональным многочленам относятся многочлены Чебышева первого и второго рода. Ортогональные многочлены легко находятся с помощью рекуррентных формул.

Так многочлены Чебышева первого рода определяются:

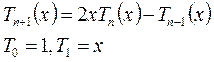
Многочлены Чебышева первого рода являются многочленами ортогональными на интервале с весом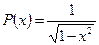

Условие ортогонализации:

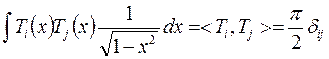
Многочлены Чебышева второго рода можно найти по рекуррентной формуле:

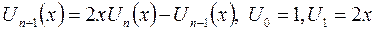
Многочлены Чебышева второго рода являются ортогональными на интервале 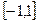с весом .

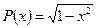Дата добавления: 2015-04-24