Лемма 2

Лемма 1

Тригонометрическая интерполяция и дискретное преобразование Фурье.

Интегрирование быстро осциллирующих функций. Интегрирование функций на больших интервалах изменения аргумента.

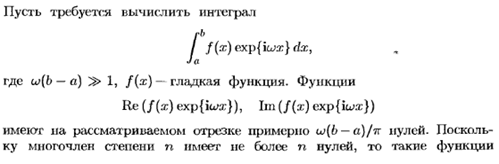
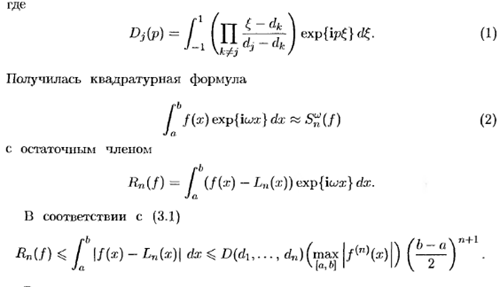
Если 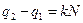, то .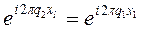

Доказательство:

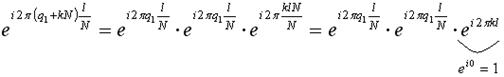
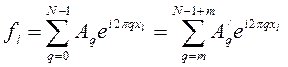
Учитывая лемму 1, значения функции на сетке узлов можно задать с помощью выражения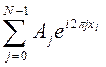

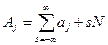
В силу периодичности функции: .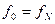

Пусть определено скалярное произведение функций f и g:

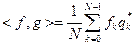
Скалярное произведение функций f и g задается как произведение выборок этих в точках .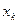

Пусть 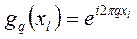– комплексная экспонента в узлах .

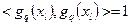
Рассмотрим скалярное произведение функций:

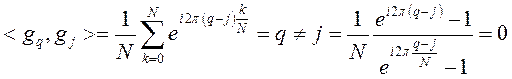
Сумма представляет собой геометрическую прогрессию.

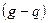– целое число

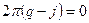
Отсюда следует, что комплексные экспоненты на узлах сетки являются ортонормальными функциями.

Любой периодический сигнал может быть представлен в форме ряда Фурье.

При рассмотрении непериодического сигнала на интервале 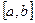, функция 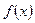продолжается периодическим образом вне этого интервала. Вводится функция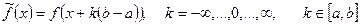

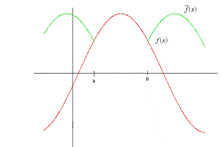В этом случае непериодическая на интервале 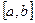функция может быть представлена рядом Фурье периодической функцией .

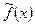Интервал 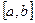посредством преобразования аргумента может быть приведен к интервалу .

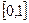Интервал будет считаться интервалом .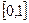

Ряд Фурье непрерывной функции 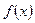на интервале :

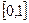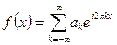
Значение функция на сетке узлов, расположенных с шагом 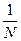записывается:

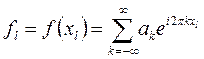
Узлы с шагом 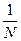делят интервал 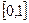на N подинтервалов

В силу периодичности функции: : .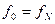

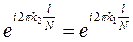Значения функции 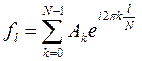. Это выражение называется дискретным рядом Фурье.

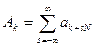
Значения дискретного ряда Фурье совпадают со значениями функции 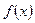на сетке узлов .

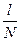Если заменить дискретным рядом Фурье дискретную переменную 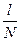на непрерывную переменную, то мы получим функцию 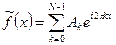, которую можно назвать тригонометрической интерполяционной формулой, функцией 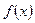, заданной на сетке узлов.

Значения интерполяционной формулы на сетке узлов совпадают со значениями функции 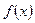: 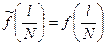. Между узлами сетки эти функции значительно отличаются друг от друга.

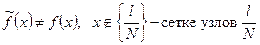
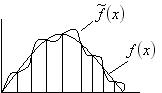Точность приближения интерполяционной формулы зависит от величины шага интерполяции или, по другому, периода дискретизации функции.

Вычисления коэффициентов дискретного ряда Фурье через коэффициенты непрерывного ряда Фурье является дискретной процедурой, т.к. сумма представляет бесконечный ряд.

Более рациональным является определение коэффициентов ряда Фурье, основанное ортогональности экспоненциальных функций.

Отображение множества значений функции на множество коэффициентов дискретного ряда Фурье называется прямым дискретным преобразованием Фурье, а его коэффициенты: .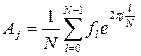

Отображение коэффициентов дискретного ряда Фурье на значения функции в узлах сетки называется обратным дискретным преобразованием Фурье: .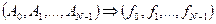

Значения отображения: .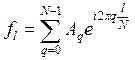
25. Быстрое преобразование Фурье.

С целью умножения числа операций при вычислении дискретного преобразования Фурье (ДПФ) используется быстрое преобразование Фурье (БПФ).

Идея метода БПФ основывается на том, что число N выбирается таким, чтобы оно представляло собой произведение некоторого числа простых чисел: .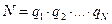

Путем преобразования выражений БПФ число операций сокращается: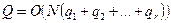

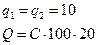
На практике принимается: , ,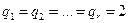

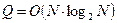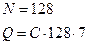
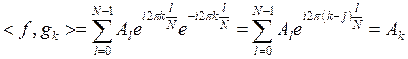
26. Задача наименьших квадратов. Прямой метод решения.

Задача наименьших квадратов, возникающая при научных и инженерных расчетах, может рассматриваться, как задача восстановления зависимости по эмпирическим данным.

Эмпирические данные представляют собой значения неизвестной функции, полученные в результате эксперимента на сетке узлов, в общем случае, неравномерной.

Узлы сетки могут представлять собой моменты времени или пространственные координаты линейной электрической или механической системы.

Координаты узлов и значения функции в этих узлах объединяются в набор точек 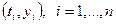, где 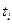– координаты узлов, 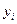– значения функции.

Задача заключается в определении коэффициентов аппроксимирующей функции, которая должна приближать наблюдаемые данные с возможно большей точностью.

Пример: 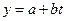. Такая функция часто используется при отслеживании дрейфа временных рядов в экономике.

В общем случае такая функция может не обеспечить требуемую точность восстановления зависимости. Поэтому в качестве аппроксимирующих функций используются общие многочлены по системе линейно-независимых функций:

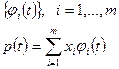
Система независимых функций, которая называется системой, может быть представлена в виде степенных функций, тригонометрических функций и др.

В случае степенных функций .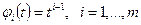

Число базисных функций и размерность пространства базисных функций, как правило, меняет число наблюдаемых данных.

В идеале, желательно, что бы ошибки в узлах сетки имели минимальную величину: .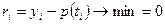

Если потребовать, чтобы ошибки в узлах сетки были равны нулю, то коэффициенты обобщенного многочлена должны удовлетворять матричному уравнению:

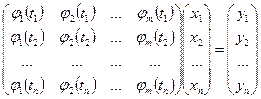
Решения этой системы возможно только при условии, если , и определитель матрицы 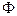отличен от нуля: 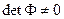, в противном случае решение этой системы оказывается невозможным. Однако, можно подобрать такие значения коэффициентов многочлена, чтобы полученный многочлен приближал наблюдаемые данные к значениям функции.

Точность восстановления зависимости, представленной вектором невязок 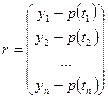можно представить некоторой нормой, которая характеризует среднее значение ошибок по всем узлам.

В качестве нормы можно использовать выражение:

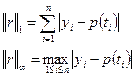
Евклидова норма: 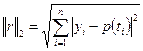или квадрат этой нормы: .

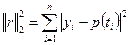Задача наименьших квадратов возникает из задачи минимизации квадрата евклидовой нормы

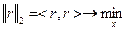
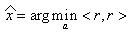
Прямой подход к решению задачи минимизации квадрата евклидовой нормы сводится к нахождению коэффициентов, при которых градиент вектора нормы невязки равен нулю.

Градиент функции обозначается оператором Набла.

Градиент функции – вектор первых частных производных функции по компонентам вектора.

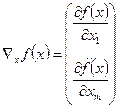
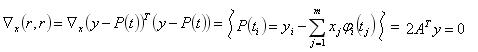
Получим систему линейных алгебраических уравнений:

Решение этой системы сводится к нахождению обратной матрицы:

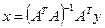
При большой размерности пространства базисных функций, нахождение обратной матрицы является достаточно трудоемкой задачей.

Чтобы преодолеть эту проблему, численные методы решения задачи наименьших квадратов основываются на разложении матриц исходной системы.

Одним из эффективных методов решения задачи является метод QR-разложения.

По этому методу исходная матрица системы уравнений 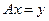разлагается в произведение матриц: .

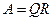Матрица A считается квадратной, если квадратными являются матрицы Q и R.

Матрица Q – ортогональная матрица, а матрица R – верхняя треугольная матрица.

Матрица называется ортогональной, если:

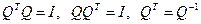
Разложение матрицы A в произведение ортогональной и верхней треугольной матриц позволяет решить алгебраическую систему уравнений в два этапа.

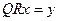
1)

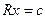
получим систему:

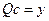
решение системы:

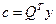
2)

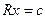
эту систему можно решить методом обратной подстановки.

Дата добавления: 2015-04-24