Отрезок

Взаимное расположение прямых на плоскости. Деление отрезка в данном отношении.

Пучок прямых на плоскости.

Пучок прямых – это совокупность всех тех прямых на плоск-ти, которые проходят через некоторую точку О плоск-ти или параллельны м/у собой. Точка О – центр или носитель Плоскости (Пучка?). Если заданы ур-я двух некоторых прямых плоск-ти:

A ₁ x + B ₁ y + C ₁ = 0 A₂x + В₂у + С₂ =0,

то ур-я Пучка (?!)

l(A ₁ x + B ₁ y + C ₁) +m(A₂x + В₂у + С₂) = 0,

где параметры l и m не обращаются одновременно в нуль и принимают любые значения.

34/ Различные способы задания плоскости в пространстве.

Плоскость - множество точек, равноотстоящих от двух заданных точек.

Положение плоскости в пространстве можно определить:

1. Тремя точками, не лежащими на одной прямой линии.
2. Прямой линией и точкой, не принадлежащей этой прямой.
3. Двумя пересекающимися прямыми.
4. Двумя параллельными прямыми.

35/ Различные способы задания прямой в пространстве.

Прямая линия в линейной алгебре - линия первого порядка.

Общее уравнение прямой: Ах+Ву+С=0

Можно задать:

1.Двумя точками (А и В).

2. Двумя плоскостями (a; b).

3. Двумя проекциями.

4. Точкой и углами наклона к плоскостям проекций.

1) Прямые:

- параллельные - две прямые, которые лежат в одной плоскости и не имеют общих точек.

Проекции параллельных прямых на любую плоскость (не перпендикулярную данным прямым) - параллельны.

- пересекающиеся - две прямые лежащие в одной плоскости и имеющие одну общую точку.

Если прямые пересекаются, то точки пересечения их одноименных проекций находится на одной линии связи.

- скрещивающиеся - две прямые не лежащие в одной плоскости.

Если прямые не пересекаются и не параллельны между собой, то точка пересечения их одноименных проекций не лежит на одной линии связи.

Чтобы некоторый отрезок разделить на эпюре в данном соотношении, надо в том же отношении разделить его проекции.

Если точка М(x; y) лежит на прямой, проходящей через две данные точк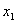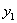и (, ) и (, 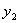), и дано отношение , в котором точка М делит отрезок 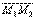, то координаты точки М определяются по формулам

, .

Если точка М является серединой отрезка , то ее координаты определяются по формулам , .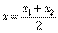

Дата добавления: 2015-04-24