Производная

Поверхности второго порядка.

ПВП — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

a ₁₁ x ² + a ₂₂ y ² + a ₃₃ z ² + 2 a ₁₂ xy + 2 a ₂₃ yz + 2 a ₁₃ xz + 2 a ₁₄ x + 2 a ₂₄ y + 2 a ₃₄ z + a ₄₄ = 0

- цилиндрическая - если для любой точки M ₀ этой поверхности прямая, проходящая через эту точку параллельно образующей 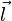, целиком принадлежит поверхности S.

- коническая - если для любой точки M ₀ этой поверхности прямая, проходящая через M ₀ и O, целиком принадлежит этой поверхности.

- пов-ти вращения - если для любой точки M₀(x₀,y₀,z₀) этой поверхности окружность, проходящая через эту точку в плоскости z =z₀ с центром в (0,0,z₀) и радиусом 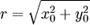, целиком принадлежит этой поверхности.

Производная в математике — функция, являющаяся результатом применения той или иной операции дифференцирования к исходной функции. Физический смысл производной - скорость изменения величины или процесса.

Геометрический смысл производной. На графике функции выбирается абсцисса x0 и вычисляется соответствующая ордината f(x0). В окрестности точки x0 выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая. Расстояние Δx = x — x0 устремляется к нулю, в результате секущая переходит в касательную. Тангенс угла α наклона этой касательной — и есть производная в точке x0.

Если функция 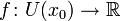имеет конечную производную в точке x0, то в окрестности U(x0) её можно приблизить линейной функцией

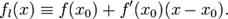
Функция fl называется касательной к f в точке x0. Число f'(x0) является угловым коэффициентом или тангенсом угла наклона касательной прямой.

41/ Интеграл. Геометрические приложения определенного интеграла.

И. – площадь криволинейной трапеции. Процесс нахождения интеграла называется интегрированием.

Существует несколько различных определений операции интегрирования, отличающиеся в технических деталях. Однако все они совместимы, то есть любые два способа интегрирования, если их можно применить к данной функции, дадут один и тот же результат.

Определённый интеграл. Определённый интеграл функции f(x) с нижним пределом a и верхним пределом b определяется в виде разности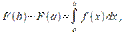

где f(x) определение не состоит в зависимости от того, какая из первообразных используется для вычисления определённого интеграла. Если функция f(x) является непрерывной, то данное определение в случае a<b эквивалентно следующему определению, данному О. Коши: рассматривается произвольное разбиение отрезка [a;b] точками.

Геом. смысл: если f (x) непрерывна и положительна на [ a, b ], то интеграл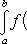

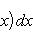
представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f (x).

Дата добавления: 2015-04-24