Основные параметры нормального распределения

Построение нормального распределения по эмпирическому ряду.

Распределение наблюдений.

Правило мажорантности средних.

Нормальное распределение- идеальная модель- теоретически гладкая гистограмма. Идеальный набор данных, в которых большинство чисел сконцентрировано в средней части диапазона значений.

Значения наблюдений не ограничены по своей величине.

ü диапазон ±1 S - 68,26% площади (значений).

ü диапазон ±2 S – 95,44% площади (значений).

ü диапазон ±3 S - 99,72% площади (значений).

Расстояние по горизонтальной оси, измеренное в единицах стандартного отклонения от среднего арифмет-го всегда даёт одинаковую площадь под кривой.

Правосторонняя As > 0; Левосторонняя As < 0

Вероятность того, что имеющее НР случайная величина принимает значение, лежащее в некотором интервале, равна площади под кривой НР между значениями, ограничивающими данный интервал.

Нормальное распределение – непрерывные величины

Характеристики:

1.Среднее или ожидаемое значение дискретной случайной величины X:

2.Стандартное отклонение дискретной случайной величины X (риск, неопределенность ситуации)

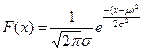Значение наблюдений неограниченны по своей величине

6.3. Показатели формы распределения (центральные моменты, показатели асимметрии, показатель эксцесса).

Моменты распределения. Понятия математического ожидания и дисперсии являются частными случаями более общего понятия для числовых характеристик случайных величин – моментов распределения. Моменты распределения случайной величины вводятся как математические ожидания некоторых простейших функций от случайной величины. Так, моментом порядка k относительно точки х0 называется математическое ожидание М (Х – х0)k. Моменты относительно начала координат х = 0 называются начальными моментами и обозначаются:

Центральные моменты не зависят от начала отсчета значений случайной величины, так как при сдвиге на постоянное значение С ее центр распределения сдвигается на то же значение С, а отклонение от центра не меняется: Х – m = (Х – С) – (m – С).

Дисперсия – это центральный момент второго порядка:

Асимметрия. Центральный момент третьего порядка: служит для оценки асимметрии распределения. Если распределение симметрично относительно точки х = m, то центральный момент третьего порядка будет равен нулю (как и все центральные моменты нечетных порядков). Поэтому, если центральный момент третьего порядка отличен от нуля, то распределение не может быть симметричным. Величину асимметрии оценивают с помощью безразмерного коэффициента асимметрии:

Знак коэффициента асимметрии (18) указывает на правостороннюю или левостороннюю асимметрию (рис. 2).

Эксцесс. Центральный момент четвертого порядка: служит для оценки так называемого эксцесса, определяющего степень крутости (островершинности) кривой распределения вблизи центра распределения по отношению к кривой нормального распределения. Так как для нормального распределения, то в качестве эксцесса принимается величина:

Для нормального распределения Е = 0. Кривые, более островершинные, чем нормальная, имеют положительный эксцесс, более плосковершинные – отрицательный.

Асимметрия.

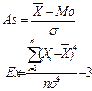Эксцесс

.

Асимметрия НР=0 и Эксцесс=0

Более вытянутая вершина графика эксцесс >0, более пологий график эксцесс<0

Дата добавления: 2015-04-24