Определение

Площадь параллелограмма

Определение.

Периметр параллелограмма

Определение.

Диагональю параллелограмма называется любой отрезок соединяющий две вершины противоположных углов параллелограмма.

Параллелограмм имеет две диагонали - длинную d₁, и короткую - d₂

Формулы определения длины диагонали параллелограмма:

1. формулы диагоналей параллелограмма через стороны и косинус угла β (по теореме косинусов)

d₁ = √a² + b² - 2ab·cosβ

d₂ = √a² + b² + 2ab·cosβ

1. формулы диагоналей параллелограмма через стороны и косинус угла α (по теореме косинусов)

d₁ = √a² + b² + 2ab·cosα

d₂ = √a² + b² - 2ab·cosα

1. формула диагонали параллелограмма через две стороны и известную другую диагональ:

d₁ = √2a² + 2b² - d₂²

d₂ = √2a² + 2b² - d₁²

1. формула диагонали параллелограмма через площадь, известную диагональ и угол между диагоналями:

d1 =	2 S	=	2 S
d2·sinγ	d2·sinδ

d2 =	2 S	=	2 S
d1·sinγ	d1·sinδ

Периметром параллелограмма называется сумма длин всех сторон параллелограмма.

Формулы определения длины периметра параллелограмма:

1. формула периметра параллелограмма через стороны параллелограмма:

P = 2a + 2b = 2(a + b)

1. формула периметра параллелограмма через одну сторону и две диагонали:

P = 2a + √2d₁² + 2d₂² - 4a²

P = 2b + √2d₁² + 2d₂² - 4b²

1. формула периметра параллелограмма через одну сторону, высоту и синус угла:

P =	2(b +	hb	)
sinα

P =	2(a +	ha	)
sinα

Площадью параллелограмма называется пространство ограниченный сторонами параллелограмма, т.е. в пределах периметра параллелограмма.

Формулы определения площади параллелограмма:

1. формула площади параллелограмма через сторону и высоту, проведенную к этой стороне:

S = a · h_a

S = b · h_b

1. формула площади параллелограмма через две стороны и синус угла между ними:

S = ab sinα

S = ab sinβ

1. формула площади параллелограмма через две диагонали и синус угла между ними:

S =		d1d2 sinγ

S =		d1d2 sinδ

Вопрос 3.

Прямоугольник - это четырехугольник у которого две противоположные стороны равны и все четыре угла одинаковы.

Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.

Длинную сторону прямоугольника называют длиной прямоугольника, а короткую - шириной прямоугольника.

Стороны прямоугольника одновременно является его высотами.

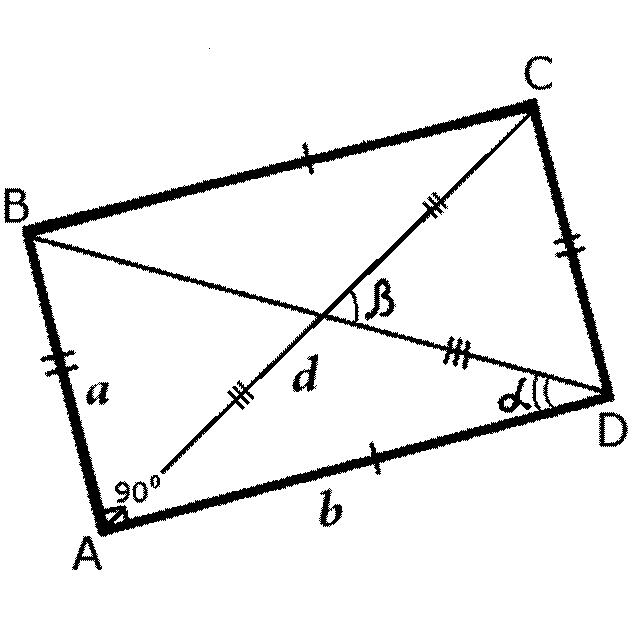
Рис.1		Рис.2

Дата добавления: 2015-04-24