Функции нескольких переменных

32.

31.

Интегрирование по частям

Пусть u (x) и v (x) являются дифференцируемыми функциями. Дифференциал произведения функций u и v определяется формулой Проинтегрировав обе части этого выражения, получим или, переставляя члены, Это и есть формула интегрирования по частям.

Пример 1

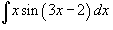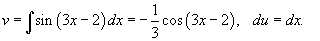Вычислить интеграл . Решение. Используем формулу интегрирования по частям . Пусть . Тогда Следовательно,

33. Формула Ньютона — Лейбница.

Сравнивая формулы площади криволинейной трапеции

и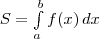

делаем вывод: если F — первообразная для f на [а; b] то

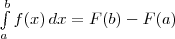(1)

33. Формула (1) называется формулой Ньютона — Лейбница. Она верна для любой функции f, непрерывной на отрезке [а; b

Сформулируем некоторые свойства определенного интеграла в предположении, что подынтегральная функция ограничена на отрезке, по которому она интегрируется.

• Если функция интегрируема на [ a; b ], то она интегрируема на любом отрезке
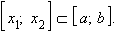
• Для любых a, b и c

• Интеграл обладает свойством линейности: для любых функций f (x) и g (x) и любой постоянной A

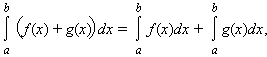
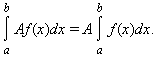
• Если f (x) и g (x) интегрируемы на [ a; b ], то f (x) · g (x) также интегрируема на этом отрезке.
• Если f (x) – периодическая функция с периодом T, то для любого a

34. Замена переменной в определённом интеграле. Теорема. Пусть функция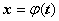

1. определена, непрерывно дифференцируема и монотонна на отрезке ,
2. ,
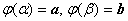3. функция 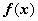непрерывна на отрезке [ a, b ].

Тогда .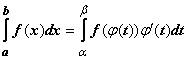

Док-во. Пусть F (x) - первообразная для функции f (x), т.е. 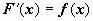, тогда - первообразная для функции . 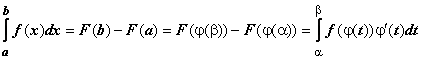, что и требовалось доказать.

При решении задач нельзя забывать о том, что при переходе к новой переменной надо обязательно вычислить новые пределы интеграла.
Пример:

.

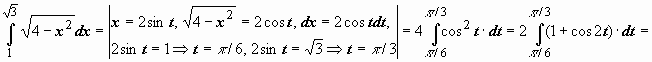
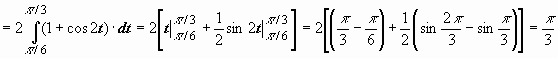35. Теорема 2. Если u (x) и v (x) - две функции, заданные на промежутке [ a, b ] и имеющие там непрерывные производные, то

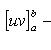
(24)

Формула (24) есть формула интегрирования по частям для определенных интегралов.

Доказательство очень просто. Именно,

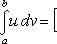
Так как по формуле интегрирования по частям будет

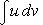
то

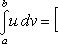
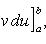
откуда и следует (24).

Пример 1.

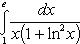
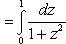
Здесь применена подстановка ln x = z (причем формула (22) прочитывалась слева направо).\

Функции двух переменных

Приращение функции

Функция, дифференцируемая в точке

при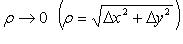

В этом случае дифференциал функции в точке :

- частные производные, вычисленные в точке .

Дифференцирование композиции

1. Если 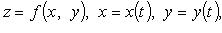то

2. Если 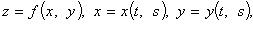то:

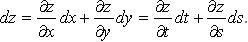
Однородная функция степени k

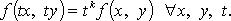
Дата добавления: 2015-04-24