Функциональные ряды

Формально записанное выражение

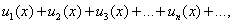(25)

где 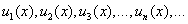- последовательность функций от независимой переменной x, называется функциональным рядом.

Примерами функциональных рядов могут служить:

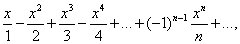(26)

(27)

Придавая независимой переменной x некоторое значение и подставляя его в функциональный ряд (25), получим числовой ряд

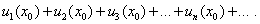
Если он сходится, то говорят, что функциональный ряд (25) сходится при ; если он расходится, что говорят, что ряд (25) расходится при .

41. Степенные ряды Определение

Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом:

Часто рассматривается также ряд, расположенный по степеням (x − x ₀), то есть ряд вида

где x ₀ − действительное число.

Интервал и радиус сходимости

Рассмотрим функцию . Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости.

Если интервал сходимости представляется в виде 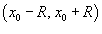, где R > 0, то величина R называется радиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно.
Радиус сходимости можно вычислить, воспользовавшись радикальным признаком Коши, по формуле

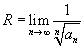
или на основе признака Даламбера:

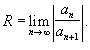
42. Дифференциальные уравнения 1. Основные понятия

Определение. Уравнение вида
F (x, y, y', y'',…, y ⁽ⁿ⁾) = 0, (*)
связывающее аргумент х, функцию у (х) и ее производные, называется дифференциальным уравнением n -го порядка.
Определение. Общим решением дифференциального уравнения n -го порядка называется функция у = φ(х, С ₁ ,С ₂ ,…,С_n), которая зависит от аргумента х и n независимых произвольных постоянных С ₁, С ₂, …, С_n, обращающая вместе со своими производными у', у'',…, у ⁽ⁿ⁾ уравнение (*) в тождество.
Определение. Частным решением уравнения (*) называется решение, которое получается из общего решения, если придавать постоянным С ₁, С ₂, …, С_n определенные числовые значения.

Уравнения с разделяющимися переменными

Самым простым примером уравнения первого порядка является уравнение с разделяющимися переменными.

Дифференциальное уравнение , допускающее запись в виде

,

а также уравнение в дифференциалах, которое можно записать в форме

называются уравнениями с разделяющимися переменными.

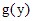Предполагается, что функция определена и непрерывна на отрезке , а функция определена и непрерывна на отрезке . Для решения такого уравнения надо обе его части умножить или разделить на такое выражение, чтобы в одну часть уравнения входило только в другую – только 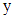, а затем проинтегрировать обе части.

При делении обеих частей уравнения на выражение, содержащее и 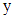могут быть потеряны решения, обращающие это выражение в нуль.

43. 2. Линейные дифференциальные уравнения первого порядка

Определение. Уравнение вида y'+ ρ(x) y=f (x), где ρ(x) и f (x) непрерывные функции, называется линейным дифференциальным уравнением первого порядка.
Пример. Найти общее решение уравнения y'+ 3 y=e ^{2 x} и частное решение,удовлетворяющее начальным условиям х =0, у =1.
Решение. Данное уравне

ние является линейным.
Здесь ρ(x)=3 и f (x)= e ^{2 x} .
Решение ищем в виде y=U ∙υ, где U и υ – некоторые функции от х. Находим y'= U' υ+ U υ ' и подставляем в уравнение значение y и y', получаем: U' υ +U υ ' +3 U υ= e ^{2 x} или U' υ +U (υ ' +3υ)= e ^{2 x} .
Найдем одно значение υ, при котором выражение в скобках, обращается в нуль: υ ' +3υ=0. Получим уравнение с разделяющимися переменными. Решая его получаем: 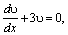ln υ =–3 x,υ= e ^{–3 x} .
Подставляем найденное значение υ в исходное дифференциальное уравнение, получаем уравнение с разделяющимися переменными:
.
Итак, общее решение данного уравнения имеет вид:
.
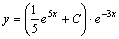Найдем частное решение. Для этого подставим начальные условия в выражение для общего решения и найдем С.
.
Частное решение имеет вид: .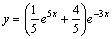

Дата добавления: 2015-04-24