Вопрос № 5. Определения операций над множествами (объединение , пересечение , разность ). Понятие универсального множества, операция дополнения

Вопрос № 3. Высказывания, зависящие от параметра (предикаты). Примеры. Высказывания, содержащие кванторы общности и существования. Примеры таких высказываний. Отрицание высказываний, содержащих кванторы (формальная конструкция и её смысл).

Предикат – это то, что утверждается или отрицается о субъекте суждения.

Пр.: пусть Х›5

А(Х): Х›5

А(1): 1›5 – ложь, 8›5 – истина

Кванторы – логические символы, к-ые обозначают операции, ограничивающие мн-во истинности предиката.

Кв-р общности(∀) – каждый, любой, всякий

Кв-р существования(∃) – сущ-ет по крайней мере один

Правила отрицания кванторов

(∀ х) = (∃х) Р(х)

(∃х) Р(х) = (∀х) Р(х)

Примеры высказываний с кванторами:

1) х –одноклассник (Х – весь класс)

А(х): х поступили в ВУЗ

∃(х): А(х) – найдётся хотя бы один однокл, к-ый поступил в ВУЗ

2) А(Х), х∊Х(х∊ множ-ву параметров),∀х: А(х) (Для каждого х из Х выск.А(х)-истинно)

Отрицание высказываний с кванторами:

∀⇒∃; ∃⇒∀;

Пр.: В: (∀х: А(х)); В: (∃Х:АХ)

Вопрос № 4. Понятие множества (по Кантору), символ принадлежности 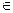, пустое множество. Способы задания множеств. Примеры множеств, заданных различными способами. Равенство множеств, определение подмножества, символ включения 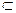, понятие несобственного подмножества. Примеры.

Множество (по Кантору) – многое, мыслимое как единое.

Элементы мн-ва – объекты, составляющие это мн-во.

Способы задания мн-в

1) Перечислением своих элементов: А=[a, b, c,…]

2) Через описание ограничительного св-ва. А=[х| Р(х)]- А мн-во таких элементов х, к-ые обладают св-ом Р(х).

Принадлежность(∊) – элем-т х явл. эл-ом мн-ва А

Пустое мн-во(∅) – мн-во, не содержащее ни одного эл-та.

Равенство мн-в – мн-ва А и В равны, если они состоят из одних и тех же эл-тов.

Подмн-во – подмн-во В наз.подмн-ом А, если все эл-ты мн-ва В принадлежат мн-ву А.

Включение (⊂) – если каждый эл-т х мн-ва Х явл.эл-ом мн-ва У, то говорят, что мн-во Х содержится во мн-ве У.

Несобственное подмн-во – когда непустое подмн-во В совпадает с мн-ом А.

Дата добавления: 2015-04-24