Послідовність. Границя послідовності

Елементарні функції.

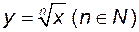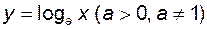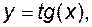
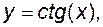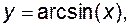
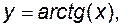
Означення. Основні елементарні функції: степенева , показникова , обернена до степеневої , логарифмічна , тригонометричні обернені тригонометричні а також функції, знайдені за допомогою формул, що містять скінчене число арифметичних дій (додавання, віднімання, множення, ділення) і суперпозицій основних елементарних функцій, називаються елементарними функціями.

З основними елементарними функціями ми познайомились в шкільному курсі математики, а тому їх властивості пропонуємо розглянути самостійно.

Функція, задана на множині натуральних чисел, називається числовою послідовністю.

Позначається 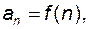де – загальний член послідовності. Кожна числова послідовність вважається заданою, якщо вказано правило чи закон її утворення.

Наприклад, нехай задано загальний член послідовності 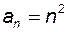, тоді її членами будуть числа 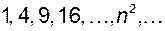. Для послідовностей з загальними членами 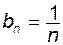, членами будуть відповідно числа: та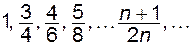

Приклад 2.1. Побудувати числову послідовність для знаходження грошових накопичень з урахуванням складних процентів.

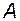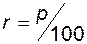Розв'язок. Нехай початкова сума вкладу складає грн., процентна ставка дорівнює річних. Величина називається питомою процентною ставкою.

На кінець першого року сума вкладу складе , на кінець другого року – 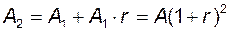, на кінець року – .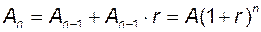

Розглянемо послідовності і 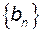. Побудуємо точки на числовій осі, що відповідають членам цих послідовностей:

З рисунку видно, що члени послідовності 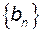по мірі зростання номера 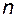наближаються до точки 0, члени другої послідовності необмежено віддаляються від початку координат.

Виберемо - окіл точки 0 з 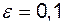. Поза цим околом знаходяться десять перших членів, всі інші, тобто всі починаючи з номера 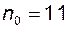, належать цьому околу. Виберемо менший окіл точки 0, наприклад 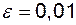. Поза цим околом знаходяться перші сто членів, а всі інші, починаючи з номера 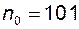, належать вибраному околу.

Означення 1. Число 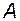називається границею числової послідовності , якщо будь-який - окіл точки 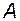містить всі члени послідовності, починаючи з деякого номера 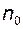, а поза ним знаходиться фіксоване число членів послідовності.

Якщо члени послідовності належать - околу точки 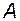, то це значить, що для всіх цих членів виконується нерівність 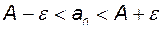, або згідно властивості 7 модуля .

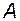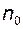Означення 2. Число називається границею числової послідовності , якщо для будь-якого існує такий номер , що для всіх членів послідовності з номерами 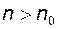виконується нерівність

. (2.1)

Границя числової послідовності позначається 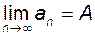або .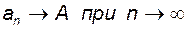

Приклад 2.2 Довести, що для послідовності , .

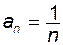
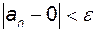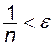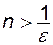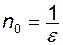Розв'язування. Для будь-якого нерівність (2.1) або виконується при . Отже, при будь-якому існує такий номер (або рівний цілій частині 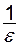), що для всіх 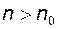виконується нерівність 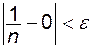. А це означає, що .

Приклад 2.3 Довести, що послідовність 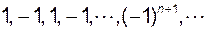не має границі.

Розв’язування. При будь-якому 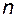два сусідні члени цієї послідовності відрізняються за модулем на 2. Отже для 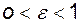на числовій осі не має жодної точки - окіл якої містив би усі члени послідовності починаючи з деякого 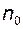. Це означає, що ні одне дійсне число не може бути границею цієї послідовності.

Послідовності, які мають границю, називаються збіжними, а ті що не мають – розбіжними.

Обмежені послідовності. Зв'язок між існуванням границі та її обмеженістю.

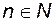Означення. Послідовність називається обмеженою, якщо існує таке число , що для всіх виконується нерівність .

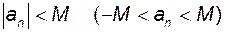Теорема. Якщо послідовність має границю, то вона обмежена.

Доведення. Нехай 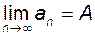. Для існує номер такий номер 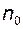, що для всіх членів послідовності з номерами 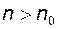виконується нерівність 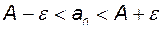. Виберемо 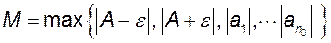. Тоді для всіх 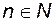виконується нерівність 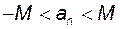, а отже послідовність є обмеженою.

Зауважимо, що протилежне твердження в цілому не вірне. Наприклад, послідовність 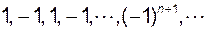обмежена, але границі не має.

Дата добавления: 2015-05-24