Класифікація та деякі властивості функцій

Складена функція.

Завдання для самостійного розв’язування.

1.1 Знайти область визначення функцій:

а) ; б) ;

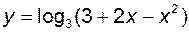в) ; г) ;

Відповіді:

1.1 а) б)

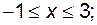в) г)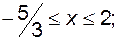

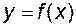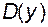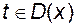Нехай функція визначена на множині , а функція на множині , причому для всіх відповідне значення 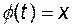належить множині 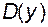. Тоді на множині визначена функція , що називається складеною функцією від 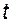, або суперпозицією функцій і .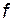

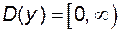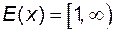Наприклад, функція визначена на множині , а функція визначена на множині і має область зміни . Так як множина , то суперпозиція цих функцій визначена на множині .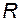

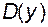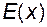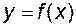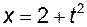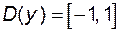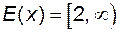Проте може статись так, що і не мають спільних точок, тоді відповідні функції і не утворюють суперпозицію. Наприклад, функції і такі, що і не мають ні однієї спільної точки. Таким чином, вираз 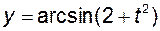не задає функції від .

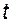В багатьох випадках знання особливостей функцій допомагає побудувати їх графіки. Розглянемо деякі типи функцій.

Означення. Функція 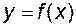, визначена на множині 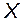, називається обмеженою на цій множині, якщо існує таке число , що для всіх 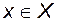виконується нерівність .

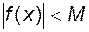Протилежне поняття формулюється так:

Означення. Функція 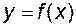називається не обмеженою на множині 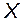, якщо для будь-якого , існує таке, що виконується нерівність .

Графік обмеженої функції розміщується між двома прямими, паралельними осі 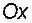: 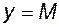та .

Означення. Функція 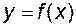, визначена на проміжку 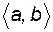, називається зростаючою (неспадною, спадною, незростаючою) на цьому проміжку, якщо для всіх 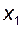і з цього проміжку, що задовольняють нерівності 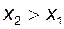виконується нерівність (, , ).

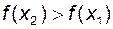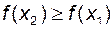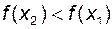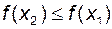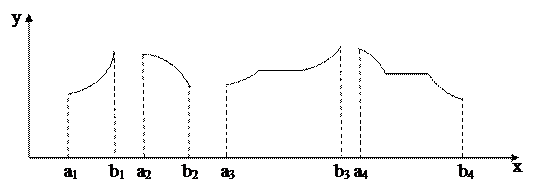
Зростаючі, спадні, неспадні та незростаючі функції називаються монотонними, а зростаючі і спадні, крім того називають строго монотонними. Графіки цих функцій зображені на рис.1

Рис.1.

Означення. Функція 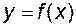, визначена на множині 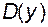, розміщеній симетрично відносно початку координат, називається парною (непарною), якщо для виконується рівність ().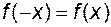

Графік парної функції симетричний відносно осі 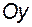(Рис.2), а графік непарної функції – симетричний відносно початку координат (Рис.3). Ця особливість графіків парної та непарної функцій дає змогу скоротити роботу з побудовою графіків таких функцій: досить побудувати графік функції тільки в правій півплощині.

Рис.2 Рис.3

Дата добавления: 2015-05-24