Розриву

Властивості. Розривні функції. Класифікація точок

Означення. Функція 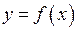називається неперервною на множині , якщо вона неперервна у будь якій точці множини .

Зокрема, функція 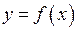неперервна на відрізку 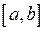, якщо вона неперервна у кожній точці відрізка 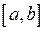, тобто і у точках 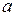і 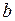. І функція 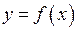неперервна на інтервалі 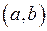, якщо вона неперервна у кожній точці інтервалу 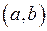, тобто у точках 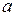і 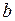неперервності може і не бути. І ця, на перший погляд, незначна відмінність породжує суттєву різницю у властивостях функцій, неперервних на відрізку, і функцій, неперервних на інтервалі або півінтервалі. Ці властивості ми сформулюємо у вигляді декількох теорем. Доведення цих теорем вимагає методів, які виходять за межі нашого курсую тому ми їх наведемо без доведення*.

Перша теорема Вейєрштрасса*. Якщо функція 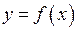визначена і неперервна на відрізку 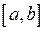, то вона обмежена на цьому відрізку.

З геометричної точки зору це твердження означає, що графік неперервної на відрізку функції цілком міститься всередині деякого прямокутника (рис. 38).

Рис. 38

Твердження теореми втрачає силу, якщо відрізок замінити інтервалом, або півінтервалом. Наприклад, функція 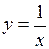неперервна на інтервалі 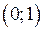, але не є на ньому обмеженою, оскільки .

Друга теорема Вейєрштрасса. Якщо функція 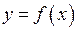визначена і неперервна на відрізку 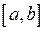, то вона досягає на цьому відрізку свого найбільшого та найменшого значень.

Знову ж твердження теореми втрачає силу, якщо відрізок замінити інтервалом, або півінтервалом. Наприклад, найменше значення функції на інтервалі 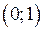дорівнює нулю, а найбільше дорівнює 1, але ці значення досягаються лише у точках відповідно 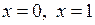, які до інтервалу не входять.

Перша теорема Больцано**– Коші (теорема про корінь). Нехай функція 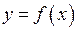визначена і неперервна на відрізку 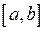і в точках 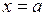і набуває значень різних знаків. Тоді на інтервалі 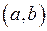існує принаймні одна точка така. що .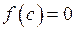

Геометричну ілюстрацію теореми наведено на рис. 39.

Рис. 39

Тобто якщо суцільна лінія з нижньої півплощини проходить у верхню, або навпаки, вона обов’язково у деякій точці перетинає вісь .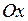

Точка 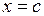називається коренем рівняння 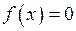. Сформульована теорема тільки стверджує існування кореня, але не вказує, як його знайти. тем не менш, використовуючи цю теорему, можна знайти корінь наближено.

Розглянемо приклад.

Довести, що на відрізку 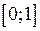рівняння 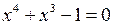має корінь, і знайти цей корінь з точністю 0,1.

Нехай . Ця функція неперервна на всій числовій прямій, отже і на відрізку 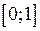. Оскільки 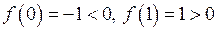, то за першою теоремою Больцано–Коші на відрізку 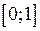дане рівняння має корінь. Поділимо точкою 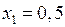відрізок 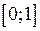навпіл і з двох отриманих відрізків і 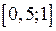оберемо той, на кінцях якого функція 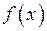набуває значень різних знаків. Оскільки , то це відрізок 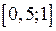. Отже знову за тою ж теоремою на ньому є корінь нашого рівняння. Далі точкою 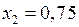ділимо цей відрізок навпіл і знову з двох отриманих відрізків 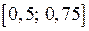і 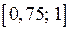обираємо той, на кінцях якого функція набуває значень різних знаків. Оскільки , то це відрізок 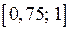. Продовжуючи цей процес, далі знаходимо: ; . Обираємо далі відрізок . Довжина цього відрізку 0,875-0,75=0,125. 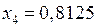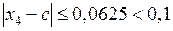Отже, якщо у якості наближеного значення кореня взяти точку , яка ділить відрізок навпіл, то отримаємо: , тобто необхідну точність досягнено. Отже 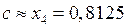. Значення функції 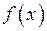у цій точці: .

Продовжуючи цей процес, можна знайти корінь з будь якою наперед заданою точністю. Але навіть з цього прикладу можна помітити, що для досягнення точності 0,1 ми змушені зробити 4 кроки. А більшість прикладних задач вимагає значно вищої точності. Припустимо, що нам треба знайти корінь з деякою точністю . Тоді неважко переконатися, що кількість кроків 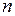, яка необхідна для досягнення цієї точності, повинна задовольнять нерівність:

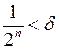, тобто 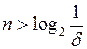. Наприклад, для досягнення точності 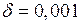треба зробити 10 кроків. Тому на практиці частіше використовують інші, більш потужні методи знаходження коренів рівнянь, наприклад, метод Ньютона (див., напр., посібник [1], стор.268–271).

Дата добавления: 2015-05-24