
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нескінченно малі функції та їх властивості
Спробуємо тепер означення границі послідовності, яке було дано у лекції 3, узагальнити на випадок функції  . Візьмемо деяку послідовність
. Візьмемо деяку послідовність 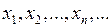 значень аргумента
значень аргумента 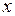 , яка збігається до числа
, яка збігається до числа  , тобто
, тобто  . Тоді відповідно значення функції
. Тоді відповідно значення функції  також будуть утворювати деяку послідовність
також будуть утворювати деяку послідовність 
Означення. Число 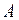 називається границею функції
називається границею функції  при
при  (або у точці
(або у точці  ), якщо для будь якої послідовності
), якщо для будь якої послідовності  значень аргумента
значень аргумента 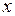 , такої, що
, такої, що 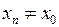 , і
, і  , відповідна послідовність значень функції
, відповідна послідовність значень функції  збігається до числа
збігається до числа 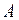 , тобто
, тобто 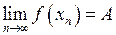 .
.
У цьому випадку ми пишемо:
 .
.
Наведене означення називається означенням функції на мові послідовностей, або означенням Гейне. *
Існує ще одне означення границі функції, яке полягає у наступному. В лекції 3 ми інтуїтивно ввели поняття границі функції, як деякого числа 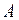 , до якого «наближаються» (або, як кажуть у математиці, прямують) значення функції
, до якого «наближаються» (або, як кажуть у математиці, прямують) значення функції  , якщо значення аргумента
, якщо значення аргумента 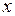 «наближаються» (прямують) до числа
«наближаються» (прямують) до числа  . Оскільки у нас з’явилися терміни «наближаються», «близько», треба ввести деяку міру цієї близькості, а саме міру близькості аргумента
. Оскільки у нас з’явилися терміни «наближаються», «близько», треба ввести деяку міру цієї близькості, а саме міру близькості аргумента 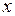 до числа
до числа  і значення функції
і значення функції  до числа
до числа 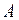 . Позначимо першу з цих мір через
. Позначимо першу з цих мір через  . Це буде означати, що
. Це буде означати, що
 , (*) тобто значення аргумента
, (*) тобто значення аргумента 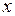 потрапляють в
потрапляють в  -окіл точки
-окіл точки  . Другу з цих мір позначимо через
. Другу з цих мір позначимо через  . Це буде означати, що
. Це буде означати, що
 , (**) тобто значення функції
, (**) тобто значення функції  потрапляють в
потрапляють в  -окіл точки
-окіл точки 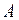 . за рахунок чого може здійснитися друга нерівність? Очевидно, за рахунок достатнього ступеня близькості
. за рахунок чого може здійснитися друга нерівність? Очевидно, за рахунок достатнього ступеня близькості 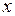 до
до  , і цей ступінь близькості, очевидно, повинен залежати від
, і цей ступінь близькості, очевидно, повинен залежати від  . Іншими словами по заданому числу
. Іншими словами по заданому числу  ми повинні знайти число
ми повинні знайти число  , яке залежить від
, яке залежить від  , таке, що виконання нерівності (*) забезпечує і виконання нерівності (**). Саме цей факт виражає наступне означення.
, таке, що виконання нерівності (*) забезпечує і виконання нерівності (**). Саме цей факт виражає наступне означення.
Означення. Число 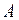 називається границею функції
називається границею функції  при
при  (або у точці
(або у точці  ), якщо для кожного додатного числа
), якщо для кожного додатного числа  існує таке додатне число
існує таке додатне число  , яке залежить від
, яке залежить від  , що для будь яких значень
, що для будь яких значень 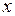 , що задовольняють нерівність
, що задовольняють нерівність  , а також
, а також 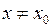 , виконана нерівність
, виконана нерівність  .
.
У цьому випадку пишемо:  .
.
У символьній формі запису це означення має такий вид:
 .
.
Саме таку форму ми будемо використовувати у подальшому.
Наведене означення називається означенням границі функції на мові  , або означенням Коші*. Геометрична його ілюстрація наведена на рис. 30. З нього видно, що якщо значення аргумента
, або означенням Коші*. Геометрична його ілюстрація наведена на рис. 30. З нього видно, що якщо значення аргумента 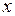 належать множині
належать множині 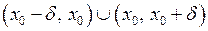 , тобто
, тобто 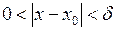 , то значення функції
, то значення функції  належать проміжку
належать проміжку  , тобто
, тобто  .
.

Рис. 30
Приклади.
1. Доведемо, що  . Використаємо означення Коші. Задамо довільне
. Використаємо означення Коші. Задамо довільне  і розглянемо:
і розглянемо:

 .
.
Нехай тепер  . Тоді
. Тоді  . Вимагатимемо, щоб останній вираз був менше, ніж
. Вимагатимемо, щоб останній вираз був менше, ніж  (тоді
(тоді 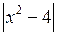 тим більш буде менше, ніж
тим більш буде менше, ніж  ), тобто
), тобто  . Розв’язком цієї квадратної нерівності (враховуючи, що
. Розв’язком цієї квадратної нерівності (враховуючи, що  ) є інтервал
) є інтервал  . Таким чином, якщо ми оберемо
. Таким чином, якщо ми оберемо 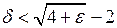 (тобто по заданому
(тобто по заданому  знайшли
знайшли  ), то забезпечимо виконання нерівності
), то забезпечимо виконання нерівності  . У якості
. У якості  можна взяти будь яке число з інтервалу
можна взяти будь яке число з інтервалу  , наприклад
, наприклад  .
.
2. Доведемо, що  .
.
Знову використаємо означення Коші. Задамо довільне  і розглянемо
і розглянемо  :
:
 .
.
Якщо  , то, обираючи
, то, обираючи  (наприклад
(наприклад  ), забезпечуємо виконання нерівності
), забезпечуємо виконання нерівності  , що й треба було встановити.
, що й треба було встановити.
3. Доведемо, що функція  не має ніякої границі при
не має ніякої границі при 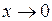 . Скористаємось тепер означенням Гейне. Розглянемо послідовність
. Скористаємось тепер означенням Гейне. Розглянемо послідовність  , де
, де 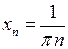 . Очевидно, що
. Очевидно, що  . В той же час:
. В той же час: 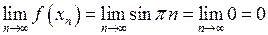 .
.
Тепер розглянемо іншу послідовність  , де
, де  . Знову
. Знову 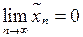 . Але цього разу
. Але цього разу  .
.
Отже, для двох різних послідовностей значень аргумента, прямуючих до нуля, відповідні послідовності значень функції мають різні границі – 0 і 1. І тоді, згідно з означенням Гейне, наша функція не має границі при 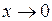 .
.
Можна довести, що означення границі функції по Коші і по Гейне еквівалентні (див., напр.., [2, стор. 145–146]).
У лекції 3 ми вже відмічали, що не слід змішувати поняття границі функції  у точці
у точці  і значення функції у цій точці. Саме тому в означенні границі функції є суттєва умова: треба, щоб було
і значення функції у цій точці. Саме тому в означенні границі функції є суттєва умова: треба, щоб було 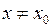 ; або, що те ж саме,
; або, що те ж саме,  . Приклад 2 показує, що границя може існувати і тоді, коли функція взагалі не визначена у точці
. Приклад 2 показує, що границя може існувати і тоді, коли функція взагалі не визначена у точці  , Але, навіть у тому випадку, коли функція визначена у точці
, Але, навіть у тому випадку, коли функція визначена у точці  , її границя у цій точці зовсім не обов’язково дорівнює значенню функції у цій точці. Розглянемо детальніше приклад з лекції 3.
, її границя у цій точці зовсім не обов’язково дорівнює значенню функції у цій точці. Розглянемо детальніше приклад з лекції 3.

Доведемо, що  . Задамо
. Задамо  і розглянемо для будь яких
і розглянемо для будь яких  :
:
 , тобто у якості
, тобто у якості  можна взяти будь яке додатне число. Разом з цим
можна взяти будь яке додатне число. Разом з цим  .
.
Може бути і така ситуація, коли функція визначена у точці  , а границі функції у цій точці не існує. Розглянемо, наприклад, функцію:
, а границі функції у цій точці не існує. Розглянемо, наприклад, функцію:

Ця функція визначена у точці  , а границі у цій точці не існує (див. приклад 3).
, а границі у цій точці не існує (див. приклад 3).
В наведених означеннях границі функції значення аргумента 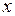 прямувало до скінченого числа
прямувало до скінченого числа  . Але ці значення можуть прямувати і до нескінченності (саме така ситуація спостерігається, наприклад, тоді, коли у якості функції розглядається послідовність). Тоді означення функції приймає наступний вид:
. Але ці значення можуть прямувати і до нескінченності (саме така ситуація спостерігається, наприклад, тоді, коли у якості функції розглядається послідовність). Тоді означення функції приймає наступний вид:
Означення. Число 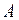 називається границею функції
називається границею функції  при
при  , якщо для будь якого числа
, якщо для будь якого числа  існує таке число
існує таке число  , що нерівність
, що нерівність  гарантує виконання нерівності
гарантує виконання нерівності  .
.
Тоді пишемо:
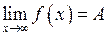 .
.
Це означення за змістом близько до означення границі послідовності, тому особливих пояснень не вимагає.
Сама границя функції теж може бути нескінченною.
Означення. Кажуть, що границя функції  при
при  дорівнює нескінченності, якщо для будь якого додатного числа
дорівнює нескінченності, якщо для будь якого додатного числа 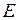 існує таке додатне число
існує таке додатне число  , що виконання нерівності
, що виконання нерівності 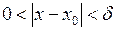 гарантує виконання нерівності
гарантує виконання нерівності  .
.
Тоді пишемо:  .
.
Тобто за рахунок достатньої близькості аргумента 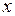 до числа
до числа  значення функції
значення функції  може бути зроблено за модулем більшим, ніж будь яке наперед задане число
може бути зроблено за модулем більшим, ніж будь яке наперед задане число 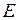 .
.
У цьому випадку функція  називається нескінченно великою у точці
називається нескінченно великою у точці  .
.
Приклад. Довести, що функція 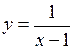 є нескінченно великою у точці
є нескінченно великою у точці  .
.
Задамо довільне  і розглянемо:
і розглянемо:
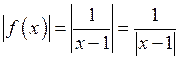 .
.
Якщо  , то
, то  .
.
Вимагатимемо, щоб 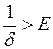 , тобто
, тобто  . Наприклад, можна взяти
. Наприклад, можна взяти  . Тоді за даним
. Тоді за даним 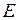 ми знайшли
ми знайшли  таке, що з нерівності
таке, що з нерівності  випливає нерівність
випливає нерівність  , тобто
, тобто  .
.
Границя функції може дорівнювати не просто нескінченності, а нескінченності з певним знаком.
Означення. Кажуть, що  , якщо
, якщо  .
.
Наприклад:  .
.
Завдання. Самостійно сформулюйте означення того що функція  має нескінченну границю при
має нескінченну границю при  , тобто
, тобто 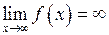 .
.
Теорема. Якщо функція  має границю при
має границю при  , то ця границя єдина.
, то ця границя єдина.
Доведення. Припустимо, що функція  у точці
у точці  має дві границі
має дві границі 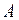 і
і  , причому
, причому 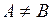 . Тоді
. Тоді  . Оскільки
. Оскільки  , то
, то  . А оскільки також
. А оскільки також 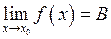 , то
, то  . Позначимо
. Позначимо  . Тоді, якщо
. Тоді, якщо 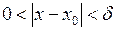 , то будуть водночас виконуватись нерівності
, то будуть водночас виконуватись нерівності  . Оскільки ці нерівності виконуються для будь якого додатного
. Оскільки ці нерівності виконуються для будь якого додатного  , то покладемо, наприклад,
, то покладемо, наприклад,  . Тоді матимемо:
. Тоді матимемо:

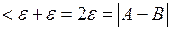 , тобто додатне число
, тобто додатне число  менше самого себе, що неможливо. Отже функція може мати у даній точці лише одну границю.
менше самого себе, що неможливо. Отже функція може мати у даній точці лише одну границю.
З поняттям границі функції тісно пов’язано поняття нескінченно малої функції.
Означення. Функція  називається нескінченно малою при
називається нескінченно малою при  , якщо
, якщо  .
.
Тобто, якщо 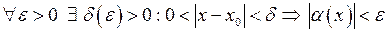 .
.
Аналогічно визначаються функції, нескінченно малі при  .
.
Наприклад, функція 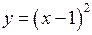 – нескінченно мала при
– нескінченно мала при 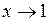 ,
,  – нескінченно мала при
– нескінченно мала при 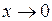 , а
, а 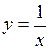 – нескінченно мала при
– нескінченно мала при  .
.
Теорема. Якщо функції  та
та  нескінченно малі при
нескінченно малі при  , то функції
, то функції 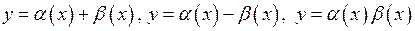 – також нескінченно малі при
– також нескінченно малі при  .
.
Доведення. Доведемо це твердження лише для суми функцій (для різниці та добутку доводиться аналогічно, зробіть це самостійно). Отже, оскільки  – нескінченно мала при
– нескінченно мала при  , то
, то 
 . А оскільки
. А оскільки  – нескінченно мала при
– нескінченно мала при  , то
, то 
 . Якщо тепер покласти
. Якщо тепер покласти  , то з нерівності
, то з нерівності 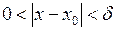 буде випливати, що водночас
буде випливати, що водночас 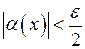 і
і  . Тоді
. Тоді
 , а це й означає що функція
, а це й означає що функція  – нескінченно мала при
– нескінченно мала при  .
.
Звідси, зокрема, випливає, що сума скінченого числа нескінченно малих функцій є функція нескінченно мала..
Зауваження. Частка двох нескінченно малих функцій не обов’язково функція нескінченно мала. Наведемо приклад. Розглянемо функції 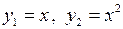 . Обидві ці функції нескінченно малі при
. Обидві ці функції нескінченно малі при 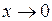 . Але
. Але  не є нескінченно малою при
не є нескінченно малою при 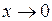 .
.
Теорема. Добуток обмеженої функції на нескінченно малу є функція нескінченно мала.
Доведення. Нехай функція  обмежена при
обмежена при  , а функція
, а функція  – нескінченно мала при
– нескінченно мала при  . Тоді у деякому
. Тоді у деякому  -околі точки
-околі точки  виконується нерівність
виконується нерівність  , де
, де  . Крім того
. Крім того 
 . Якщо тепер
. Якщо тепер  , то матимемо:
, то матимемо:
 , тобто
, тобто  – нескінченно мала при
– нескінченно мала при  .
.
Зокрема, добуток нескінченно малої функції на сталу є функція нескінченно мала.
Теорема. Якщо функція  – нескінченно мала при
– нескінченно мала при  , то функція
, то функція  – нескінченно велика при
– нескінченно велика при  . І навпаки, якщо функція
. І навпаки, якщо функція  нескінченно велика при
нескінченно велика при  , то функція
, то функція  – нескінченно мала при
– нескінченно мала при  .
.
Доведення. Нехай 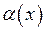 – нескінченно мала при
– нескінченно мала при  . Тоді
. Тоді 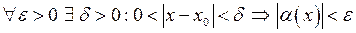 . Задамо довільне
. Задамо довільне  . Розглянемо при
. Розглянемо при 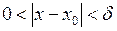 :
:
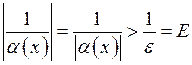 , якщо обрати
, якщо обрати  . Це й означає, що функція
. Це й означає, що функція  – нескінченно велика при
– нескінченно велика при  .
.
Друга частина твердження доводиться аналогічно.
Лекція 7. Основні теореми про границі функцій. Перша
|
|
Дата добавления: 2015-05-24; Просмотров: 2771; Нарушение авторских прав?; Мы поможем в написании вашей работы!