Деякі важливі типи функцій

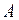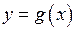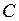Визначимо тепер операції над функціями. Нехай маємо функцію , яка визначена на множині , і функцію , яка визначена на множині . Припустимо, що . Тоді на множині можна визначити суму функцій . Значення цієї функції у кожній точці дорівнює сумі . Аналогічно на множині можна визначити різницю 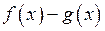, добуток та частку цих функцій (останню крім точок, де .

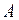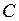Нехай на множині визначено функцію , множиною значень якої є множина . І нехай на множині визначено функцію , множиною значень якої є множина . Припустимо, що . Тоді на деякій підмножині 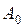множини 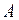визначено так звану складну функцію , множиною значень якої є деяка підмножина 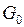множини . Тобто складна функція утворюється шляхом підстановки значень одної функції замість аргумента іншої. 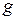така операція називається операцією суперпозиції функцій і .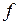

Щоб знайти 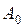– область визначення складної функції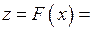 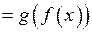, треба з’ясувати, для яких значень значення функції належать області визначення функції . Взагалі кажучи, це досить складна задача. Для її розв’язання, як правило, треба розв’язувати нерівності та системи нерівностей. Значна частина таких нерівностей розглядається у шкільному курсі алгебри.

Розглянемо приклад. Нехай задано функцію .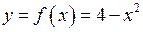

Тут .

І функцію . Тут .

Тоді .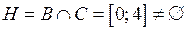

Утворимо за допомогою суперпозиції функцій і складну функцію:

.

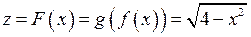Знайдемо її область визначення 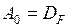. Оскільки , то повинна виконуватись нерівність , звідки 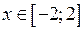. Тобто 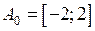. Множина значень складної функції: .

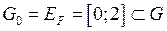Означення. Елементарною функцією називається така функція, яка утворюється з основних елементарних функцій за допомогою скінченого числа операцій додавання, віднімання, множення і ділення, а також операції суперпозиції.

Зауважимо, що тут термін «елементарна» не означає проста. Неелементарні функції можуть бути набагато простішими, ніж елементарні. Наприклад функція

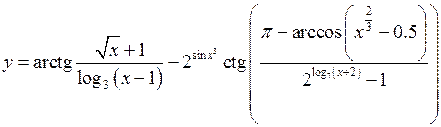являється елементарною (всі потрібні умови виконані). А функція

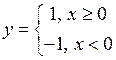елементарною не являється (вона задається різними виразами на різних інтервалах, а цього не передбачено в означенні елементарної функції). Неелементарними являються також, наприклад, функції 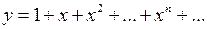(нескінченна кількість арифметичних дій), 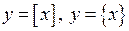(відповідно ціла і дробова частина 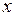), розглянута вище функція Діріхле та ін. До неелементарних відносяться також так звані спеціальні функції, які відіграють дуже важливу роль у природознавстві.

Елементарні функції розділяються на наступні основні класи.

1. Многочлени (або поліноми). Многочленом (поліномом) степеня називається функція виду:

.

Дійсні числа називаються коефіцієнтами многочлена. Зокрема, якщо , то 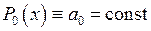. Якщо , то – лінійна функція. Якщо , то – квадратний тричлен.

2. Раціональні функції. Це функції, які є відношенням двох многочленів (не обов’язково однакового степеня):

.

Наприклад:

.

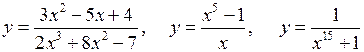Зокрема, многочлени являються частинним випадком раціональних функцій ().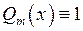

3. Ірраціональні функції Це функції, які утворюються за допомогою скінченого числа арифметичних дій та операцій суперпозиції з раціональних функцій та степеневих з раціональними показниками. Наприклад:

.

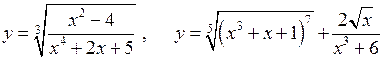Раціональні та ірраціональні функції називаються алгебраїчними. Графіки цих функцій відповідно називаються алгебраїчними кривими. До них, зокрема, відносяться вже відомі вам еліпс, гіпербола і парабола (див. «Аналітична геометрія на площині»).

4. Трансцендентні функції. До цих функцій відносяться ті елементарні функції, які не являються алгебраїчними. Це, зокрема, всі тригонометричні та обернені тригонометричні функції, а також показникові та логарифмічні.

Виділимо деякі важливі типи функцій (вони стосуються не лише елементарних функцій), з якими у подальшому нам доведеться мати справу.

1. Обмежені функції.

Означення. Функція називається обмеженою на множині , якщо таке, що .

Іншими словами значення обмеженої функції не виходять за межі відрізку . З геометричної точки зору це означає, що її графік цілком лежить між прямими 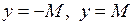(рис. 27).

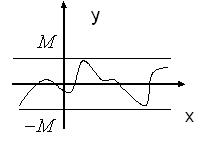
Рис. 27

Одна й та ж функція на одній множині може бути обмеженою, а на іншій ні. Наприклад, функція обмежена на відрізку (на ньому ) і взагалі на будь якому відрізку числової прямої, але не обмежена на всій числовій прямій. Функція 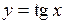обмежена на відрізку (тут 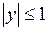), але не обмежена на півінтервалі . Функція обмежена на всій числовій прямій ().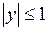

2. Монотонні функції.

Означення. Функція називається зростаючою (спадною) на множині , якщо таких, що 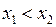, виконана нерівність .

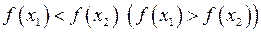Тобто для зростаючої функції більшому значенню аргумента відповідає і більше значення функції, а для спадної більшому значенню аргумента відповідає менше значення функції.

Означення. Функція називається неспадною (незростаючою) на множині , якщо таких, що 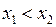, виконано .

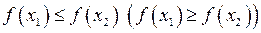Тобто для неспадної функції більшому значенню аргумента відповідає не менше значення функції, а для незротсаючої більшому значенню аогумента відповідає не більше значення функції.

Схематичні графіки цих функцій зображені на рис. 28 (а – зростаюча, б – спадна, в – неспадна, г – незростаюча).

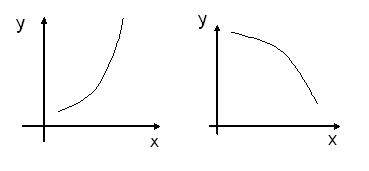
Рис. 28 (а) Рис. 28 (б)

Рис. 28 (в) Рис. 28 (г)

Одна й та ж функція на одних ділянках числової прямої може бути зростаючою, а на інших спадною. Наприклад, функція спадна на 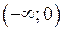і зростаюча на .

Зростаючі, спадні, неспадні та незростаючі функції поєднуються терміном монотонні функції.

3. Парні та непарні функції.

Означення. Функція називається парною (непарною), якщо .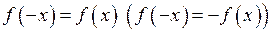

З означення випливає, що область визначення парної чи непарної функції обов’язково симетрична відносно точки . Графік парної функції симетричний відносно осі 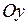(рис. 29 (а)), а непарної – відносно початку координат (рис. 29 (б)).

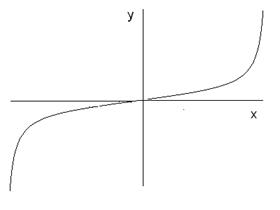
Рис. 29 (а) Рис. 29 (б)

З основних елементарних функцій парними є, наприклад, , , 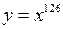, а непарними , , , .

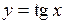Не слід думати, що, якщо функція не є парною, то вона непарна. Існує скільки завгодно функцій, які не являються ні парними, ні непарними. Наприклад 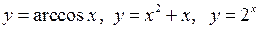тощо.

Для побудови графіка парної чи непарної функції достатньо побудувати її графік тільки у правій півплощині, а потім відобразити симетрично відносно осі (для парної функції), або відносно початку координат (для непарної функції).

4. Періодичні функції.

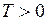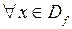Означення. Функція називається періодичною, якщо існує таке , що виконано: .

Число 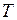називається періодом функції. Очевидно, що періодом буде також будь яке число виду 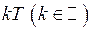. Найменший з додатних періодів називається основним періодом функції.

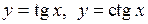З основних елементарних функцій періодичними являються тригонометричні функції. Основний період функцій дорівнює , а функцій дорівнює .

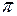Для побудови графіка функції, періодичної з періодом 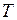достатньо побудувати його на будь якому проміжку довжини 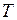(наприклад 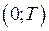), а потім продовжити графік на всю вісь, повторюючи його на кожному проміжку довжини 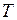. Якщо, крім того, функція парна, чи непарна, то достатньо побудувати її графік на інтервалі .

Лекція 6. Границя функції у точці та у нескінченності.

Дата добавления: 2015-05-24