
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обчислення границь функцій
Розглянемо дві функції 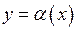 та
та 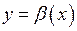 , які є нескінченно малими при
, які є нескінченно малими при 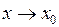 , тобто
, тобто 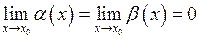 .
.
Означення. Функції 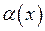 та
та 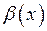 називаються нескінченно малими одного порядку при
називаються нескінченно малими одного порядку при 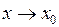 , якщо
, якщо
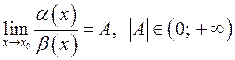 .
.
Тобто границя відношення цих нескінченно малих дорівнює скінченій відмінній від нуля сталій. Тоді пишемо: 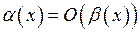 при
при 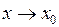 .
.
Якщо, зокрема, 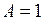 , то нескінченно малі
, то нескінченно малі 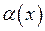 та
та 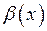 називаються еквівалентними при
називаються еквівалентними при 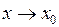 . Тоді пишемо:
. Тоді пишемо: 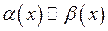 при
при 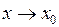 .
.
Приклади.
1. 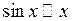 при
при 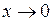 (на підставі першої важливої границі).
(на підставі першої важливої границі).
2. 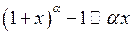 при
при 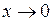 (на підставі першої супутньої границі).
(на підставі першої супутньої границі).
3. 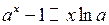 при
при 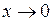 ; зокрема
; зокрема 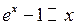 при
при 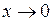 (на підставі
(на підставі
другої супутньої границі).
4.  при
при 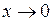 ; зокрема
; зокрема 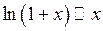 при
при 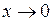
(на підставі третьої супутньої границі).
Означення. Функція 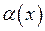 називається нескінченно малою вищого порядку, ніж
називається нескінченно малою вищого порядку, ніж 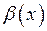 при
при 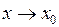 , якщо
, якщо
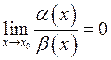 .
.
У цьому випадку пишемо: 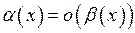 при
при 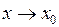 .
.
Наприклад, 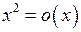 при
при 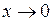 . Взагалі при
. Взагалі при 
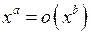 при
при 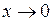 , а
, а 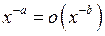 при
при 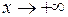 .
.
Покажемо, що 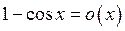 при
при 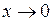 . Дійсно:
. Дійсно:
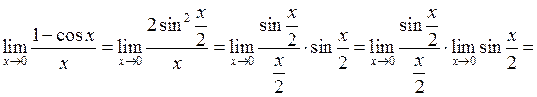
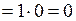 (на підставі першої важливої границі).
(на підставі першої важливої границі).
Використання апарату нескінченно малих дозволяє досить ефективно обчислювати границі функцій. В простіших випадках границю функції у точці можна знайти на підставі теорем про границю суми, різниці, добутку і частки функцій. Відповідний приклад ми розглянули у лекції 7. Вивчення більш складних випадків почнемо з границі відношення двох функцій:
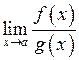 .
.
Якщо існують 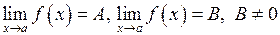 , то границя дорівнює
, то границя дорівнює 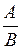 . Але границі як чисельника, так і знаменника можуть дорівнювати нулю, а також можуть бути нескінченними. Нехай, наприклад,
. Але границі як чисельника, так і знаменника можуть дорівнювати нулю, а також можуть бути нескінченними. Нехай, наприклад, 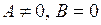 . Тоді границя відношення буде нескінченною, оскільки функція, яка прямує до скінченої відмінної від нуля границі, ділиться на нескінченно малу. Нескінченність вийде і тоді, коли
. Тоді границя відношення буде нескінченною, оскільки функція, яка прямує до скінченої відмінної від нуля границі, ділиться на нескінченно малу. Нескінченність вийде і тоді, коли 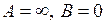 . Якщо
. Якщо 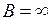 ,
, 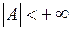 , то границя відношення, очевидно, буде дорівнювати нулю.
, то границя відношення, очевидно, буде дорівнювати нулю.
Підведемо підсумок у вигляді наступної таблиці:

В ній проставлено значення 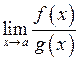 в залежності від
в залежності від  та
та 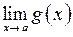 . Ми бачимо, що це значення можна однозначно визначити в усіх випадках, крім двох: а саме, коли границі обох функцій водночас дорівнюють нулю, або водночас дорівнюють нескінченності. Такі ситуації називаються невизначеностями. В даному випадку ми маємо справу з невизначеностями типу
. Ми бачимо, що це значення можна однозначно визначити в усіх випадках, крім двох: а саме, коли границі обох функцій водночас дорівнюють нулю, або водночас дорівнюють нескінченності. Такі ситуації називаються невизначеностями. В даному випадку ми маємо справу з невизначеностями типу 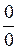 та
та 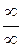 . Границя виразів такого роду може бути і нулем, і скінченим, відмінним від нуля числом, і нескінченністю, і навіть взагалі може не існувати. Якщо вдається встановити, яка саме з цих ситуацій має місце, то кажуть, що невизначеність розкрита.
. Границя виразів такого роду може бути і нулем, і скінченим, відмінним від нуля числом, і нескінченністю, і навіть взагалі може не існувати. Якщо вдається встановити, яка саме з цих ситуацій має місце, то кажуть, що невизначеність розкрита.
Бувають невизначеності інших типів. Найбільш часто зустрічаються наступні.
1. 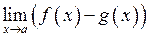 , коли
, коли 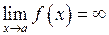 ,
, 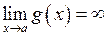 . Це невизначеність типу
. Це невизначеність типу 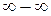 .
.
2. 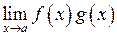 , коли
, коли 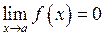 ,
, 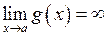 . Це невизначеність типу
. Це невизначеність типу 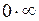 .
.
3. 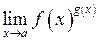 , коли
, коли 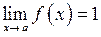 ,
, 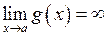 . Це невизначеність типу
. Це невизначеність типу 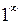 .
.
4. 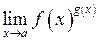 , коли
, коли 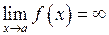 ,
, 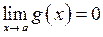 . Це невизначеність типу
. Це невизначеність типу 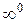 .
.
5. 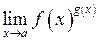 , коли
, коли 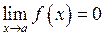 ,
, 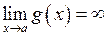 . Це невизначеність типу
. Це невизначеність типу 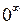 .
.
6. 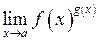 , коли
, коли 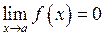 ,
, 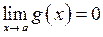 . Це невизначеність типу
. Це невизначеність типу 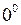 .
.
В багатьох випадках ці невизначеності можна звести до невизначеностей типу 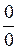 та
та 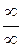 . Тому саме з них ми й почнемо вивчення методів розкриття невизначеностей.
. Тому саме з них ми й почнемо вивчення методів розкриття невизначеностей.
I. Невизначеність типу 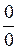 в раціональних виразах.
в раціональних виразах.
Розглянемо границю вигляду:
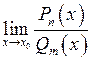 , де
, де 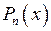 – поліном степеня
– поліном степеня 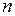 , а
, а 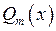 – поліном степеня
– поліном степеня 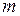 , причому
, причому 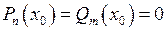 , тобто
, тобто  є коренем обох поліномів. Тоді мають місце співвідношення:
є коренем обох поліномів. Тоді мають місце співвідношення:
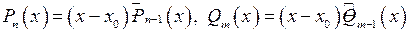 , де
, де 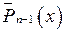 – поліном степеня
– поліном степеня 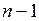 , а
, а 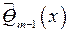 – поліном степеня
– поліном степеня 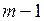 . Підставляючи ці вирази до функції, що стоїть під знаком границі, і, скорочуючи на
. Підставляючи ці вирази до функції, що стоїть під знаком границі, і, скорочуючи на 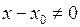 , отримаємо:
, отримаємо:
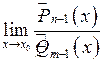 .
.
Якщо хоча б один з поліномів 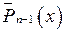 ,
, 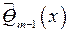 у точці
у точці  не дорівнює нулю, то тоді невизначеність зникає, і ми можемо скористатися вищенаведеною таблицею. Якщо
не дорівнює нулю, то тоді невизначеність зникає, і ми можемо скористатися вищенаведеною таблицею. Якщо 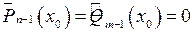 , то треба ще раз повторити описаний прийом.
, то треба ще раз повторити описаний прийом.
Перейдемо до прикладів.
а) 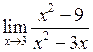 .
.
Тут чисельник і знаменник при 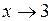 прямують до нуля, отже маємо невизначеність типу
прямують до нуля, отже маємо невизначеність типу 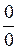 . А тоді:
. А тоді:
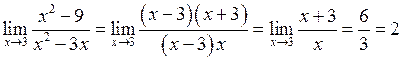 .
.
б) 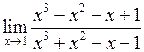 .
.
Тут також має місце невизначеність типу 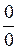 . Розкладемо чисельник і знаменник на множники. Це розкладання можна здійснювати діленням чисельника і знаменника в стовпчик на
. Розкладемо чисельник і знаменник на множники. Це розкладання можна здійснювати діленням чисельника і знаменника в стовпчик на 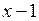 (зокрема, за схемою Горнера), або групуванням доданків у чисельнику і знаменнику.
(зокрема, за схемою Горнера), або групуванням доданків у чисельнику і знаменнику.
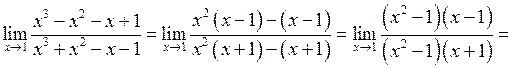
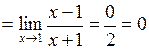 .
.
в) 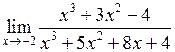 .
.
Очевидно, що при  чисельник і знаменник прямують до нуля, отже маємо невизначеність типу
чисельник і знаменник прямують до нуля, отже маємо невизначеність типу 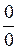 . Розкладемо чисельник і знаменник на множники:
. Розкладемо чисельник і знаменник на множники:
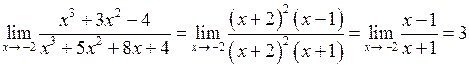 .
.
II. Невизначеність типу 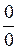 в ірраціональних виразах.
в ірраціональних виразах.
У таких ситуаціях намагаються тим чи іншим чином позбутися ірраціональностей у чисельнику чи у знаменнику.
а) 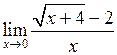 .
.
Помножимо чисельник і знаменник на 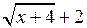 .
.
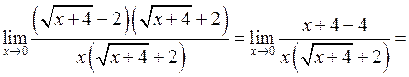
 .
.
б) 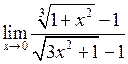 .
.
Помножимо чисельник і знаменник на добуток 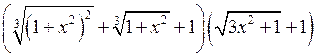 . Отримаємо:
. Отримаємо:
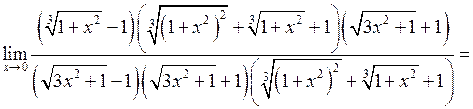
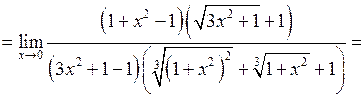
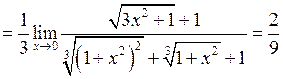 .
.
Іноді від ірраціональності можна позбавитись введенням нової змінної.
в) 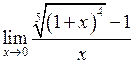 .
.
Введемо заміну 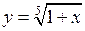 . Тоді
. Тоді 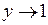 при
при 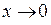 . Маємо:
. Маємо:
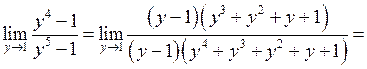
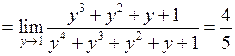 .
.
III. Невизначеність типу 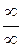 в раціональних виразах.
в раціональних виразах.
У таких ситуаціях ділять чисельник і знаменник на 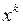 , де
, де 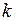 – найвища степінь змінної
– найвища степінь змінної 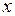 з тих, в яких вона міститься у чисельнику та у знаменнику.
з тих, в яких вона міститься у чисельнику та у знаменнику.
а) 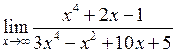 .
.
Маємо невизначеність типу 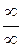 . Найвища степінь
. Найвища степінь 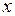 – четверта. Отже поділимо чисельник і знаменник на
– четверта. Отже поділимо чисельник і знаменник на 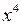 .
.
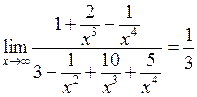 , оскільки вирази вигляду
, оскільки вирази вигляду 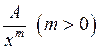 прямують до нуля при
прямують до нуля при 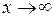 .
.
Застосовуючи цей метод, легко отримати наступний результат. Якщо
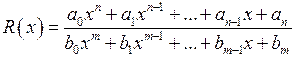 , то
, то
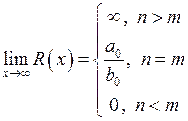
IY. Невизначеність типу 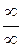 в ірраціональних виразах.
в ірраціональних виразах.
Тут можна також застосовувати метод ділення на 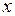 у найвищій степені з тих, в яких він міститься у даному виразі, тільки цього разу ця степінь може бути дробовою.
у найвищій степені з тих, в яких він міститься у даному виразі, тільки цього разу ця степінь може бути дробовою.
а) 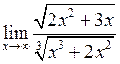 .
.
Поділимо чисельник і знаменник на 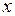 . Тоді вираз під квадратним коренем поділиться на
. Тоді вираз під квадратним коренем поділиться на 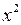 , а під кубічним – на
, а під кубічним – на  . Отримаємо:
. Отримаємо:
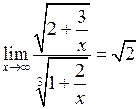 .
.
б) 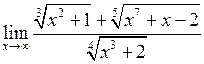 .
.
Тут найвища степінь змінної 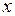 дорівнює
дорівнює 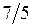 . Отже поділимо чисельник і знаменник на
. Отже поділимо чисельник і знаменник на 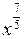 .
.
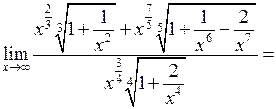
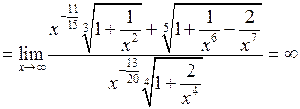 , оскільки вираз у чисельнику прямує до 1 при
, оскільки вираз у чисельнику прямує до 1 при  , а вираз у знаменнику – до нуля.
, а вираз у знаменнику – до нуля.
Y. Невизначеність типу  .
.
Такого типу невизначеності одночасним множенням і діленням на деякий вираз намагаються звести до невизначеностей типу  або
або 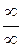 . Розглянемо приклад.
. Розглянемо приклад.
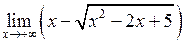 .
.
Помножимо і поділимо на 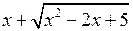 . Отримаємо:
. Отримаємо:
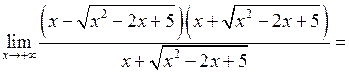
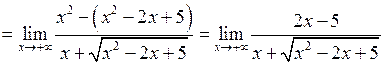 .
.
Отримали невизначеність 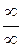 . Ділимо чисельник і знаменник на
. Ділимо чисельник і знаменник на 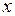 .
.
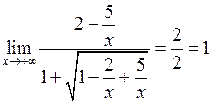 .
.
YI. Використання еквівалентних нескінченно малих.
Нехай треба обчислити
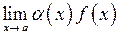 , і нехай функція
, і нехай функція 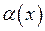 є нескінченно малою при
є нескінченно малою при 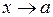 . Припустимо, що при
. Припустимо, що при 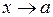 :
: 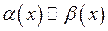 . Тоді
. Тоді
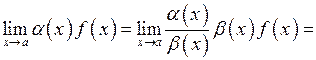
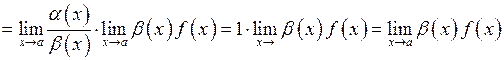 .
.
Аналогічно:
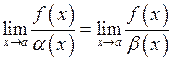 .
.
Таким чином, якщо нескінченно мала міститься під знаком границі у якості множника, або дільника, то її можна замінити на їй еквівалентну.
Зауваження. Суттєво, що нескінченно мала повинна міститись у якості множника або дільника. Якщо вона міститься у якості доданку, то, взагалі кажучи, її не можна замінити на еквівалентну. Наприклад, було б помилкою наступне міркування:
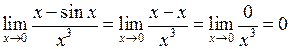 (на підставі того, що
(на підставі того, що 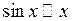 при
при 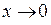 ).
).
Перейдемо до прикладів.
а) 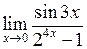 .
.
Невизначеність типу 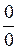 . Замінимо нескінченно малі на їм еквівалентні:
. Замінимо нескінченно малі на їм еквівалентні: 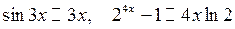 . Отримаємо:
. Отримаємо:
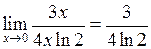 .
.
б) 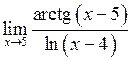 .
.
Невизначеність 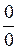 . Зробимо заміну змінної
. Зробимо заміну змінної 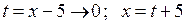 . Тоді отримаємо:
. Тоді отримаємо:
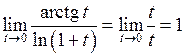 .
.
Тут замінили: 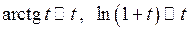 .
.
в) 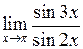 .
.
Невизначеність типу 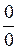 . Але тут була б помилкою заміна
. Але тут була б помилкою заміна 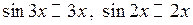 , оскільки тут
, оскільки тут 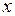 прямує не до нуля, а до відмінної від нуля сталої
прямує не до нуля, а до відмінної від нуля сталої 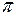 . Тому зробимо заміну змінної:
. Тому зробимо заміну змінної: 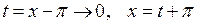 :
:
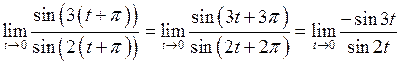 .
.
А тут вже можна замінити 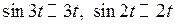 , оскільки
, оскільки 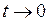 . Тоді
. Тоді
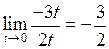 .
.
Використовуючи першу важливу границю, знайдемо площу круга радіуса 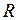 як границю площ вписаних правильних многокутників, які розбито на рівні трикутники, тобто розв’яжемо задачу сформульовану у лекції 3 (рис.12). Площа кожного трикутника дорівнює:
як границю площ вписаних правильних многокутників, які розбито на рівні трикутники, тобто розв’яжемо задачу сформульовану у лекції 3 (рис.12). Площа кожного трикутника дорівнює:
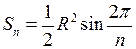 , де
, де 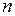 – число сторін многокутника. Тоді площа круга:
– число сторін многокутника. Тоді площа круга:
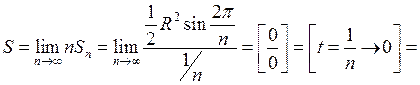
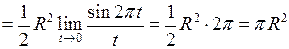 , тобто отримали відому формулу площі круга.
, тобто отримали відому формулу площі круга.
YII. Використання другої важливої границі.
Ця границя використовується для розкриття невизначеностей типу 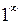 . Здійснюється це наступним чином. Нехай
. Здійснюється це наступним чином. Нехай 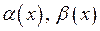 – нескінченно малі при
– нескінченно малі при 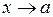 . Розглянемо границю:
. Розглянемо границю:
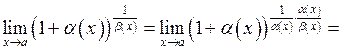
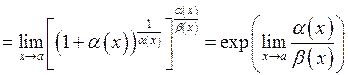 .
.
І тепер все залежить від границі 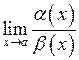 .
.
Перейдемо до прикладів.
а) 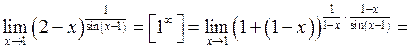
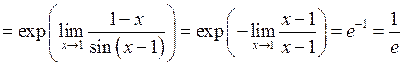 .
.
б) 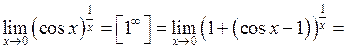
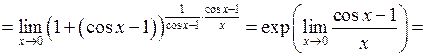
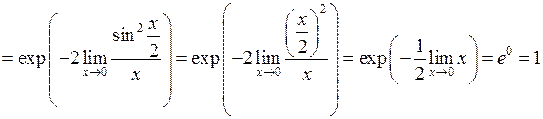 .
.
Лекція 9. Функції, неперервні у точці, та їх властивості.
Розглянемо графіки декількох функцій.
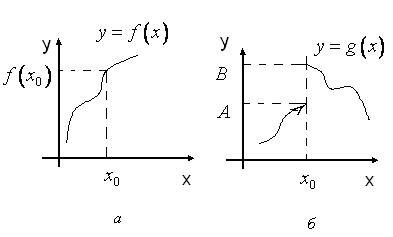
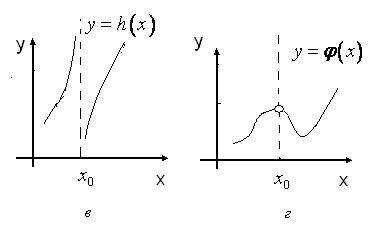
Рис. 33
Яка ознака поєднує графіки, зображені на рис. 33 (б,в,г), на відміну від графіка, зображеного на рис. 33(а)? Ми можемо сказати, що графік на рис. 33(а) є суцільною лінією, в той час, як графіки на рис. 33 (б,в,г) суцільними лініями не являються. Іншими словами, графік на рис. 33(а) можна провести, не видриваючи олівця від паперу, а з графіками рис. 33(б,в,г) це зробити неможливо.
Якщо розглянути точку  на цих графіках, то помітимо, що функція
на цих графіках, то помітимо, що функція 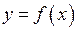 визначена у цій точці, і, якщо змінити значення
визначена у цій точці, і, якщо змінити значення  на малу величину, то значення функції теж зміниться на малу величину. З іншими функціями на рис. 33 така ситуація не спостерігається. Функція
на малу величину, то значення функції теж зміниться на малу величину. З іншими функціями на рис. 33 така ситуація не спостерігається. Функція  змінюється стрибкообразно при переході через точку
змінюється стрибкообразно при переході через точку  . Значення функції
. Значення функції 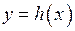 прямують до нескінченності при
прямують до нескінченності при 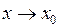 . А функція
. А функція  не визначена у точці
не визначена у точці  , хоча має у цій точці скінчені однобічні границі.
, хоча має у цій точці скінчені однобічні границі.
Такі властивості функцій відображають відповідні властивості процесів, які цими функціями описуються. Розглянемо приклади.
1. Залежність атмосферного тиску 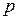 від висоти над рівнем моря
від висоти над рівнем моря 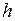 задається барометричною формулою (див. розділ «Диференціальні рівняння»):
задається барометричною формулою (див. розділ «Диференціальні рівняння»):
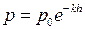 , де
, де 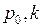 – додатні сталі. Графік цієї функції має вид
– додатні сталі. Графік цієї функції має вид
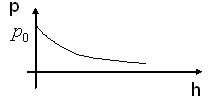
Рис. 34
Бачимо, що це суцільна лінія, тобто графік типу 33(а).
2. Відомо, що залежність електричного опору металів 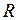 від температури
від температури 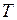 має приблизно лінійний характер, коли
має приблизно лінійний характер, коли 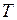 вище деякої критичної точки
вище деякої критичної точки 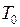 (своєї для кожного металу). Якщо
(своєї для кожного металу). Якщо 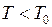 , то опір
, то опір 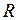 різко падає майже до нуля. Це явище називається надпровідністю. Спостерігається воно при дуже низьких температурах, близьких до абсолютного нуля. Наприклад для алюмінія ця температура дорівнює
різко падає майже до нуля. Це явище називається надпровідністю. Спостерігається воно при дуже низьких температурах, близьких до абсолютного нуля. Наприклад для алюмінія ця температура дорівнює 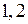 градуса за шкалою Кельвіна. Близьке до нього явище надтікучесті, коли деякі рідини при досягненні певної критичної температури (теж дуже низької; наприклад, для рідкого гелія вона складає 2,19 градусів за шкалою Кельвіна) майже повністю втрачають в’язкість.
градуса за шкалою Кельвіна. Близьке до нього явище надтікучесті, коли деякі рідини при досягненні певної критичної температури (теж дуже низької; наприклад, для рідкого гелія вона складає 2,19 градусів за шкалою Кельвіна) майже повністю втрачають в’язкість.
Схематична залежність електричного опору металів від температури показана на рис. 35.
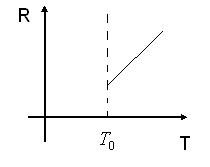
Рис. 35
3. Залежність густини ідеального газу від температури 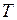 виражається формулою:
виражається формулою:
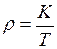 , де
, де 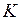 – стала. Графік такої залежності має вид:
– стала. Графік такої залежності має вид:
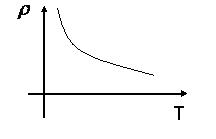
Рис. 36
Тобто маємо графік типу 33(в). Існують також процеси типу 33(г). Все це свідчить про те, що ми повинні вміти встановлювати подібні властивості функцій і не лише у тих випадках, коли є графічні їх зображення, а й тоді, коли функції задаються аналітичним способом. Але це можливо тільки тоді, коли ми маємо чіткі математичні означення всіх цих ситуацій. Отже саме до них ми тепер і переходимо.
Означення. Функція 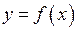 називається неперервною у точці
називається неперервною у точці  , якщо виконані наступні умови:
, якщо виконані наступні умови:
1) функція визначена у точці  , тобто існує значення
, тобто існує значення  ,
,
2) існує 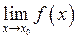 ,
,
3) 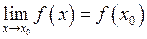 .
.
Якщо використати означення границі функції у точці на мові «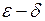 », то можна означення неперервності функції у точці сформулювати так:
», то можна означення неперервності функції у точці сформулювати так:
Функція 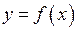 називається неперервною у точці
називається неперервною у точці  , якщо вона визначена у точці
, якщо вона визначена у точці  , і
, і 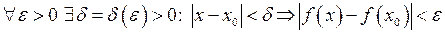 .
.
Зверніть увагу: у означенні границі функції у точці суттєвою особливістю, як ми відмічали, була умова, що 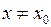 , або
, або 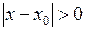 . Тобто функція могла бути невизначеною в точці
. Тобто функція могла бути невизначеною в точці  . І навіть у тому випадку, коли вона визначена у цій точці, границя функції зовсім не обов’язково дорівнює значенню
. І навіть у тому випадку, коли вона визначена у цій точці, границя функції зовсім не обов’язково дорівнює значенню  . У випадку неперервності ці особливості зникають. Функція визначена у точці
. У випадку неперервності ці особливості зникають. Функція визначена у точці  , і границя функції при
, і границя функції при 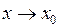 дорівнює значенню функції в точці
дорівнює значенню функції в точці  .
.
Враховуючи, що 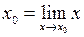 , можна третю умову неперервності записати так:
, можна третю умову неперервності записати так:
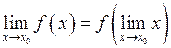 .
.
Тобто знаки границі і неперервної функції можна змінювати місцями.
Можна дати інше означення неперервності функції у точці. Позначимо через 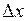 різницю
різницю 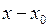 і назвемо цю величину приростом аргумента у точці
і назвемо цю величину приростом аргумента у точці  . Якщо
. Якщо 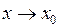 , то
, то 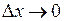 і навпаки. Різниця відповідних значень функції
і навпаки. Різниця відповідних значень функції 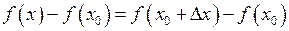 називається приростом функції у точці
називається приростом функції у точці  і позначається
і позначається 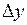 (рис. 37).
(рис. 37).
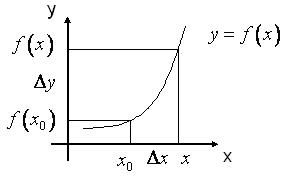
Рис. 37
Тепер, оскільки 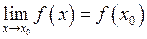 , то
, то 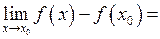
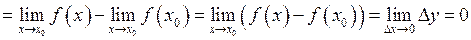 .
.
Таким чином, функція називається неперервною у точці  , якщо нескінченно малому приросту аргумента у цій точці відповідає нескінченно малий приріст функції.
, якщо нескінченно малому приросту аргумента у цій точці відповідає нескінченно малий приріст функції.
Геометрично факт неперервності функції у точці  означає, що в околі точці
означає, що в околі точці  графік функції є суцільною лінією.
графік функції є суцільною лінією.
Приклади.
1. Довести, що функція 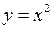 неперервна у будь якій точці числової прямої.
неперервна у будь якій точці числової прямої.
Візьмемо довільне 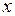 і надамо нескінченно малий приріст
і надамо нескінченно малий приріст 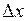 . Тоді функція отримає приріст:
. Тоді функція отримає приріст:
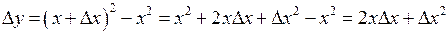 .
.
Величина 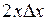 – нескінченно мала при
– нескінченно мала при 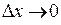 як добуток обмеженої функції
як добуток обмеженої функції 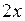 на нескінченно малу
на нескінченно малу 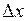 , а
, а 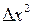 – нескінченно мала як добуток двох нескінченно малих. Отже
– нескінченно мала як добуток двох нескінченно малих. Отже 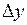 – нескінченно мала як сума двох нескінченно малих, а це й означає неперервність функції
– нескінченно мала як сума двох нескінченно малих, а це й означає неперервність функції 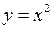 у точці
у точці 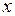 .
.
2. Довести, що функція 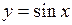 неперервна у будь якій точці числової прямої.
неперервна у будь якій точці числової прямої.
Візьмемо довільне 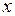 і надамо нескінченно малий приріст
і надамо нескінченно малий приріст 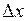 . Тоді функція отримає приріст:
. Тоді функція отримає приріст:

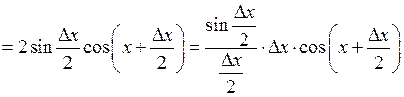 .
.
Функція 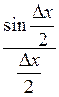 обмежена при
обмежена при  , оскільки вона має скінчену границю при
, оскільки вона має скінчену границю при  (перша важлива границя), функція
(перша важлива границя), функція 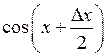 – обмежена, а
– обмежена, а 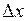 – нескінченно мала, як добуток обмеженої функції на функцію нескінченно малу. Таким чином функція
– нескінченно мала, як добуток обмеженої функції на функцію нескінченно малу. Таким чином функція 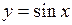 неперервна у кожній точці числової прямої.
неперервна у кожній точці числової прямої.
3. Довести, що функція 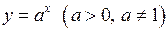 неперервна у кожній точці числової прямої.
неперервна у кожній точці числової прямої.
Знову надаємо довільному 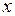 нескінченно малий приріст
нескінченно малий приріст 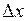 і розглядаємо:
і розглядаємо:
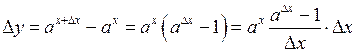 .
.
Функція 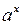 стала відносно
стала відносно 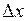 , функція
, функція 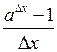 обмежена при
обмежена при 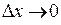 , оскільки має скінчену границю при
, оскільки має скінчену границю при 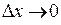 (друга супутня границя), функція
(друга супутня границя), функція 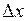 – нескінченно мала, отже
– нескінченно мала, отже 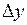 – нескінченно мала, що й означає неперервність функції
– нескінченно мала, що й означає неперервність функції 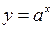 у точці
у точці 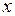 .
.
Аналогічним чином можна довести, що будь яка з основних елементарних функцій неперервна у своїй області визначення.
4. Довести, що функція
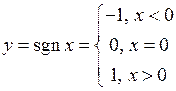 не являється неперервною у точці
не являється неперервною у точці 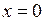 .
.
Надамо значенню аргумента 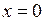 нескінченно малий додатний приріст
нескінченно малий додатний приріст 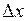 . Тоді функція отримає приріст:
. Тоді функція отримає приріст:
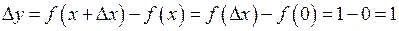 , а ця величина не є нескінченно малою при
, а ця величина не є нескінченно малою при 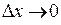 . Отже наша функція не є неперервною у точці
. Отже наша функція не є неперервною у точці 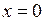 .
.
Функції, неперервні в точці, мають деякі прості властивості, які являються наслідками відповідних властивостей границь функцій.
Теорема. Якщо функції 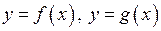 – неперервні у точці
– неперервні у точці  , то функції
, то функції 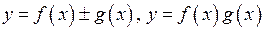 також неперервні у точці
також неперервні у точці  . Якщо додатково
. Якщо додатково 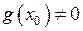 , то функція
, то функція 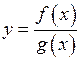 також неперервна у точці
також неперервна у точці  .
.
Доведення. Оскільки 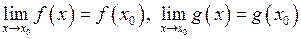 , то на підставі властивостей границь
, то на підставі властивостей границь 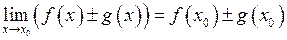 , а також
, а також 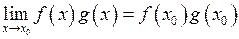 , і, якщо
, і, якщо 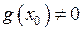 , то
, то 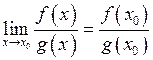 , що й означає неперервність суми, різниці, добутку і частки.
, що й означає неперервність суми, різниці, добутку і частки.
Теорема. Нехай функція 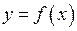 неперервна у точці
неперервна у точці 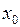 , а функція
, а функція 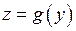 неперервна у точці
неперервна у точці  . Тоді складена функція
. Тоді складена функція 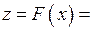
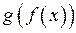 неперервна у точці
неперервна у точці 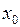 .
.
Доведення. Надамо значенню 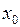 нескінченно малий приріст
нескінченно малий приріст 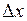 . Тоді функція
. Тоді функція 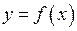 отримає приріст
отримає приріст 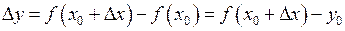 , який також нескінченно малий внаслідок неперервності функції
, який також нескінченно малий внаслідок неперервності функції 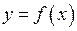 . Функція
. Функція 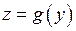 у свою чергу отримає приріст
у свою чергу отримає приріст 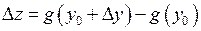 , який також нескінченно малий внаслідок неперервності функції
, який також нескінченно малий внаслідок неперервності функції 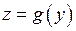 . Отже нескінченно малому приросту аргумента
. Отже нескінченно малому приросту аргумента 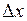 відповідає нескінченно малий приріст
відповідає нескінченно малий приріст 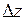 функції
функції 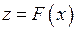 , а це й означає неперервність цієї функції у точці
, а це й означає неперервність цієї функції у точці 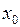 .
.
З цих двох теорем і з того, що основні елементарні функції неперервні в усіх точках їх області визначення, випливає таке твердження.
Теорема. Всі елементаорні функції неперервні в усіх точках їх області визначення.
Лекція 10. Функції, неперервні на відрізку, та їх
|
|
Дата добавления: 2015-05-24; Просмотров: 2681; Нарушение авторских прав?; Мы поможем в написании вашей работы!