Друга важлива границя

.

Перша важлива границя.

Доведемо це співвідношення спочатку для 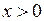. Виконаємо наступну геометричну побудову (рис. 31).

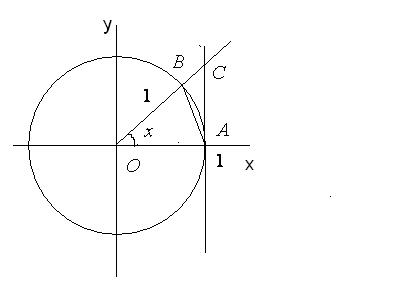
Рис. 31

Побудуємо коло з центром у початку координат і радіусом 1. Проведемо радіус 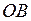цього кола під кутом 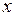(в радіанах) до додатного напряму осі абсцис, причому продовжимо його за коло.

Через точку 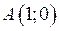проведемо пряму, перпендикулярну осі абсцис (дотичну до кола). Точку перетину цієї прямої і продовження радіусу 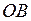позначимо через .

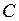Тоді площа трикутника 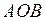буде дорівнювати 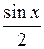, площа сектора 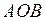дорівнює 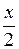, а площа трикутника 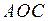дорівнює 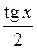. Очевидна подвійна нерівність:

.

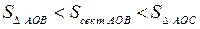Або:

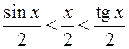, тобто

.

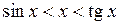Оскільки тут 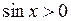, то поділивши на 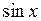, матимемо:

.

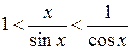Або:

.

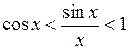Якщо тепер 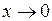, то 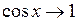, і на підставі теореми про проміжну функцію буде: 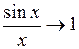, тобто потрібна рівність доведена.

У випадку, коли 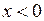введемо 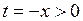, і тоді:

.

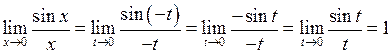Таким чином перша важлива границя повністю доведена.

Визначимо деякі наслідки з першої важливої границі.

1. .

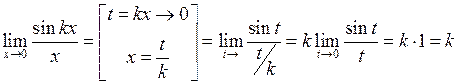2. .

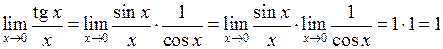3. .

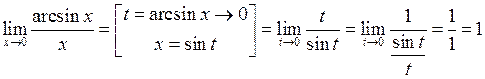4. 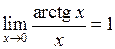(аналогічно попередньому).

Можна довести, що функція 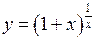при 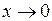має скінчену границю. Ця границя у математиці позначається буквою 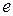, тобто

.

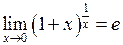Це співвідношення називають другою важливою границею, а число 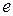називають числом Ейлера*. Число це ірраціональне, отже його можна зобразити нескінченним неперіодичним десятковим дробом. Більше того, Ш.Ермітом** було встановлено, що 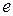– число трансцендентне, тобто воно не являється коренем ніякого алгебраїчного рівняння з цілими коефіцієнтами (як і число 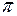). Точно його, очевидно, не можна обчислити, а наближене з точністю до 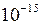значення дорівнює 2,718281828459045. Ця вражаюча низка цифр дуже легко запам’ятовується. 2,7 запам’ятовується само собою, а далі двічі повторюється одна й та ж група цифр: 1828. Це рік народження видатного російського письменника Л.М.Толстого, а також рік народження відомого французького письменника Жюля Верна, мабуть завдяки творам якого, значна кількість читаючих молодих людей обирають спеціальність «географія». Після цього йде також легка група цифр: 45 90 45. Для переважної більшості задач, які ми будемо розглядати, достатньо наближеної рівності: .

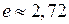Показникова функція за основою 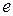, тобто 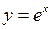(пишуть також 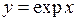) називається експонентою. Це одна з найважливіших для математики і природознавства (зокрема, географії) функцій. За експоненціальним законом відбувається, наприклад, зміна атмосферного тиску залежно від висоти над рівнем моря, розпад радіоактивних речовин (див. розділ курсу «Диференціальні рівняння»), процеси розмноження живих організмів та багато інших.

Логарифми за основою 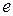називаються натуральними логарифмами і позначаються 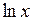. Для задач вищої математики найзручніше використання саме цих логарифмів; внаслідок цього низка формул значно спрощується.

Від логарифма за довільною основою 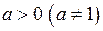можна перейти до натуральних за формулою:

.

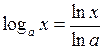Зокрема, для десяткових логарифмів ():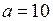

.

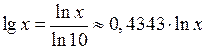Крім першої та другої важливих границь часто зустрічаються наступні границі, які називаються супутними (ми їх наводимо без доведення).

1. 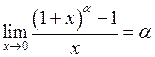, зокрема .

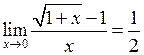2. 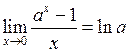, зокрема .

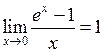3. 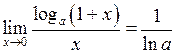, зокрема .

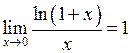В заключній частині лекції ми розглянемо поняття однобічних границь функцій.

Означення. Число 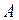називається границею зліва функції 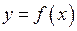при 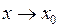, якщо .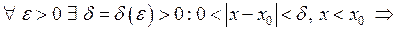

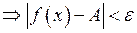У цьому випадку пишемо: .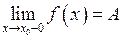

Означення. Число 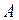називається границею справа функції 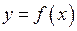при 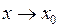, якщо .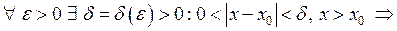

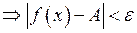У цьому випадку пишемо: .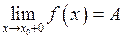

Тобто у першому означенні 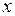прямує до 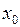, залишаючись весь час меншим, ніж 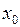, а у другому означенні – залишаючись весь час більшим, ніж 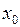. Границі справа і зліва функції 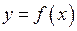у точці 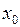називаються однобічними границями функції у цій точці.

Розглянемо приклади.

1.

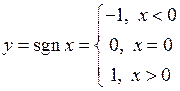
Покажемо, що 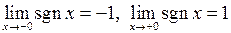. Спочатку розглянемо випадок . Задамо довільне і за цим 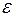знайдемо 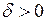таке, що з нерівності 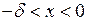буде випливати нерівність 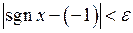. Дійсно, якщ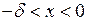о , то 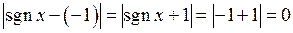, тобто у якості 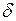можна взяти будь яке додатне число. Таким чином 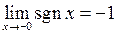. Аналогічно показуємо, що .

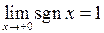2. Покажемо, що 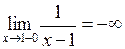, а .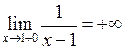

Нехай спочатку 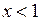. Задамо довільне 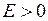і покажемо, що існує таке 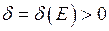, що з нерівності 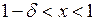буде випливати 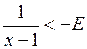. Дійсно, оскільки 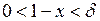, то 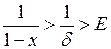, якщо тільки 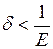. А звідси випливає, що 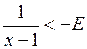, що й треба було встановити. Аналогічно доводиться, що .

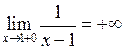Той факт, що 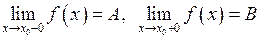, геометрично ілюструється на рис. 32.

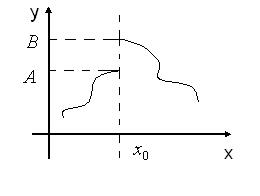
Рис. 32

Теорема. Рівність 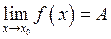має місце тоді і тільки тоді, коли у точці 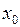існують однобічні границі, і вони дорівнюють .

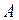Доведення. Нехай спочатку 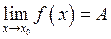. Тоді 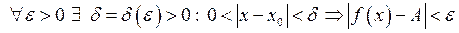. Це означає, що нерівність 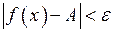справджується як для 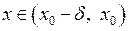, так і для 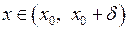. А це згідно означенню однобічних границь означає, що .

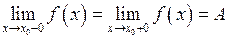Нехай тепер 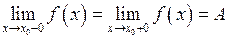. Тоді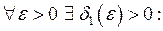 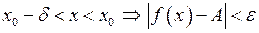. А також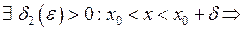 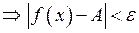. Візьмемо 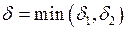. Тоді якщо 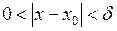, то буде виконана нерівність 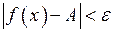, що й означає, що 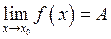. Теорему доведено.

Наступну теорему ми наводимо без доведення.

Теорема. Якщо існує такий інтервал 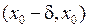, що у цьому інтервалі функція 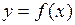є монотонною та обмеженою, то існує скінченна границя 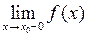. Якщо існує такий інтервал 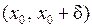, що у цьому інтервалі функція 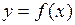є монотонною та обмеженою, то існує скінченна границя .

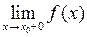Лекція 8. Порівняння нескінченно малих. Деякі методи

Дата добавления: 2015-05-24