Нескінченно великі послідовності, зв'язок з нескінченно малими

Властивості границь.

Нескінченно малі послідовності та їх властивості.

Означення. Послідовність 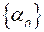називається нескінченно малою, якщо її границя дорівнює нулю.

Властивості нескінченно малих послідовностей:

1. Алгебраїчна сума фіксованого числа нескінченно малих послідовностей є нескінченно мала послідовність.

2. Добуток нескінченно малої послідовності на обмежену послідовність (в тому числі на сталу, іншу нескінченно малу послідовність) є нескінченно мала послідовність.

Властивість 1. Якщо всі члени послідовності дорівнюють 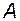, то і границя цієї послідовності дорівнює .

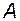Властивість 2. Якщо послідовність 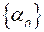має границю 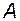, то послідовність – нескінченно мала.

Властивість 3. Якщо послідовність 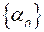має границю, то вона єдина.

Означення. Послідовність називається нескінченно великою, якщо для 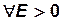знайдеться номер , починаючи з якого правильна нерівність .

Приклад 2.4. Довести, що послідовність , 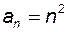нескінченно велика.

Розв’язування. Нехай , тобто 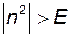. Для 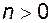виконується нерівність 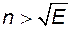. Візьмемо 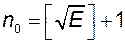. Тоді для правильна нерівність .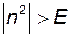

Теорема. Якщо послідовність 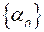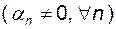– нескінченно мала, то послідовність , – нескінченно велика, і навпаки, якщо послідовність – нескінченно велика, то послідовність – нескінченно мала.

Дата добавления: 2015-05-24