Теоретическая часть. Формирование навыков экспериментального изучения равновесия гомогенной реакции в растворе Fe2(SO4)3 + 2 KJ 2FeSO4 + J2 + K2SO4 при разных температурах

Цель работы

Формирование навыков экспериментального изучения равновесия гомогенной реакции в растворе Fe₂(SO₄)₃ + 2 KJ 2FeSO₄ + J₂ + K₂SO₄ при разных температурах, расчетов константы равновесия и термодинамических функций ΔН, ΔG и ΔS.

Химические реакции делятся на гомогенные и гетерогенные. Гомогенными реакциями называют реакции, протекающие в пределах одной фазы. К гомогенным реакциям относятся многие химические процессы, протекающие в газовой фазе или в растворах. Примерами могут служить реакции:

СО_(г) + Н₂О_(г) СО_2(г) + Н_2(г);

СН₃СООН_(ж) + С₂Н₅ОН_(ж) СН₃СООС₂Н_5(ж) + Н₂О_(ж)

Химическая реакция, протекающая на границе раздела фаз, называется

гетерогенной. Примеры гетерогенных реакций:

СаО_(тв) + СО_2(г) СаСО_3(тв);

С_(тв) + О_2(г) СО_{2 (г)}

Реакция протекает до равновесия, при котором имеются как продукты, так

и реагенты, и при этом не происходит изменение их концентраций. Иногда

количество продукта значительно превышает количество оставшихся

реагентов в равновесной смеси, и с практической точки зрения реакция

завершается. Реакционная смесь при равновесии содержит значительные

концентрации как реагентов, так и продуктов.

Для предсказания равновесных концентраций в любых условиях реакции

применяют термодинамические расчеты. Естественным направлением

химических реакций является направление к минимуму энергии Гиббса.

Величина, количественно характеризующая термодинамическую

возможность протекания данной химической реакции, равная - 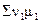, т.е.

алгебраической сумме произведений химических потенциалов μ₁ всех

веществ, участвующих в реакции, на их стехиометрические коэффициенты ν₁

в уравнении реакции с обратным знаком, называется химическим сродством.

Допустим, что протекает реакция по уравнению А В при постоянной

температуре и давлении. Элементарное изменение энергии Гиббса можно

записать в виде:

dG = μ_Adn_A + μ_Bdn_B (p,T = const).

где μ – химические потенциалы реагентов и продуктов реакций;

dn₁ – изменение молярных количеств реагентов и продуктов реакций.

Условием термодинамического химического равновесия является соотношение

концентраций продуктов реакции и исходных веществ, при котором в

реакционной системе dG = 0 (∑μ₁dn₁ = 0), причем энергия Гиббса имеет

минимальное значение.

Молекулярно-статистически химическое равновесие определяется как состояние,

при котором скорости прямой и обратной реакций равны друг другу, при этом

равновесие наступает тогда, когда состав смеси с течением времени при

постоянных внешних условиях не меняется, Однако, неизменяемость состава

смеси с течением времени может служить признаком достаточным для

констатирования наступившего равновесия лишь в том случае, если эта

неизменяемость была достигнута в итоге самой реакции, т.е. при условии, что

состав смеси до некоторого времени менялся вследствии реакции, а потом

перестал меняться.

Иногда состав смеси, в которой возможна химическая реакция, остается

продолжительно неизменным, но не потому, что процесс уже закончился и

наступило равновесие, а вследствие того, что без катализатора процесс протекает

настолько медленно, что происходящие изменения не могут быть

экспериментально обнаружены. Для установления равновесия можно

воспользоваться вторым признаком равновесия – признаком его подвижности.

Система, находящаяся в равновесии, может быть выведена из этого положения

внешним воздействием. При прекращении воздействия система самопроизвольно

возвращается в прежнее состояние. При изменении внешних условий (

температуры, давления и т.п.) состав смеси будет изменяться. При возвращении

системы к первоначальным условиям она будет переходить к исходному

состоянию. Это означает, что рассматриваемое состояние является равновесным.

Если же этого нет, то система не достигла еще состояние равновесия.

Система, состояние которой характеризуется двумя признаками –

неизменяемостью состава и подвижностью, - называется равновесной системой, а

состав ее - равновесным составом.

Состояние равновесия химической реакции характеризуется

термодинамической константой равновесия К_а. Величина К_а выражается для

данной химической реакции

v₁B₁ + v₂B₂ + ………………+ v₁B₁ = n₁C₁ + n₂C₂ + ……….. + n₁C₁

соотношение между активностями а₁ участвующих в ней веществ при

равновесии:

Ка =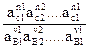

Аналогичное соотношение между молярно- объемными концентрациями

выражает константу равновесия Кс. Когда к реакционной системе применимы

законы идеальных смесей (идеальных газов, идеальных жидких растворов), Кс

при данной температуре имеет постоянное значение, не зависящее от исходных

концентраций реагентов.

Константу равновесия можно выразить через равновесные парциальные

давления системы:

Кр = 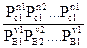(6)

Константу равновесия можно выразить через общее давление системы и

равновесный состав. Например, при проведении реакции

СО + 2Н₂ СН₃ОН

Исходные вещества были взяты в стехиометрическом соотношении: 1 моль СО и 2 моля Н₂. При равновесии получено х моль СН₃ОН. Тогда (1-х) – равновесное количество молей СО; 2(1-х) – равновесное количество молей Н₂. Парциальное давление равно общему давлению, умноженному на молярную долю данного компонента:

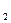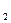Р_СО = Рх_СО; Р_Н = Рх_Н ; Р_{СН 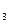ОН} = Рх_{СН 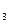ОН} (7)

Где Р = 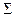Р₁ – общее давление в системе; х₁ – молярная доля 1-го компонента. Для определения молярной доли необходимо рассчитать общее равновесное количество молей в системе:

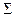n₁, равн = (1-х) + 2(1-х) + х = 3 -2х;

х₁ = n_{1 равн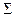} / n_{1 равн.};

х_СО = (1 – х) / (3 – 2х),

х_Н 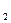= 2(1 – х) / (3 – 2х),

х_{СН 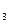ОН} = х / (3 - 2х).

Константа равновесия данной реакции равна:

Кр = 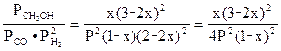. (8)

Равновесие системы может смещаться при изменении начальных концентраций реагирующих веществ, константа же равновесия остается неизменной. Поэтому, зная константу равновесия при каких-либо внешних условиях, начальные концентрации и общее давление, можно рассчитать равновесный выход.

При изучении химической реакции важно знать, будет ли она протекать, а если будет, то в каком направлении. При р,Т = const реакция протекает самопроизвольно в направлении уменьшении энергии Гиббса. Если все реагирующие вещества подчиняются законам идеальных газов, то ее уменьшение, наблюдаемое при обратимом протекании реакции до состояния равновесия выражается уравнением:

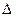- G = RTlnK_p – RT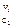[(P 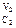P 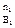) / (P P 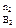) ] (9)

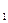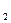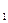где Р_С , Р_С , Р_В , Р_В 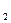- произвольные парциальные давления исходных и конечных веществ. Уравнение (9) позволяет установить влияние температуры, давления инертного газа и начальных концентраций реагентов на направленность химической реакции. В стандартном состоянии при всех парциальных давлениях, равных 1 атм:

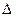- G = RTlnK_p.

Зависимость константы равновесия от температуры описывается уравнением Вант – Гоффа:

.

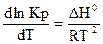Где ΔН⁰ – изменение энтальпии (тепловой эффект) реакции. Знак теплового эффекта определяет знак производной dlnKp/dT. Если ΔН = 0, то константа равновесия не зависит от температуры.

Чтобы вычислить константу равновесия при любой температуре, следует проинтегрировать уравнение Вант-Гоффа. При допущении независимости теплового эффекта от температуры интегрирование уравнения (11) дает приближенное выражение:

ln Kp = - 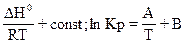(12)

где А = - 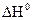/RT, B = const - константа интегрирования.

Или

ln 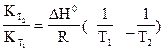(13)

Дата добавления: 2015-05-09