Принципы управления объектами

Лекция №2

Общая структура проектируемой системы, её основные элементы и принцип управления в значительной мере определяются свойствами объекта регулирования, условиями работы системы и требованиями, предъявляемыми к её точности. САУ должна решать две основные задачи:

1. Обеспечить требуемое изменение регулируемых величин;

2. Скомпенсировать действие на объект регулирования возмущений.

Преобразуем обобщённую структурную схему САУ к виду

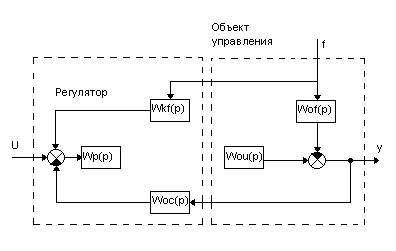
Структурная схема САУ

В общем случае управление регулирующим органом осуществляется в функции ¦, y, x:

.

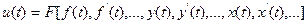Это уравнение преобразуем по Лапласу при нулевых начальных условиях, полагая систему линейной:

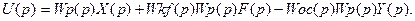(1)

Уравнение объекта регулирования с одной регулируемой функцией при воздействии на него возмущения имеет вид

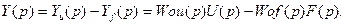(2)

Подставив (1) в (2), получим закон функционирования системы:

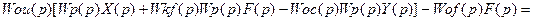
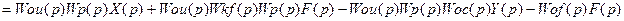
или

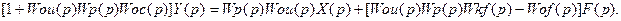
Отсюда

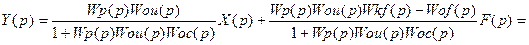
=Wзх(p)X(p)+Wзf(p)F(p), (3)

где Wзх(p) – передаточная функция системы по каналу управления,

Wзf(p) - передаточная функция системы по каналу возмущения.

Для того чтобы регулируемая функция y изменялась по закону x(t) при любых внешних возмущениях, необходимо, чтобы Wзf(p) 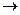0, а Wзx(p) 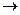1 (если неединичная обратная связь, то Wзx(p) 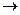1/Kос) при всех условиях работы системы, т.е. необходимо с помощью сил, создаваемых регулирующим органом, скомпенсировать влияние возмущающих воздействий, действующих на объект регулирования, и приложить к объекту такие силы, которые бы обеспечили требуемое изменение регулируемой величины у(t).

Из (3) видно, что эти задачи могут быть решены различными способами, так как при этом необходимо выполнить два условия, а в законе управления (1) имеется три варьируемых оператора: Wp(p), Wkf(p), Wос(p). Один из операторов может быть произвольным.

Дата добавления: 2015-05-09