
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЛЧХ контура с отрицательной обратной связью
|
|
|
|
Пример
Пусть задана передаточная функция объекта
 .
.
Требуется построить асимптотическую ЛАЧХ объекта.
1. Выделение элементарных звеньев.
Вынесем множитель из каждой скобки так, чтобы свободный член в этой скобке был равен 1:
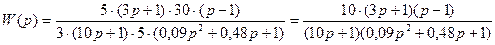 .
.
Корни квадратного трёхчлена в знаменателе комплексно-сопряжённые, поэтому можно представить заданную передаточную функцию в виде произведения передаточного коэффициента и четырёх передаточных функций элементарных звеньев:
 ,
,
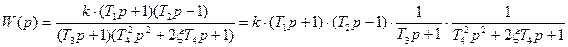 ,
,
где  .
.
Звенья с передаточными функциями  и
и 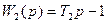 - идеальные звенья с введением производной, второе из них – неминимально - фазовое. Звено с передаточной функцией
- идеальные звенья с введением производной, второе из них – неминимально - фазовое. Звено с передаточной функцией 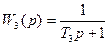 - апериодическое звено, а звено с
- апериодическое звено, а звено с 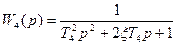 - колебательное, поскольку
- колебательное, поскольку 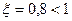 .
.
2. Определение сопрягающих частот.
Сопрягающие частоты – это точки излома ЛАЧХ. Они определяются как 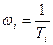 . Таким образом,
. Таким образом,
 рад/с,
рад/с, 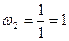 рад/с,
рад/с,
 рад/с,
рад/с, 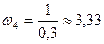 рад/с.
рад/с.
Поскольку при построении ЛАЧХ на оси абсцисс откладывается lgω, вычислим десятичные логарифмы этих частот:
 ,
,  ,
,
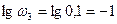 ,
,  .
.
3. Построение ЛАЧХ.
Отметим найденные точки излома ЛАЧХ на оси абсцисс:

Поскольку интегрирующие и дифференцирующие звенья в системе отсутствуют, на низких частотах (примерно до первой сопрягающей частоты  ) система имеет постоянное усиление, равное k=10. Учитывая, что амплитудная характеристика откладывается в логарифмическом масштабе (в децибеллах) получаем
) система имеет постоянное усиление, равное k=10. Учитывая, что амплитудная характеристика откладывается в логарифмическом масштабе (в децибеллах) получаем
20lgk=20lg10=20
и можно сразу нарисовать начальный участок ЛАЧХ:
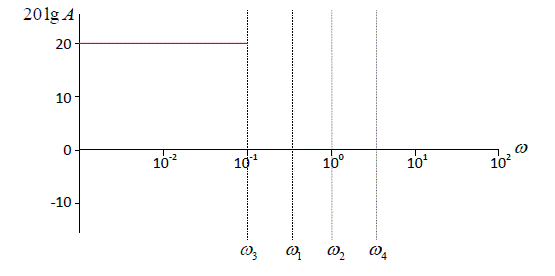
На частоте  вступает в действие апериодическое звено, которое даёт наклон -20 дБ/дек, в интервале от
вступает в действие апериодическое звено, которое даёт наклон -20 дБ/дек, в интервале от  до
до 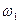 график спускается вниз на
график спускается вниз на

 дБ, поэтому ордината для частоты
дБ, поэтому ордината для частоты 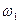 равна
равна  дБ:
дБ:

На частоте 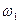 идеальное звено с введением производной добавляет наклон +20 дБ/дек, таким образом, общий наклон становится равен нулю:
идеальное звено с введением производной добавляет наклон +20 дБ/дек, таким образом, общий наклон становится равен нулю:

На частоте  неминимально – фазовое идеальное звено с введением производной ещё добавляет наклон +20 дБ/дек, таким образом, общий наклон становится равен +20 дБ/дек. В интервале от
неминимально – фазовое идеальное звено с введением производной ещё добавляет наклон +20 дБ/дек, таким образом, общий наклон становится равен +20 дБ/дек. В интервале от  до
до 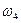 график поднимается на
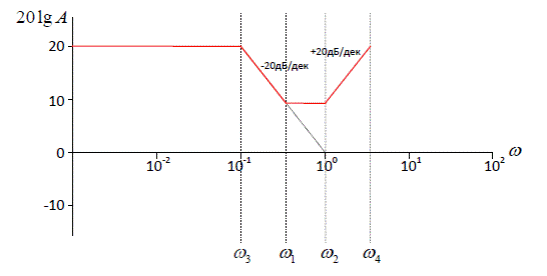
график поднимается на 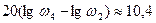 дБ, поэтому ордината для частоты
дБ, поэтому ордината для частоты 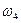 равна 9,6+10,4
равна 9,6+10,4  20 дБ:
20 дБ:
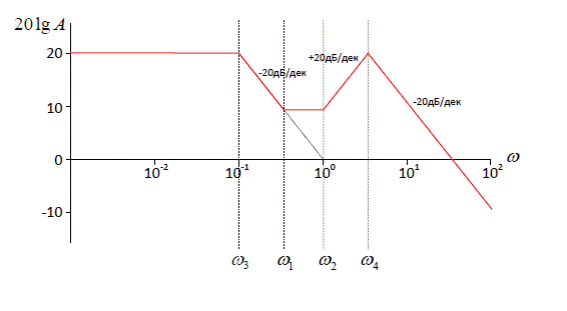
Наконец, на частоте 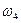 колебательное звено добавляет наклон -40 дБ/дек, таким образом, общий наклон становится равен -20 дБ/дек:
колебательное звено добавляет наклон -40 дБ/дек, таким образом, общий наклон становится равен -20 дБ/дек:
 |
1. Аналитический метод построения ЛЧХ контура с единичной ООС.
 отсюда
отсюда

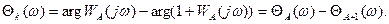
2. Построение ЛЧХ контура по номограммам замыкания (Никольса).
Пусть амплитудно-фазовая частотная функция замкнутой системы имеет вид
(1)  причем
причем  ,
,
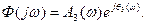
Амплитудную и фазовую частотные функции замкнутой системы Аз(w) и qз(w) можно выразить через А(w) и  разомкнутой цепи.
разомкнутой цепи.
Согласно формуле (1) имеем 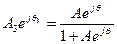
или, взяв обратные величины слева и справа, получим новое равенство 
Подставим сюда  и приравняем затем отдельно вещественные и мнимые части. Получим два равенства
и приравняем затем отдельно вещественные и мнимые части. Получим два равенства 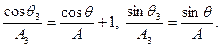
Сложив сначала квадраты этих выражений, а затем поделив одно из них на другое, получим искомый результат

 L(w1)
L(w1)
L3(w1)
q3(w1)
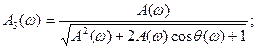

Чтобы не иметь дело на практике с этими формулами, составлены НОМОГРАММЫ ЗАМЫКАНИЯ.
Отложив на осях абсцисс и ординат заданные значения q(w1) и L(w1), находим значения 20lgАз(w1) и q(w1) на поле номограммы в точке с этими координатами. Таким образом по точкам строится вся частотная характеристика замкнутой системы.
Если контур с неединичной ООС, то его следует преобразовать к контуру с единичной ООС.
 где WА(jw)=WПК(jw)×WОС(jw). Тогда ЛЧХ замкнутой системы строится в два приёма:
где WА(jw)=WПК(jw)×WОС(jw). Тогда ЛЧХ замкнутой системы строится в два приёма:
вначале строятся ЛЧХ контура с единичной ООС, затем строятся ЛЧХ функции 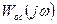 и, наконец, результирующие ЛЧХ системы:
и, наконец, результирующие ЛЧХ системы:  и
и 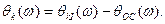
Алгоритм построения ЛЧХ:

- Строится ЛЧХ разомкнутой системы по передаточной функции
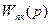 .
. - В выделенном диапазоне частот […] задаются рядом контрольных точек
 , которым соответствуют
, которым соответствуют  и
и 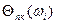 .
. - По номограмме замыкания определяются
 и
и  соответствующие
соответствующие  и
и 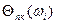 .
. - Соединив плавной кривой полученные точки в логарифмической системе координат, строят
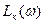 и
и  .
.
3. Построение ЛЧХ по преобразованной передаточной функции контура.
Многочлены числителя и знаменателя передаточной функции замкнутого контура или прямых параллельных звеньев преобразовываются к произведению двух - или трёхчленов, затем по методике 1 строятся ЛЧХ.
4. Построение в Matlab.
|
|
|
|
|
Дата добавления: 2015-05-09; Просмотров: 1360; Нарушение авторских прав?; Мы поможем в написании вашей работы!