Частотные характеристики

Пример

Линеаризация алгебраических уравнений

Резервуар с жидкостью

Бак с водой приведен на рис. 1. В нижней части бака просверлено отверстие, через которое вытекает вода. Площадь сечения бака обозначим через S, а площадь сечения отверстия – через .

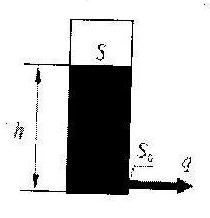
Рис. 1. Резервуар с жидкостью

Построим модель, которая связывает уровень воды в баке 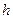(в метрах) и расход вытекающей воды 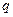(в м³/c). Эту связь можно найти с помощью закона Бернулли, который в данном случае принимает вид

,

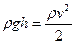где 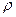- плотность жидкости (в кг/м³), м/с² – ускорение свободного падения, 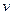- скорость вытекания жидкости (в м/с). Отсюда получаем . Учитывая, что расход воды вычисляется как 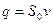, находим

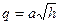, (1)

где - постоянная величина. Это статическая нелинейная модель. Статическая модель описывает установившееся состояние (статический режим), когда в баке поддерживается постоянный уровень воды и поток вытекающей воды тоже постоянный.

Линеаризовать модель – значит приближённо заменить нелинейное уравнение линейным:

,

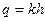где 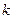- некоторый коэффициент.

Предположим, что уровень воды изменяется в интервале от 0 до 1м. Тогда один из вариантов – вычислить коэффициент как угол наклона отрезка, соединяющего точки кривой 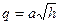на концах этого интервала. Для определённости принимаем , тогда получаем 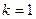(рис.2). Эта модель очень грубая и даёт большую ошибку, особенно для уровней в диапазоне от 0,1 до 0,6. Чтобы уменьшить ошибку, можно попробовать несколько изменить 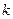(например, увеличив его до 1,2), однако точность приближения по-прежнему будет невысока, хотя и несколько лучше, чем в первом случае.

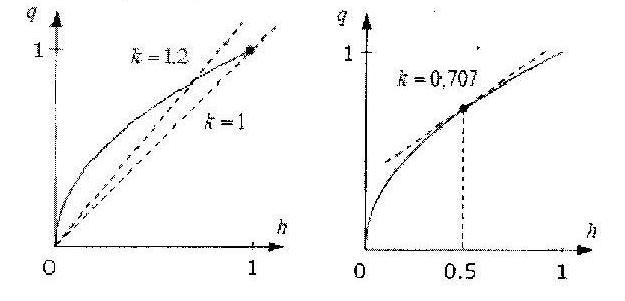
Рис. 2. Статические характеристики объекта

Теперь предположим, что обычно уровень мало изменяется вблизи среднего значения 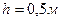. В этом случае можно применить другой подход. В этой области кривая 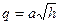почти совпадает с касательной в точке (0,5; 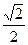), угол наклона которой равен производной

.

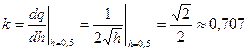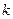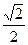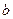Касательная – это прямая с наклоном , проходящая через точку (0,5; ), её уравнение имеет вид . Свободный член определим из равенства

,

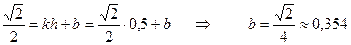так что получаем модель

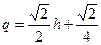. (2)

Это линейное уравнение, однако модель (2) – нелинейная, поскольку для неё не выполняется, например, свойство умножения на константу. Это легко проверить, сравнив 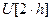и :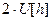

.

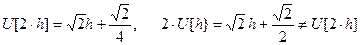Принцип суперпозиции также не выполняется.

Для того чтобы получить из (2) линейную модель, нужно записать уравнение в отклонениях от рабочей точки 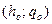, в которой определили наклон касательной. Тогда

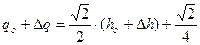. (3)

Поскольку график зависимости (2) проходит через точку 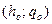, можно применить равенство

.

Тогда из (3) находим

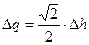. (4)

Полученное таким образом уравнение – это линейная модель объекта, записанная в отклонениях входа и выхода от номинальной (рабочей) точки 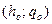. Приближённая модель (4) точнее всего соответствует объекту вблизи этой точки, а при больших отклонениях от неё ошибка значительно возрастает.

Динамические характеристики:

1. Переходная характеристика;
2. Импульсная переходная характеристика;
3. Реакция объектов и систем на типовые и требуемые по технологии работы воздействия.

Типовые входные воздействия

1. Ступенчатое (скачкообразное) воздействие.

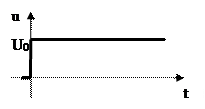
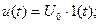если U₀=1 [размерность входного воздействия], то u(t)=1(t) – единичное ступенчатое воздействие.

Функция Хевисайда (в Matlab – heaviside(t))

.

2. Линейно-возрастающее (с постоянной скоростью) воздействие.

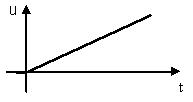
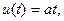где 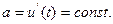u(t) – линейная функция времени.

Для систем управления движением в качестве тестового сигнала обычно используют не функцию скачка, а линейно нарастающий сигнал, поскольку электромеханические системы имеют ограниченную скорость нарастания выходной функции.

3. Параболическое (с постоянным ускорением) воздействие.

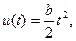где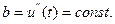

4. Синусоидальное воздействие.

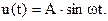
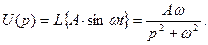
5. Воздействия в виде степенных функций времени.

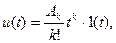изображение по Лапласу степенных функций времени имеет вид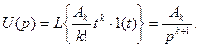

При исследовании точности работы станков с программным управлением в установившихся режимах широко используются управляющие воздействия в виде степенных функций времени.

В нормальных режимах работы управляющее воздействие в виде линейной функции времени u(t)=A×t×1(t) имеет место в следящих системах станков с программным управлением при обработке изделия с постоянной скоростью по одной или двум координатам. Управляющее воздействие в виде квадратичной степенной функции может быть, например, при обработке изделия с постоянным ускорением по одной из координат.

В ряде случаев более сложные воздействия на систему можно представить в виде суммы S степенных функций времени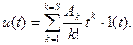

6. Дельта-функция (единичная импульсная функция, функция Дирака (в Matlab – dirac(t))).

Рассмотрим функцию

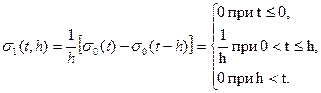
Если эту функцию трактовать как силу, действующую за промежуток времени от 0 до h, а в остальное время равную нулю, то, очевидно, импульс этой силы будет равен единице. Изображение этой функции будет т.е.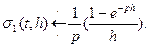

В механике и электротехнике удобно рассматривать силы, действующие очень короткий промежуток времени, как силы действующие мгновенно, но имеющие конечный импульс. Поэтому вводят функцию d(t) как предел функции s₁(t,h) при

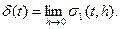
Следует иметь в виду, что d(t) не есть функция в обычном понимании. Многие авторы-физики функцию d(t) называют функцией Дирака.

Эту функцию называют также единичной импульсной функцией или дельта-функцией. Естественно положить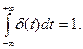

L – изображение функции d(t) определим как предел изображения функции s₁(t,h) при 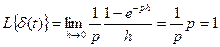(здесь воспользовались правилом Лопиталя для нахождения предела).

Частотными называются характеристики звеньев (систем) в форме графиков или таблиц, отображающие изменение амплитуды и фазы выходной функции (т.е. реакцию) звеньев или систем относительно синусоидального входного воздействия в установившемся режиме при изменении частоты от 0 до ¥.

Частотная область даёт возможность наглядно оценить динамические свойства системы:

● Резонансные;

● Свойства в установившемся режиме;

● Полосу пропускания;

● Усилительные свойства в различных областях частот.

Для линейных систем справедлив ПРИНЦИП СУПЕРПОЗИЦИИ, который можно сформулировать следующим образом.

Реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности.

Это позволяет ограничиться изучением систем только с одним входом.

В качестве входных воздействий были выбраны гармонические воздействия в виду нескольких обстоятельств:

1) реально встречающиеся воздействия, как правило, могут быть представлены в виде суммы гармоник различных частот (разложение Фурье);

2) в установившихся режимах гармонические сигналы передаются линейными элементами и системами без искажений;

3) обычно не возникает затруднений в экспериментальном исследовании поведения систем.

Функцию 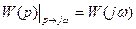называют частотной передаточной функцией (график – амплитудно – фазовой характеристикой – АФХ).

Функцию W(jw) можно представить в виде

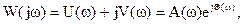
где 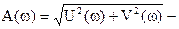амплитудно-частотная функция (график АЧХ); 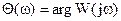- фазо-частотная функция (график ФЧХ),

U(ω) – вещественная частотная функция (график – ВЧХ),

V(ω) – мнимая частотная функция (график – МЧХ).

Если то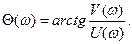

АФХ несёт информацию о реакциях на гармонические входные сигналы.

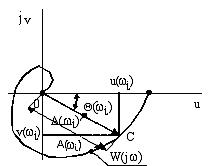
На комплексной плоскости частотную передаточную функцию W(jwι) определяет вектор 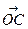, длина которого равна А(wι), а аргумент (угол, образованный этим вектором с действительной положительной полуосью) - Q(wι). Кривую, которую описывает конец этого вектора при изменении частоты от 0 до ¥ (иногда от -¥ до ¥), называют амплитудно-фазовой частотной характеристикой (АФХ).

L (w)= 20 lg A(w)= 20 lg½W(jw)½- логарифмическая амплитудная частотная функция (график - ЛАЧХ).

ЛФЧХ называют график зависимости фазового сдвига функции Q(w) от логарифма частоты lgw.

Единицей измерения L(w) является децибел, а единицей логарифма частоты в ЛЧХ – декада. Декадой называют интервал, на котором частота изменяется в 10 раз. Ось ординат при построении ЛЧХ проводят через произвольную точку оси абсцисс, а не через точку w=0. Частоте w=0 соответствует бесконечно удалённая точка: lgw®-¥ при w®0.

Белл - логарифмическая единица десятикратного увеличения мощности. Так как А(w)- отношение напряжений, токов, перемещений, то увеличение этого отношения в 10 раз будет соответствовать увеличению отношения мощностей в 100 раз, что соответствует 2 Белам или 20 дБ.

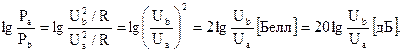
1мВт – базовая мощность в устройствах связи.

Дата добавления: 2015-05-09