Напишите основное уравнение переноса массы, энергии, импульса. Укажите ограничения его перемещения

Когда макросистема находится в равновесии, все ее термодинамические параметры постоянны по всему объему системы. Если систему вывести из равновесия и предоставить самой себе, то она постепенно вернется в равновесное состояние. При этом в системе будут протекать необратимые процессы, называемые процессами переноса. Различают несколько процессов переноса в зависимости от того, какие параметры системы были выведены из равновесия. Это – процессы переноса энергии, плотности и импульса, и связанные с ними явления теплопроводности, диффузии и вязкости. Процессы переноса возникают, когда имеется градиент какого-либо параметра макросистемы по всему объему макросистемы. При этом возникают потоки параметра в сторону уменьшения параметра.

Установление равновесия термодинамических систем происходит при помощи движения молекул. Это позволяет получить общее уравнение для всех явлений переноса.

Пусть имеется термодинамическая система с концентрацией молекул, равной . Средняя скорость молекул 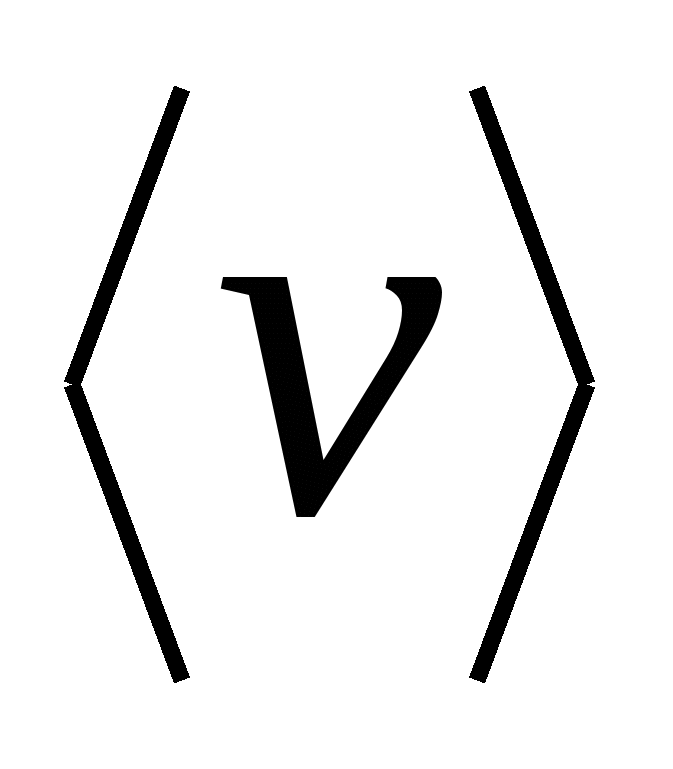. Движение молекул в такой системе будем считать полностью хаотическим для того, чтобы не было направленных токов молекул и процессы переноса обусловливались только движением молекул. Возьмем некую площадку 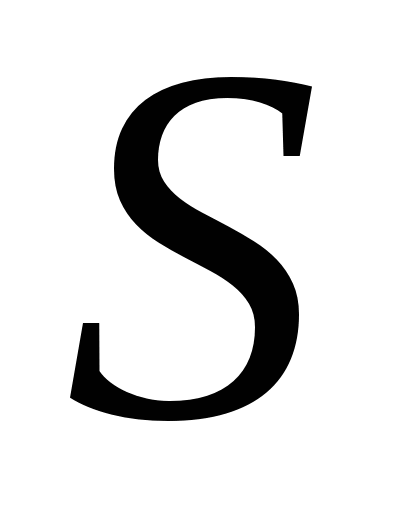единичной площади. Определим плотность потока молекул, пересекающих площадку в одном направлении. Пусть площадка располагается перпендикулярно оси . Плотность потока молекул, пересекающих площадку 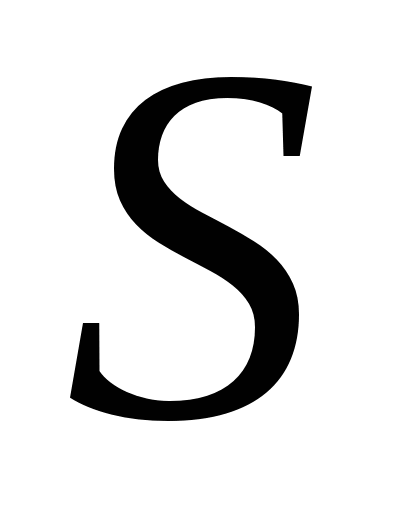в положительном направлении оси будет
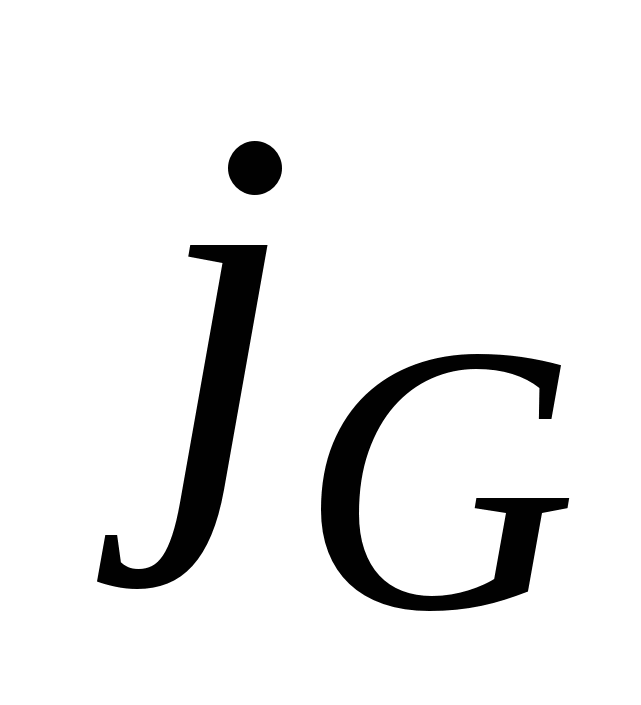Этот поток и будет переносить физическую величину , выведенную из равновесия, в сторону уменьшения ее значения. Плотность потока величины обозначим как . Предположим, что величина характеризует какое-то молекулярное свойство одной молекулы, причем молекула обладала этим свойством на расстоянии свободного пробега 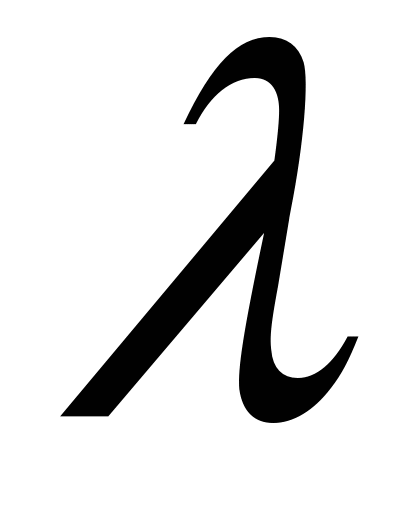от площадки 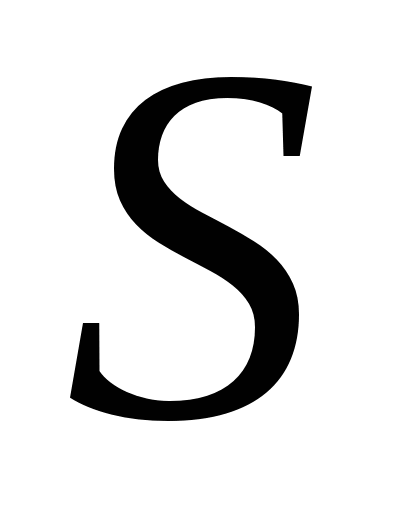. То есть последнее соударение молекула испытывала на расстоянии 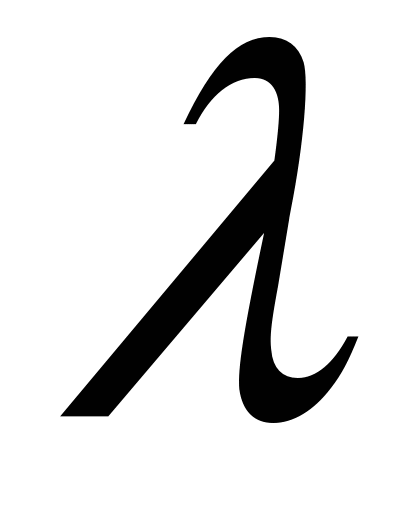от площадки .

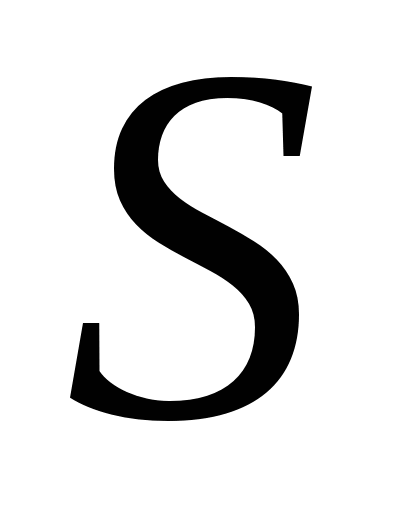Пусть величина изменяется вдоль оси , т.е. имеет место градиент . Тогда возникает поток величины в сторону ее уменьшения (рис.2.1).
Тогда общее уравнение переноса для любой величины через площадку единичной площади, перпендикулярную направлению переноса, будет следующим:
,
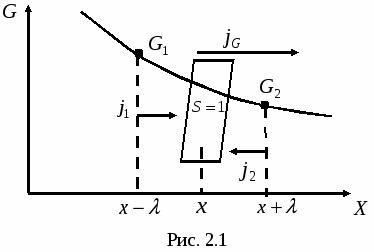
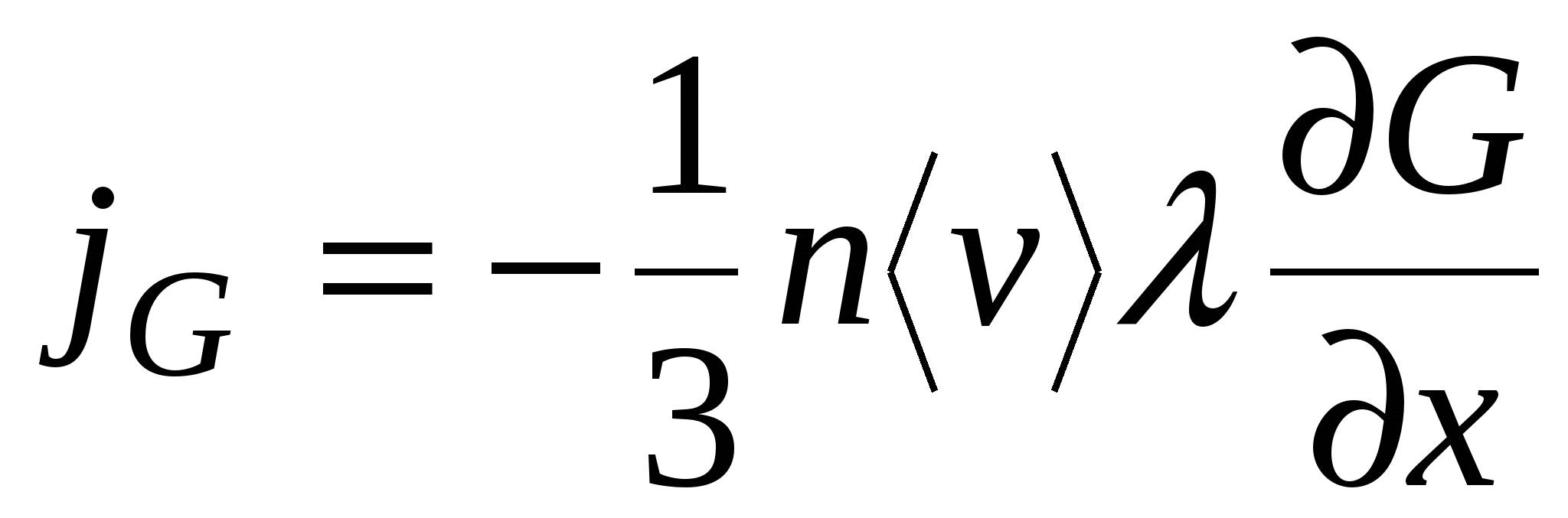где – концентрация молекул, 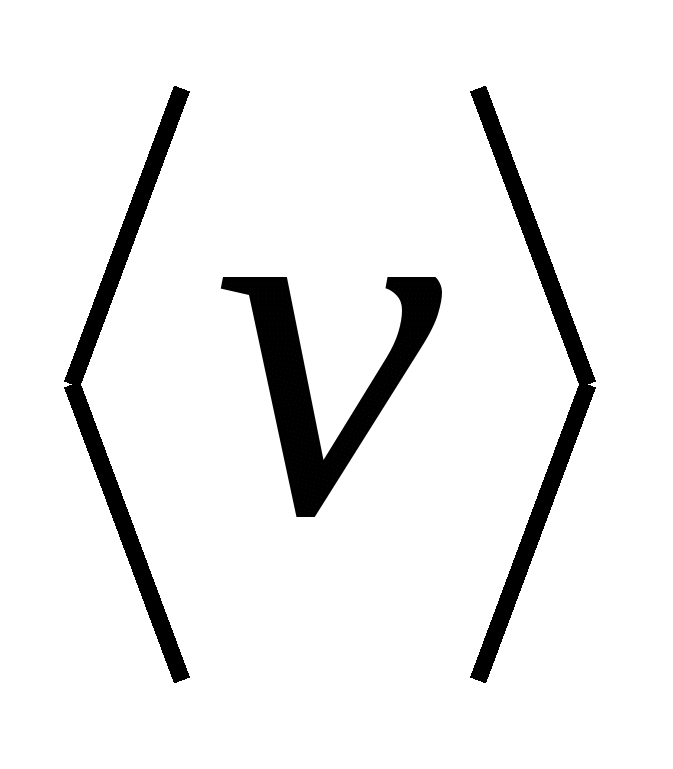– средняя скорость молекул,
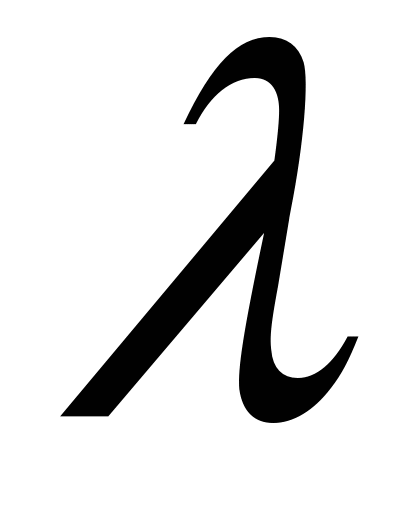– расстояние свободного пробега.
Значения этих величин берутся в сечении 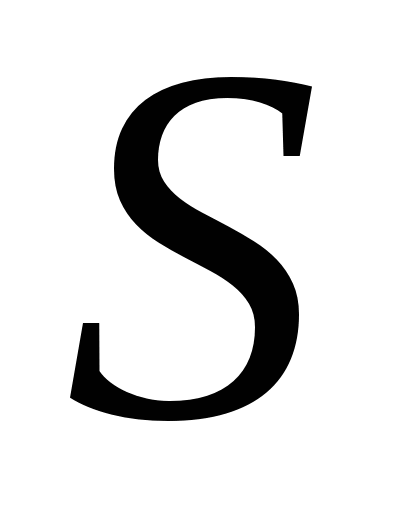. Теперь на основе общего уравнения переноса получим уравнения для переноса массы, импульса и энергии.

Процесс переноса массы обусловливает явление диффузии. Диффузия – это самопроизвольное выравнивание концентраций в смеси нескольких различных веществ. Такое выравнивание концентраций происходит из-за теплового хаотического движения молекул. Рассмотрим смесь двух газов при постоянной температуре и давлении во всем объеме сосуда. При этих условиях не будет газодинамических потоков, взаимопроникновение молекул будет обусловлено только тепловым движением. Суммарная концентрация 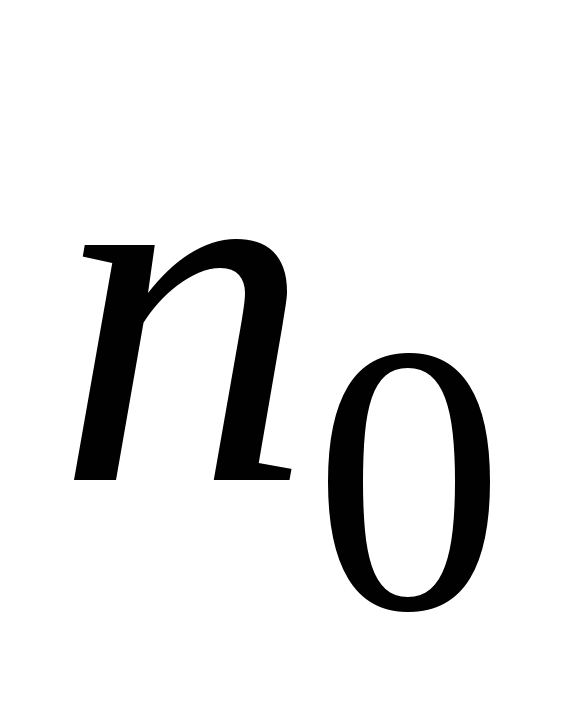обеих компонент не изменяется в зависимости от координаты по оси . От координаты зависят концентрации обеих смесе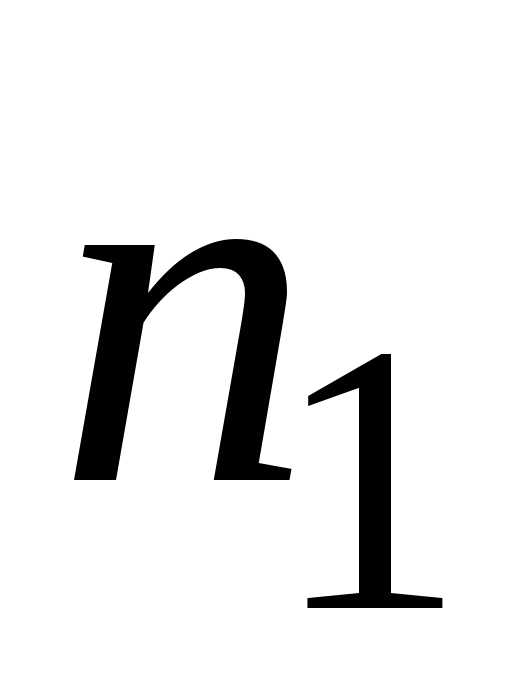й ( и 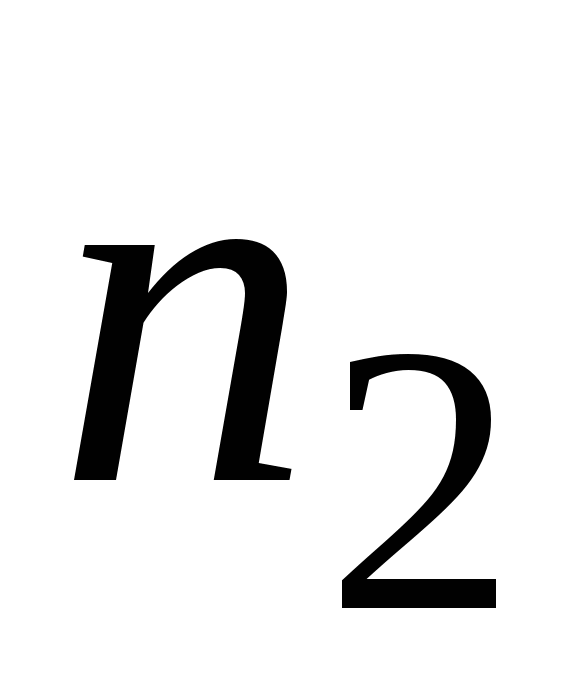). То есть возникает градиент концентрации одной из компонент, что служит причиной возникновения процесса переноса массы каждой компоненты в направлении уменьшения ее концентрации (рис. 2.2).

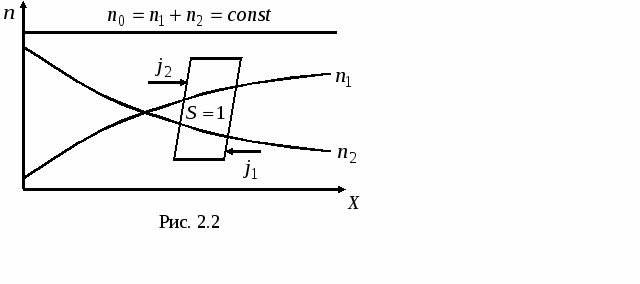
Переносимой величиной будет являться концентрация молекул одной из компонент:

Получаем выражения для потока этой величины:

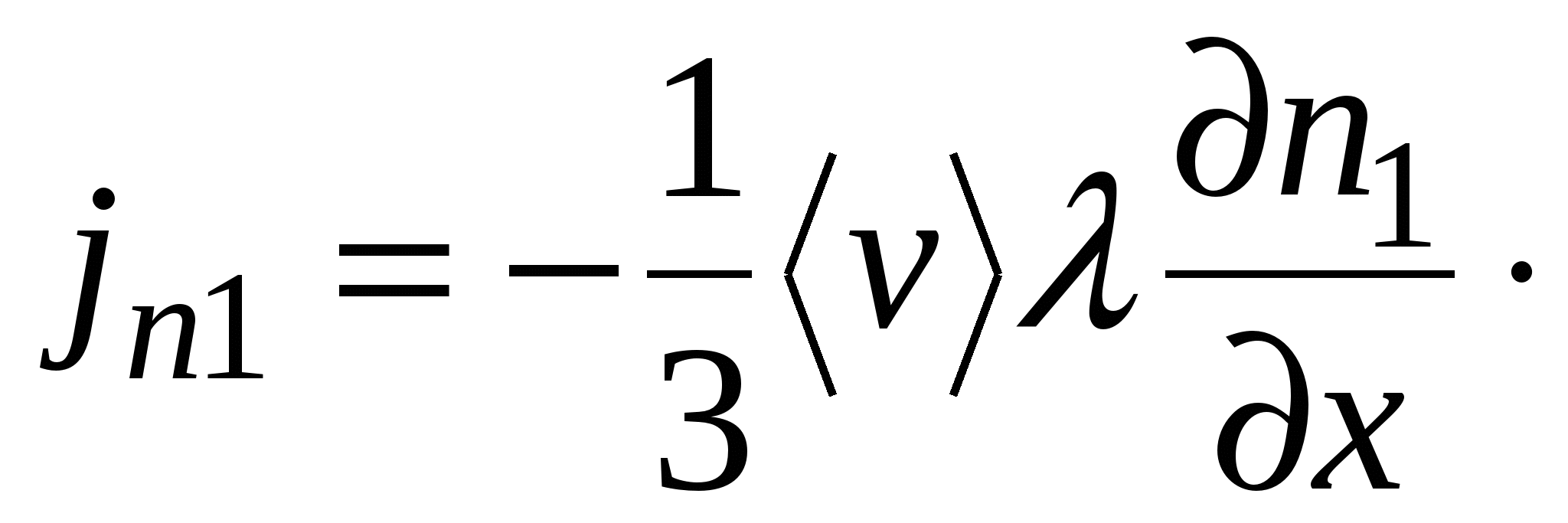
В случае, когда смесь состоит из большего количества компонент, поток -й компоненты будет выражаться тем же соотношением:
,
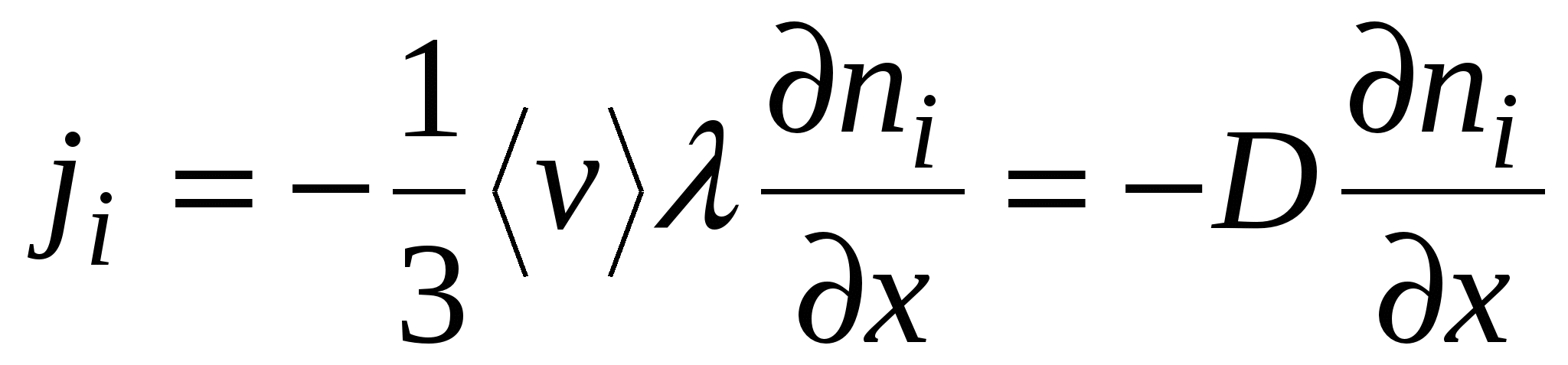где

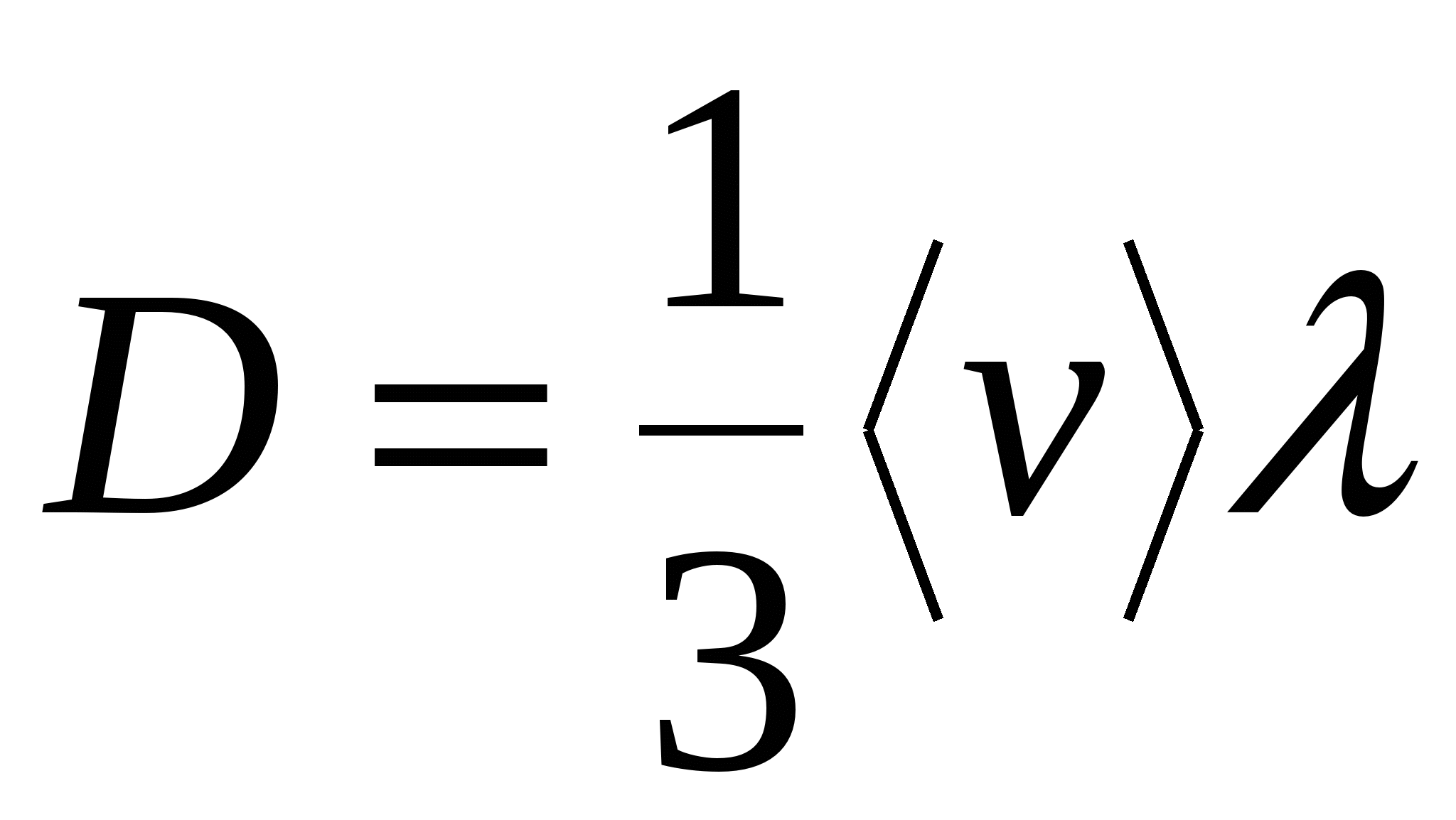
– коэффициент диффузии.

Мы получили выражение для потока через единичную площадку. При определении потока через площадку 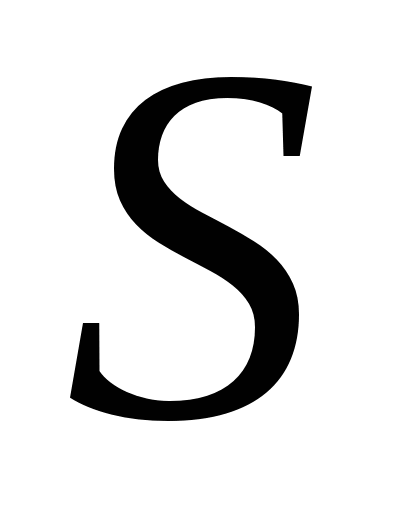, получаем соотношение, описывающее поток молекул -й компоненты:
.

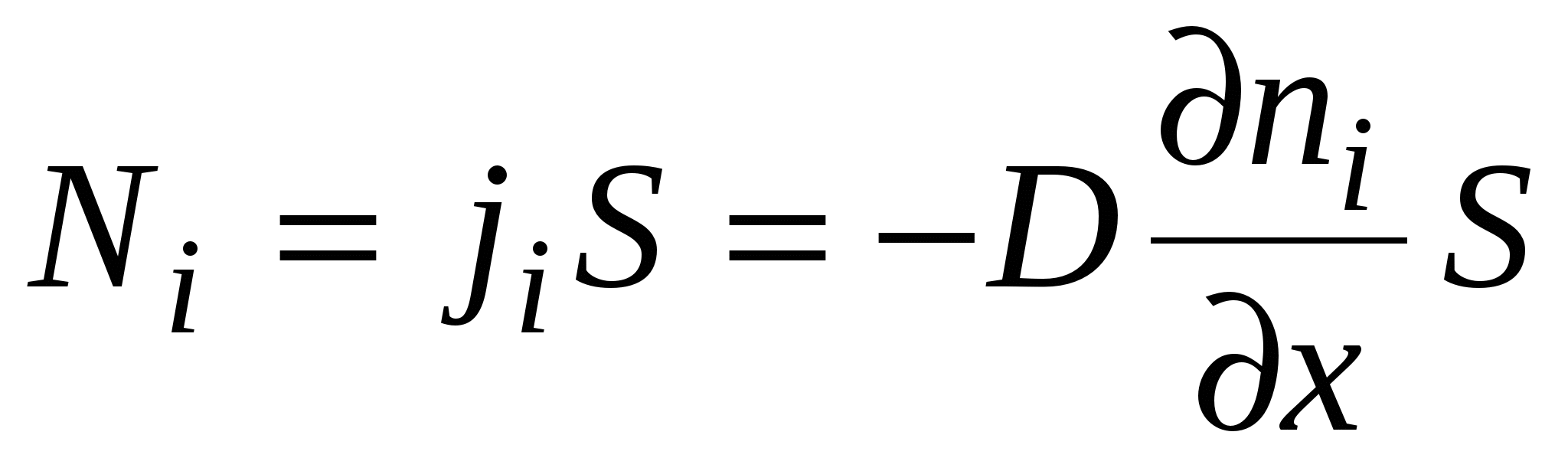Из этого соотношения можем получить выражение для потока массы -й компоненты. Для этого умножим обе части уравнения на массу 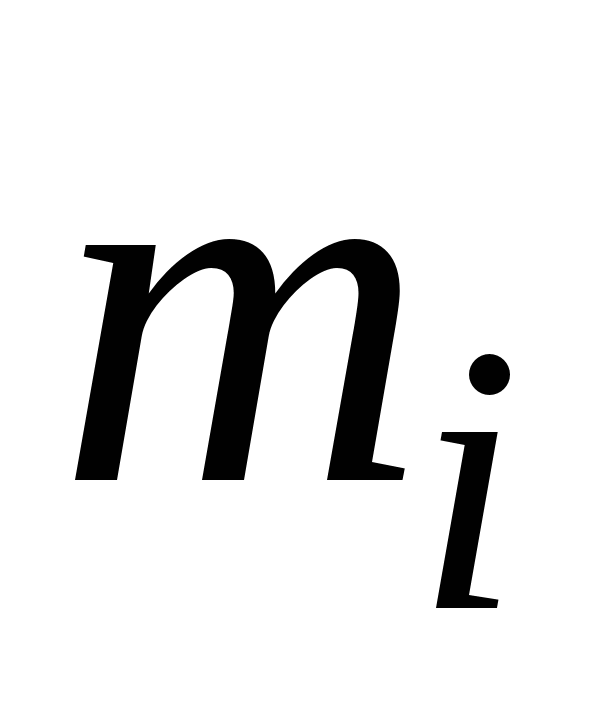молекулы -й компоненты:
,

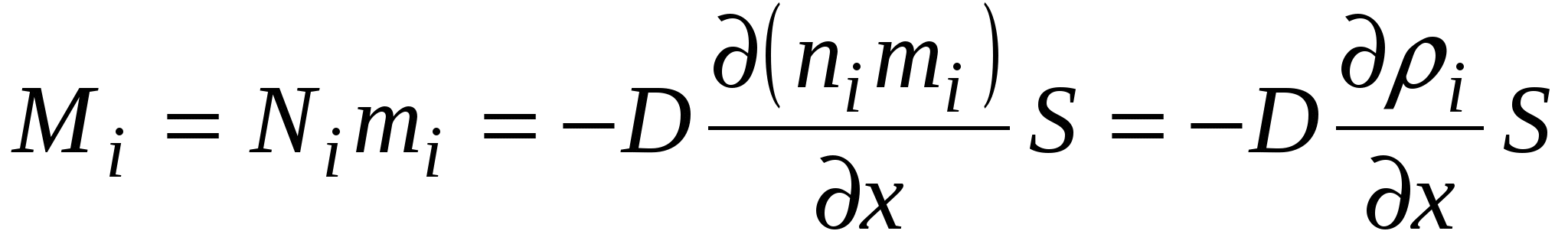где – парциальная плотность -й компоненты.

Два последних выражения были получены эмпирическим путем и носят название закона Фика.

Размерность коэффициента диффузии – . Коэффициент диффузии определяет массу, переносимую через поверхность площадью 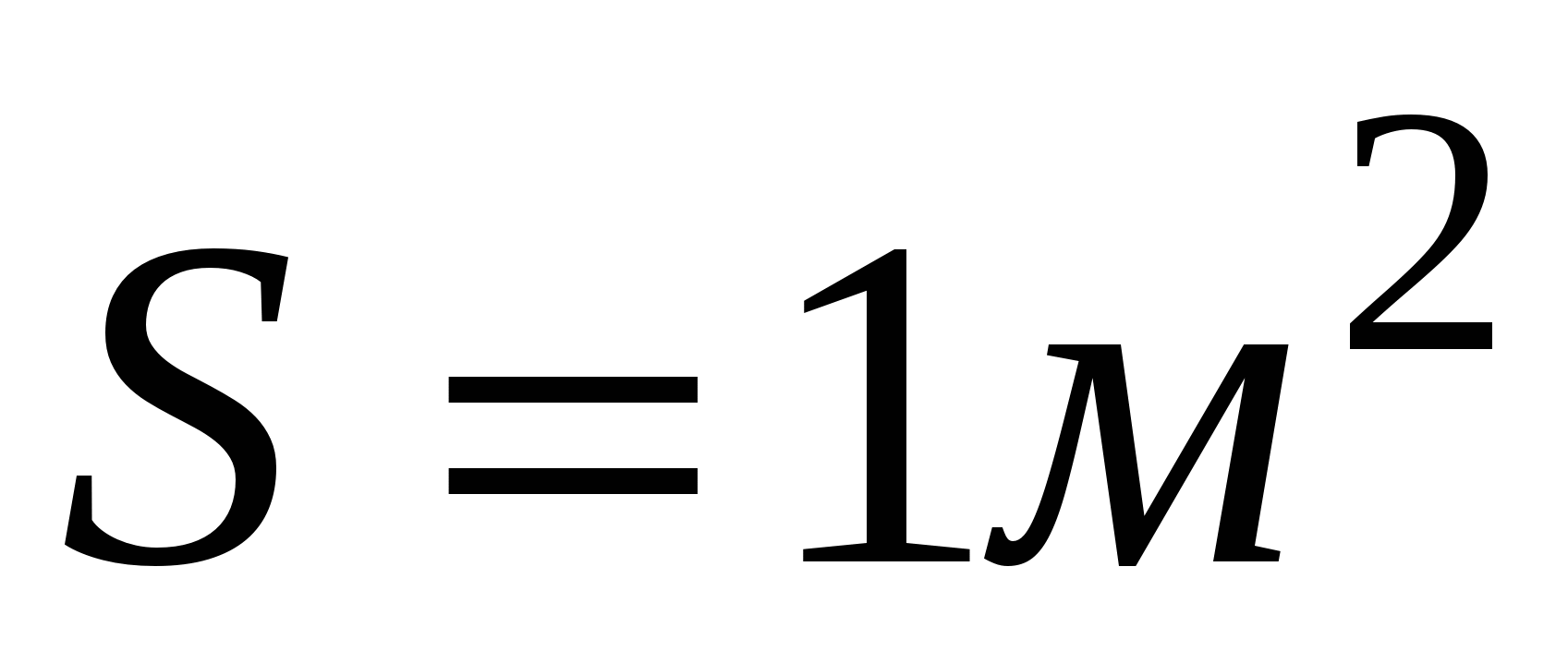за 1 секунду при градиенте плотности, равном . Коэффициент диффузии приближенно обратно пропорционален давлению, а при постоянном давлении пропорционален .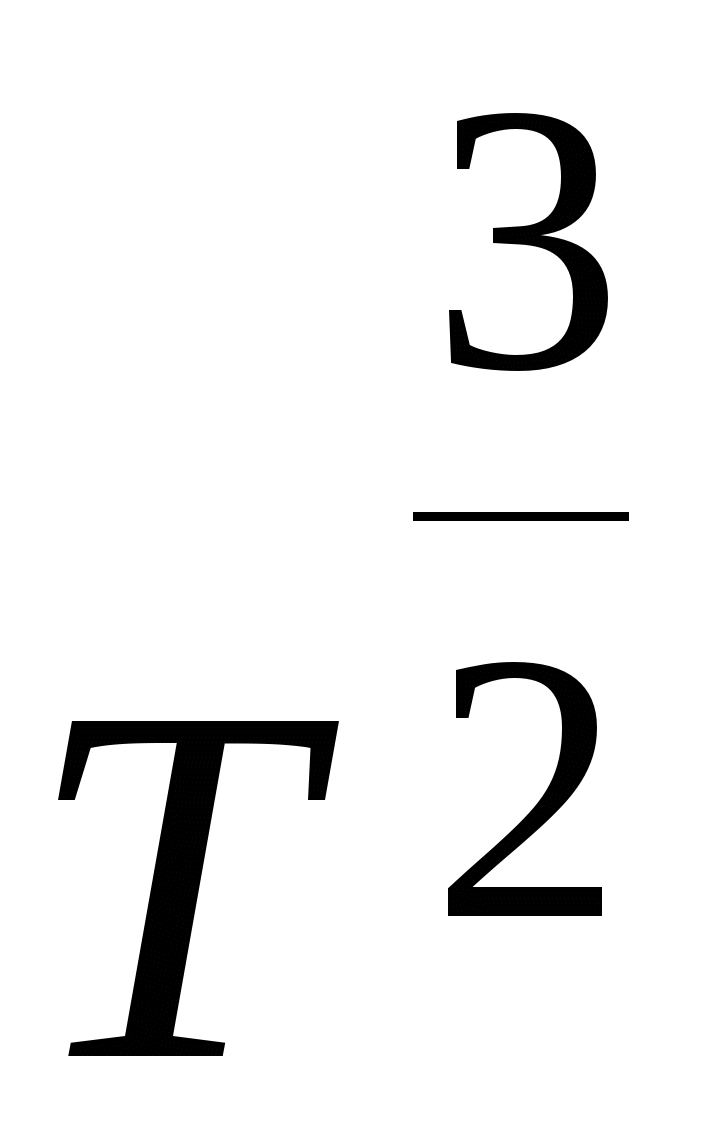

Процесс переноса импульса лежит в основе явления вязкости или внутреннего трения. Возникает это явление в тех случаях, когда на хаотическое тепловое движение молекул накладывается упорядоченное движение молекул со скоростью . Если газ или жидкость движутся в трубе, то скорости движения различных слоев газа различны. Вследствие теплового движения молекулы переходят из слоя в слой, перенося с собой импульс. При этом медленные слои ускоряются, быстрые – тормозятся (рис. 2.3).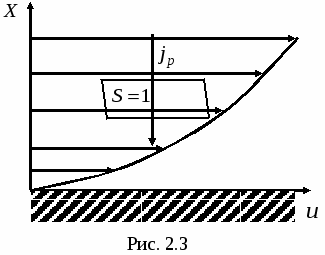

В этом случае, когда слои обмениваются импульсом, переносимая величина и будет импульсом: 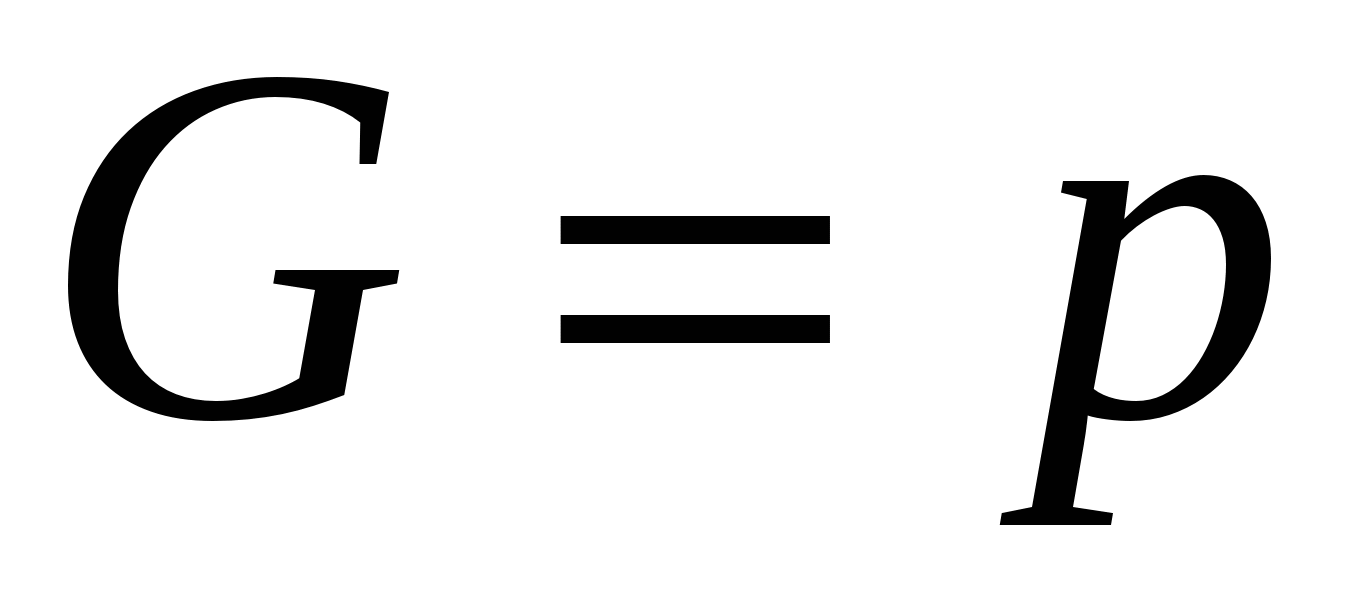. Плотность потока импульса через единичную площадку: ,

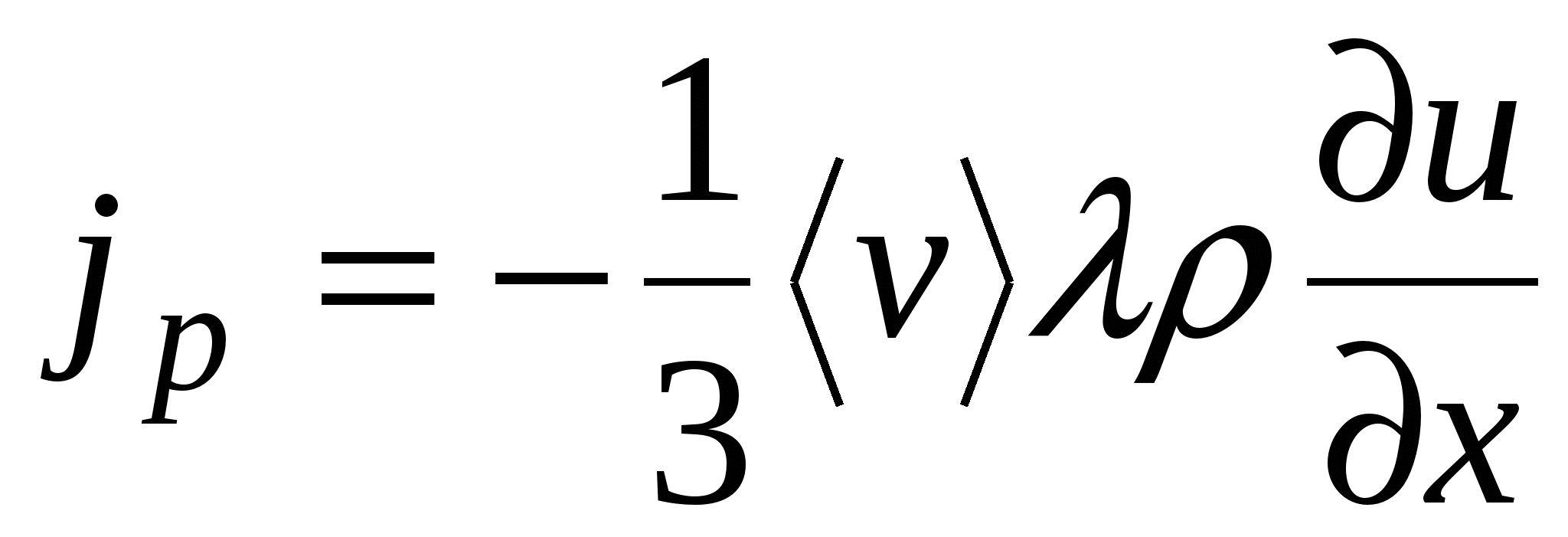где – плотность газа;

– градиент скорости в направлении оси , перпендикулярной направлению скорости

На основе этого соотношения поток импульса через площадку 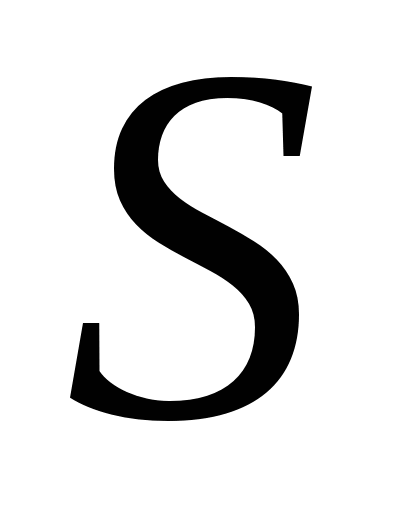может быть рассчитан как ,где – динамический коэффициент вязкости. Величина, обратная динамической вязкости, называется текучестью: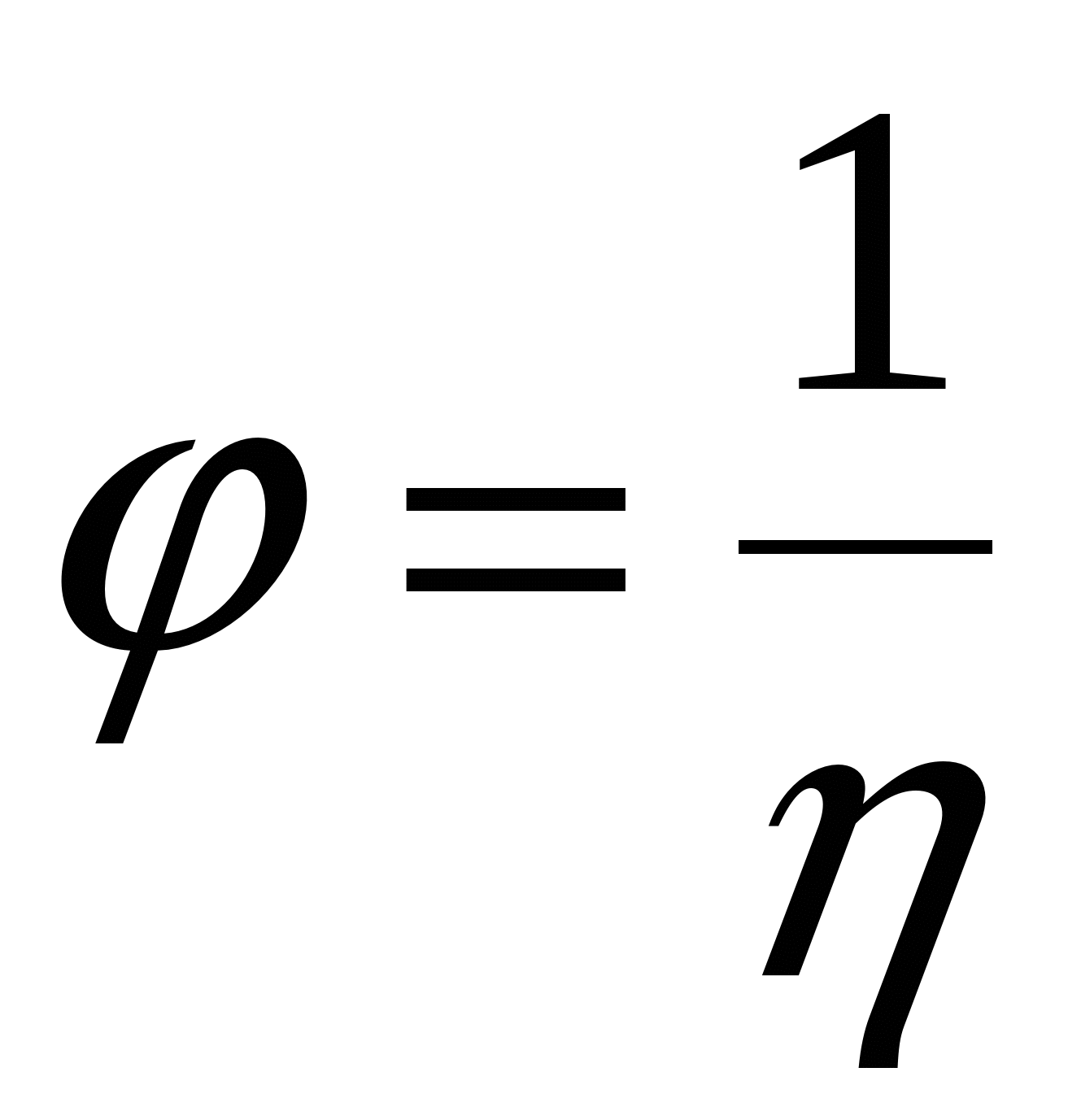

Формула потока импульса позволяет нам получить выражение для силы трения между двумя слоями жидкости или газа (формула Ньютона): 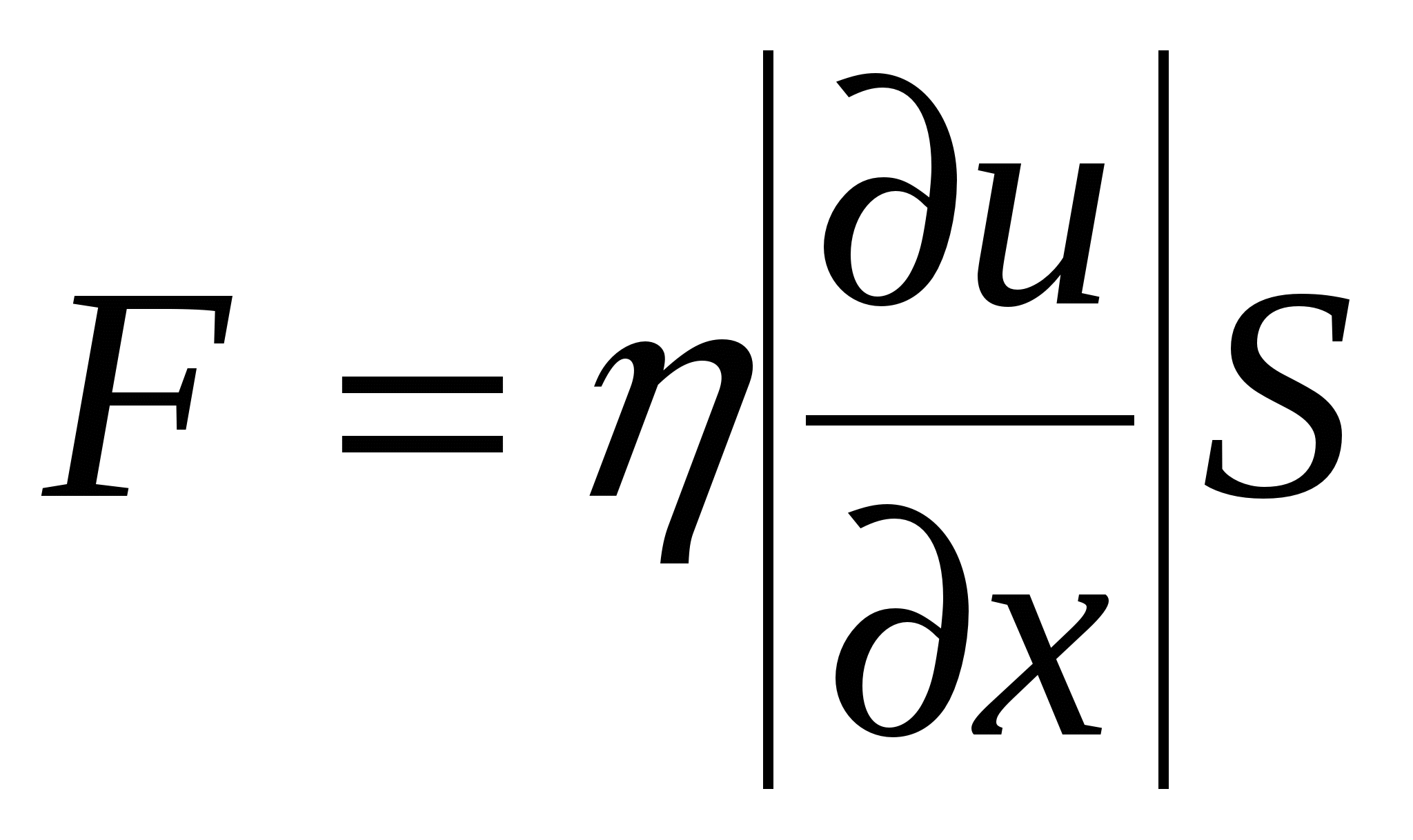. Размерность коэффициента вязкости – 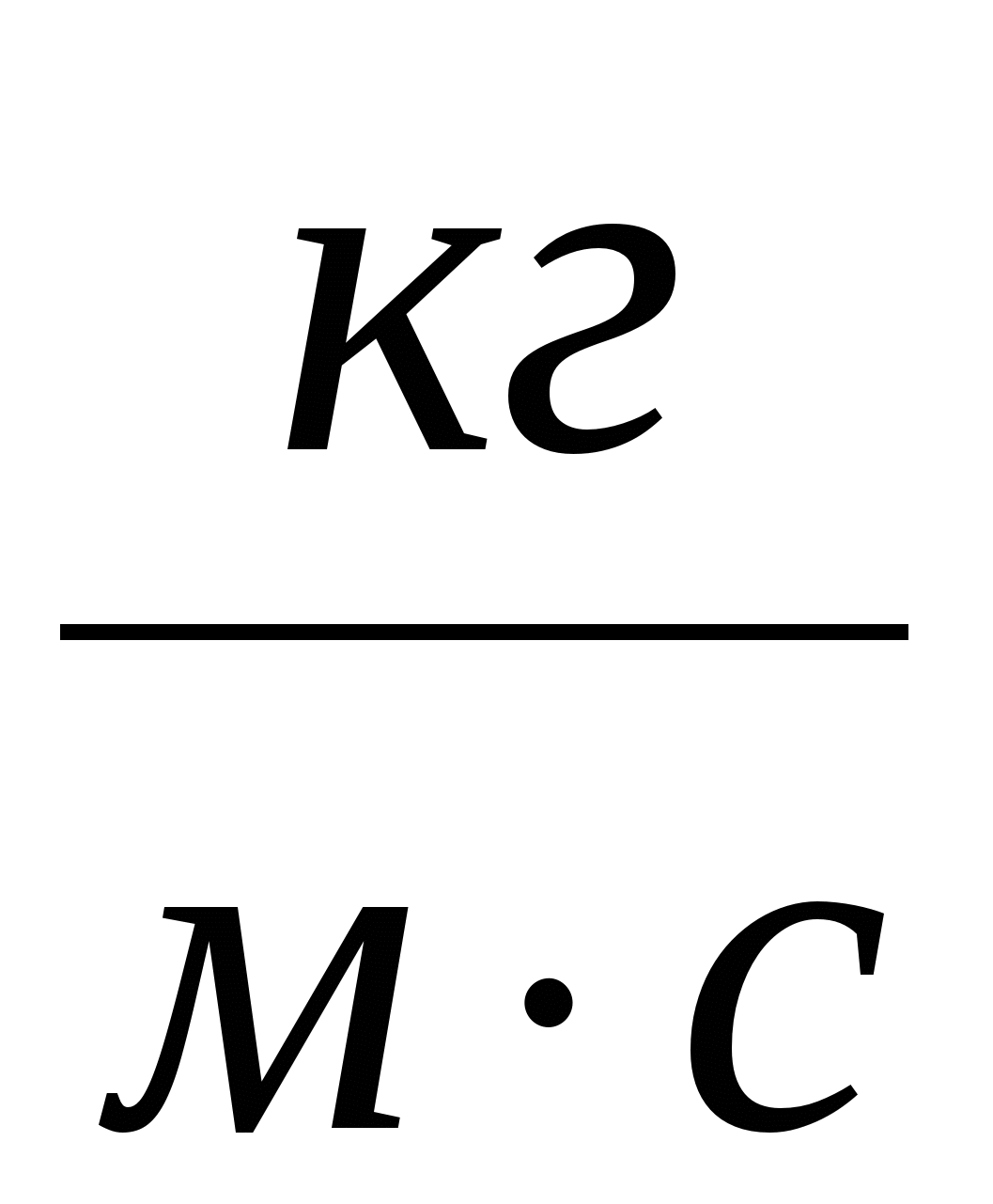. Он численно равен силе вязкости, возникающей между слоями площадью 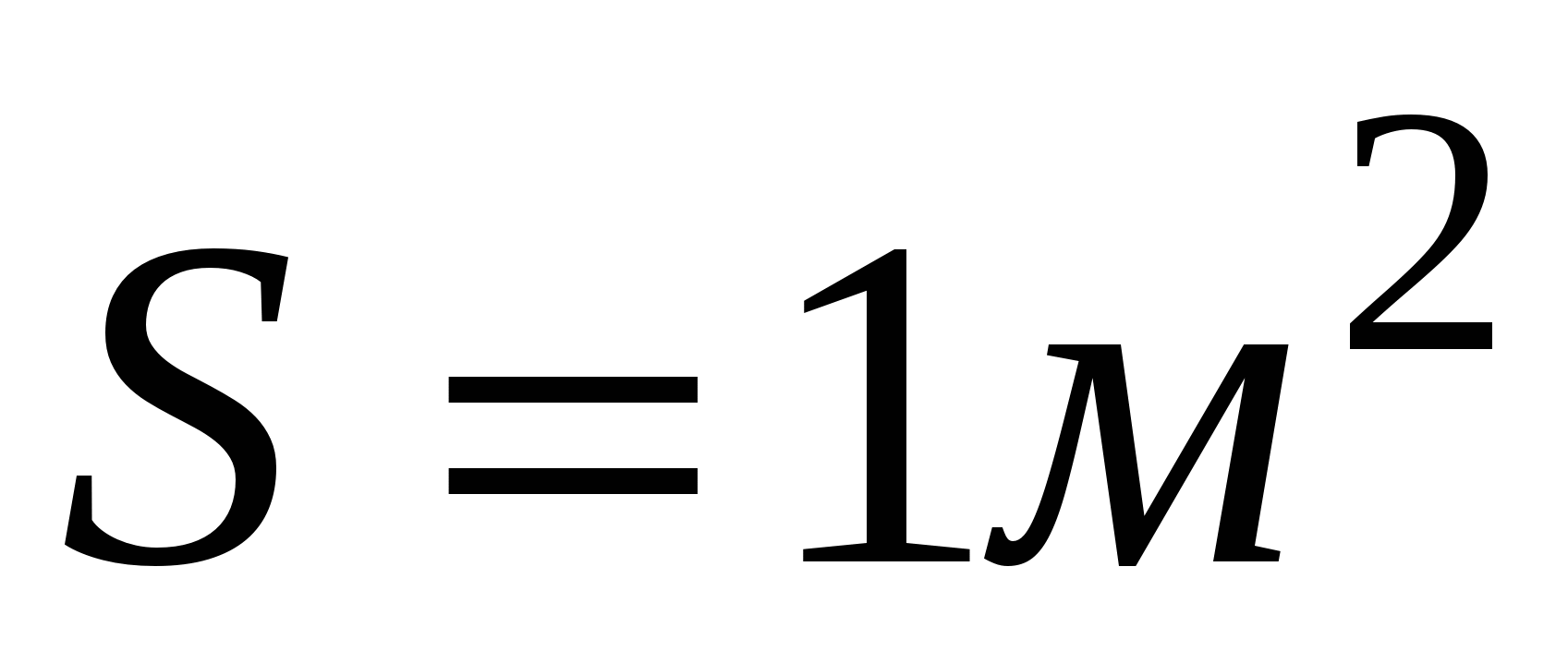при градиенте скорости, равном единице. Коэффи-циент вязкости определяет быстроту передачи импульса из одного слоя потока в другой. Коэффициент вязкости может быть получен из коэффициента диффузии: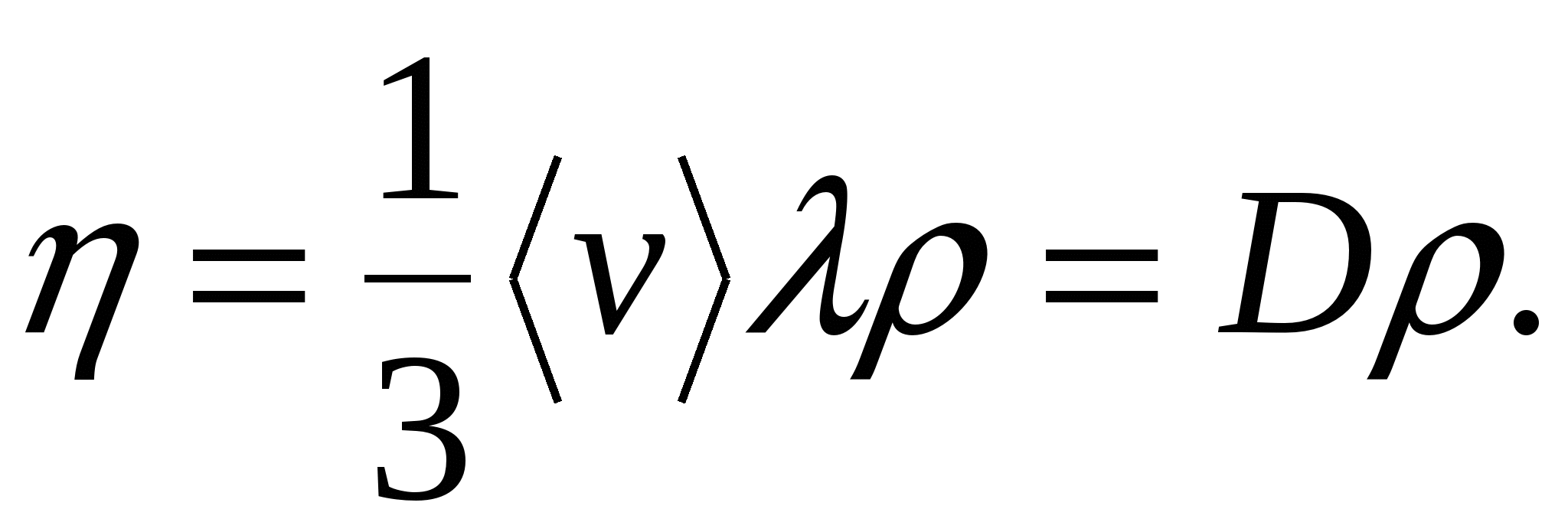

Иногда вместо динамического коэффициента вязкости применяют кинематический коэффициент вязкости , который совпадает с коэффициентом диффузии. Вязкость газов не зависит от давления и пропорциональна 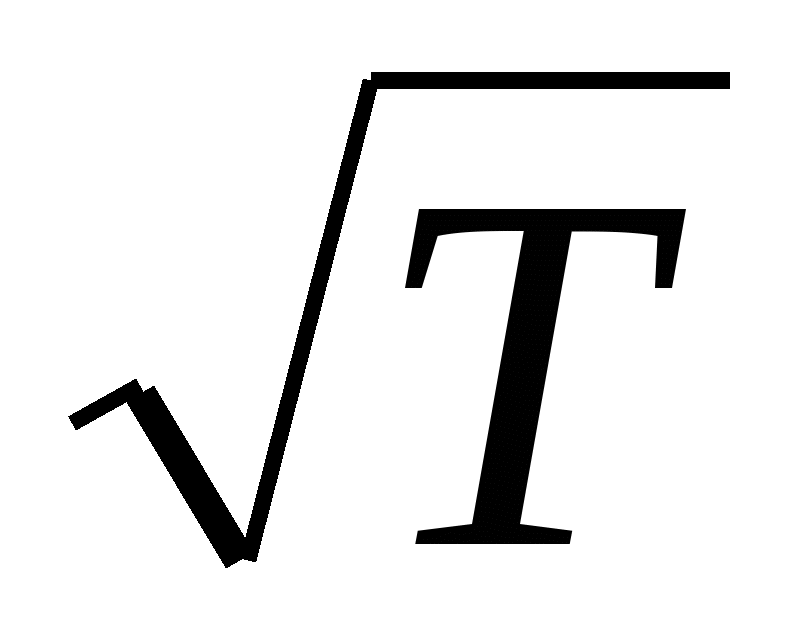. Вязкость жидкостей уменьшается с увеличением температуры. Это связано с тем, что в жидкостях молекулы находятся на сравнительно небольших расстояниях друг от друга. Поэтому их подвижность сильно ограничена межмолекулярным взаимодействием. Каждая молекула находится в силовом поле, созданном соседними молекулами. Это поле можно представить в виде большой совокупности потенциальных ям (минимумов потенциальной энергии). Потенциальные ямы расположены друг от друга на расстояниях того же порядка, что и размеры молекул. Для того, чтобы молекула перескочила из одной потенциальной ямы в другую, она должна обладать кинетической энергией, большей высоты потенциальной ямы. Поэтому коэффициент вязкости изменяется с температурой, и эта зависимость имеет вид: 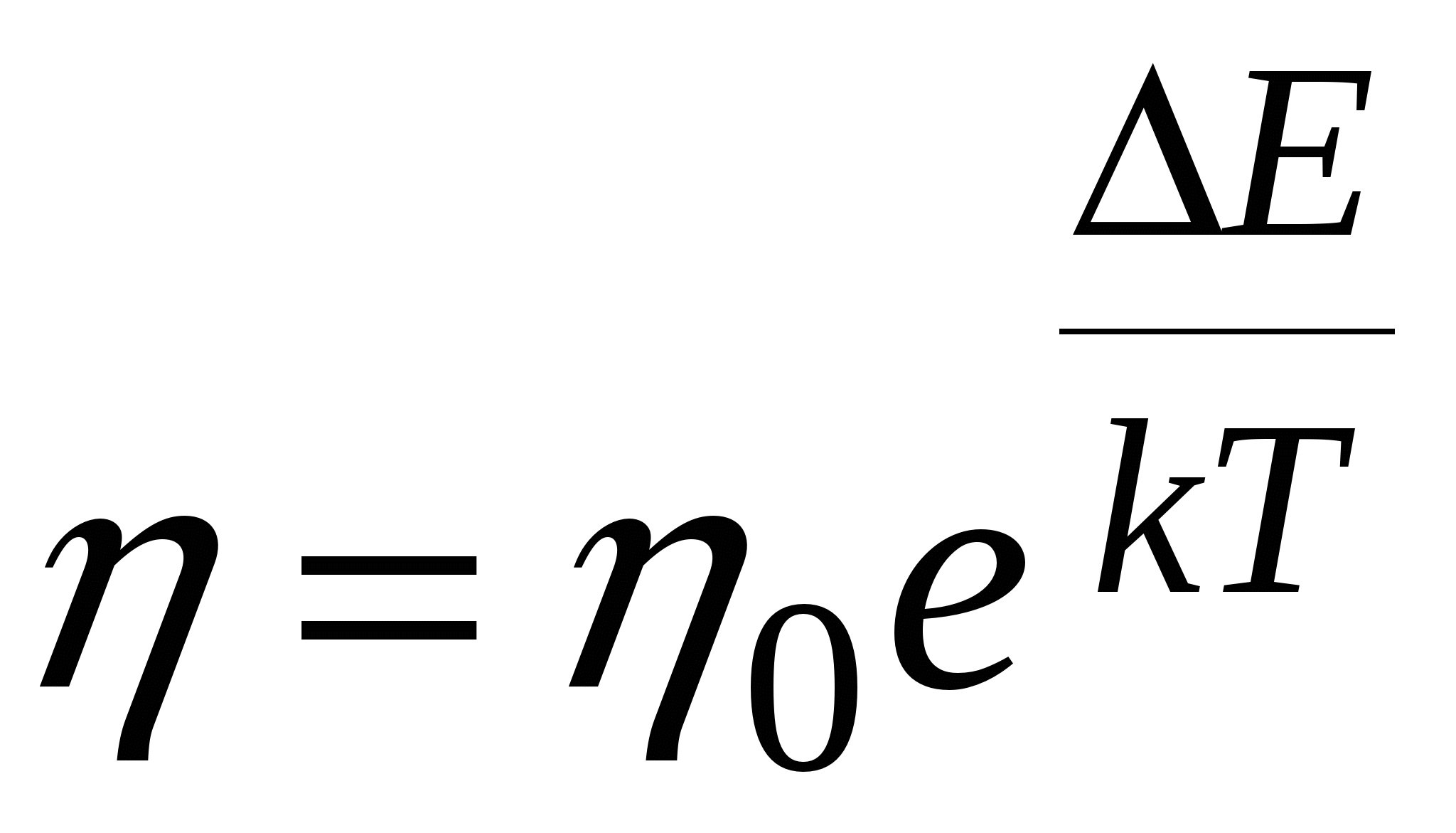, где 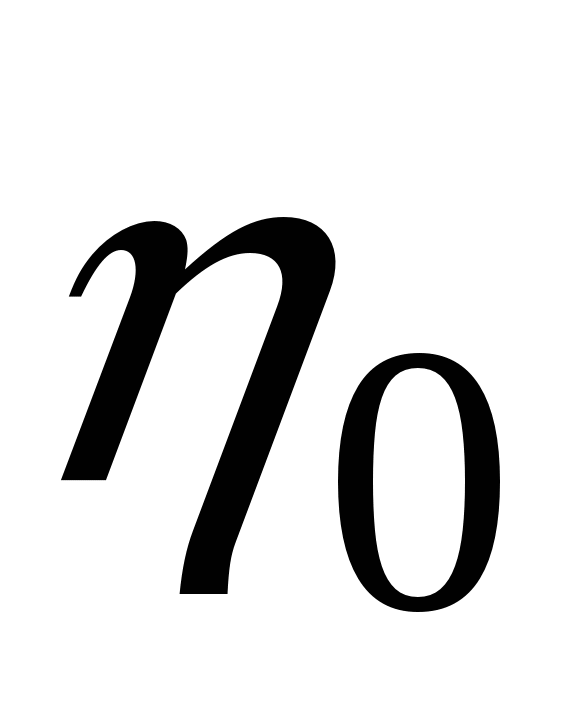– константа, слабо зависящая от температуры;

– энергия, необходимая молекуле для скачка из одного положения в другое, называемая энергией активации молекулы; 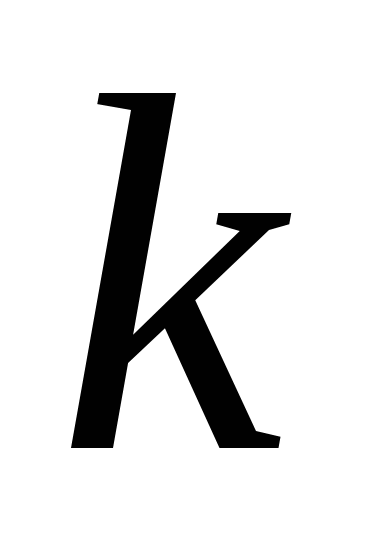– постоянная Больцмана;

– абсолютная температура.

Процесс переноса энергии лежит в основе явления теплопроводности. Если в некоторой среде возникает градиент температуры, то возникает поток тепла. В этом случае переносимой величиной будет средняя кинетическая энергия теплового движения одной молекулы 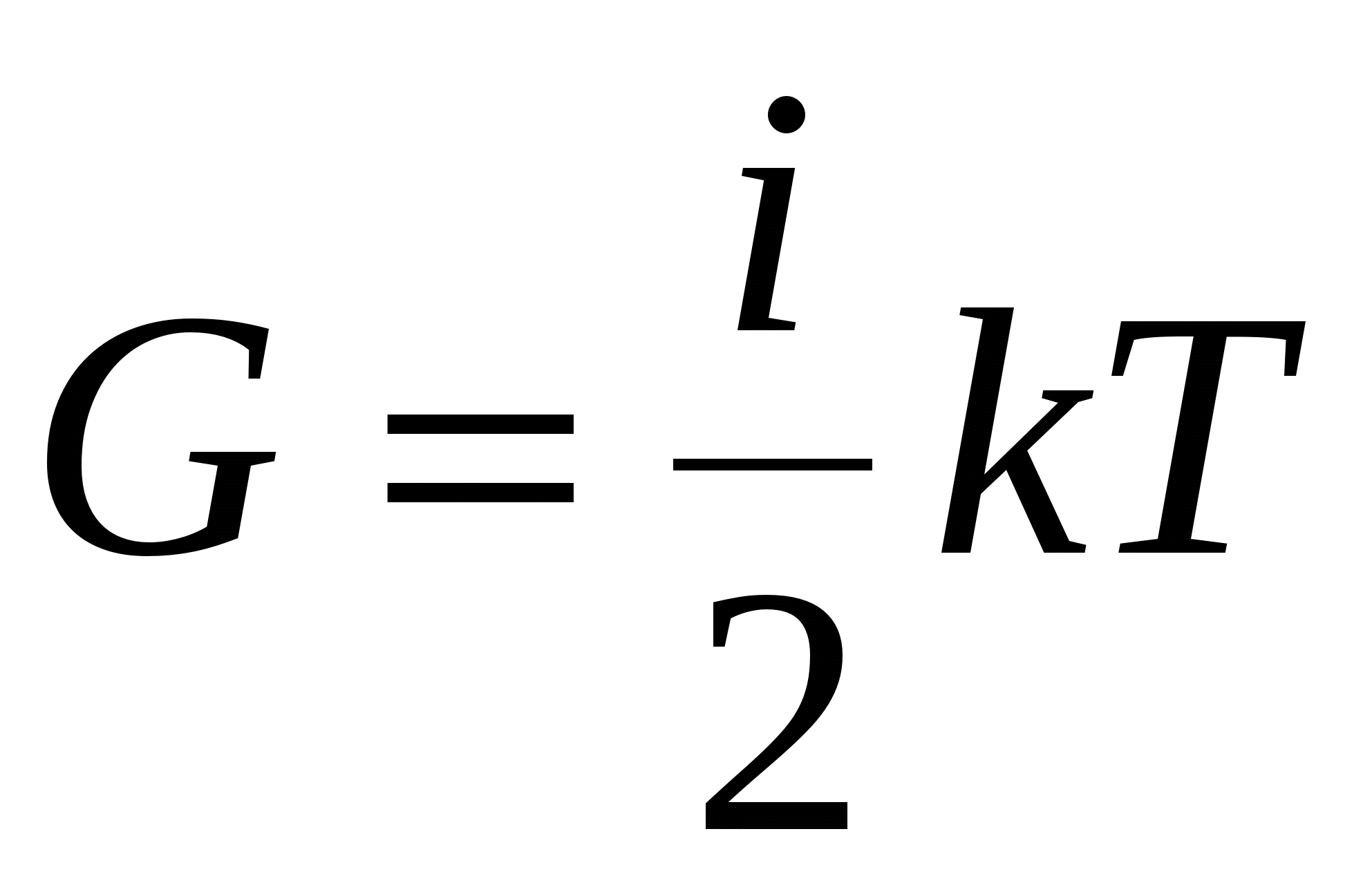. Плотность потока тепла составит 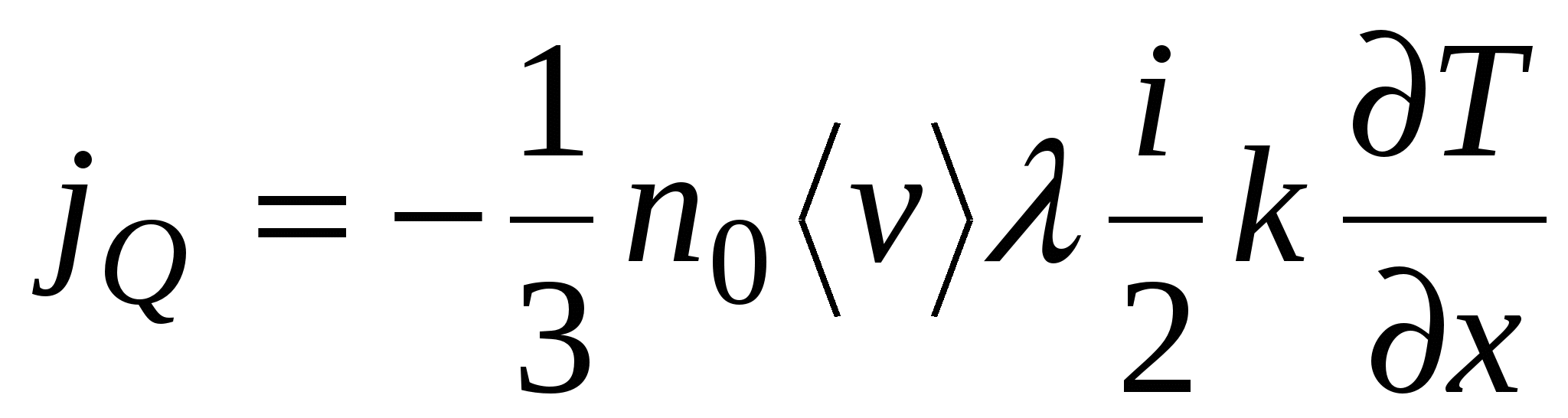Переносимую величину представим в виде: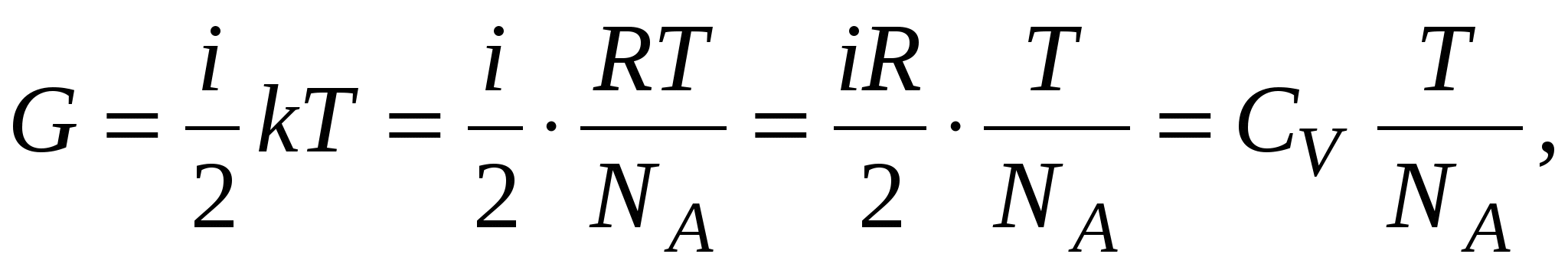

где – молярная теплоемкость при постоянном объеме. Отсюда получаем
.

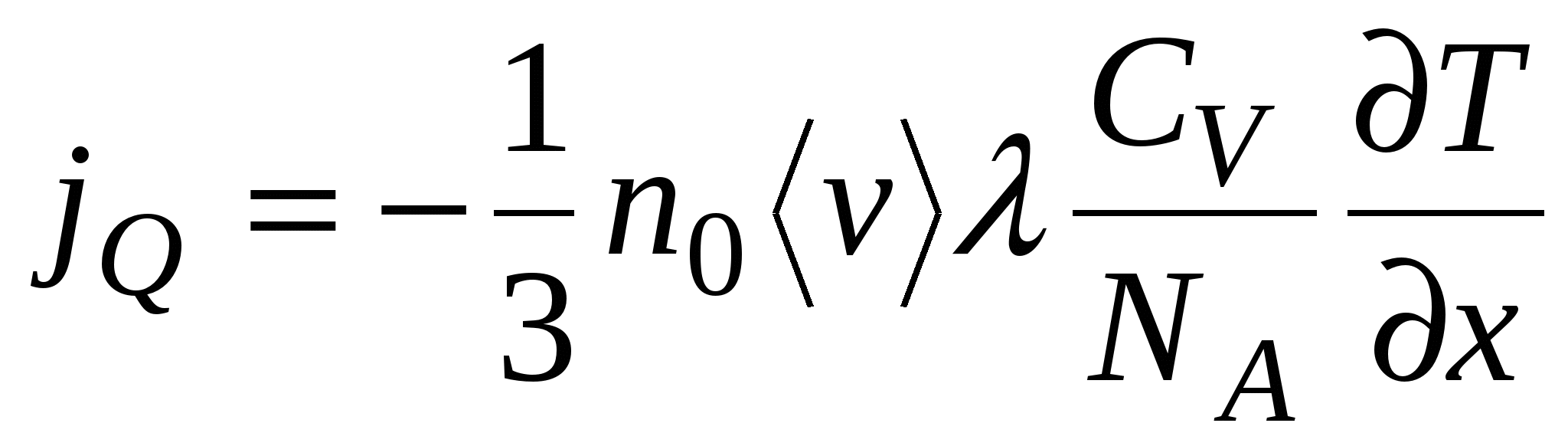Умножив и разделив на массу молекулы, и учтя, что 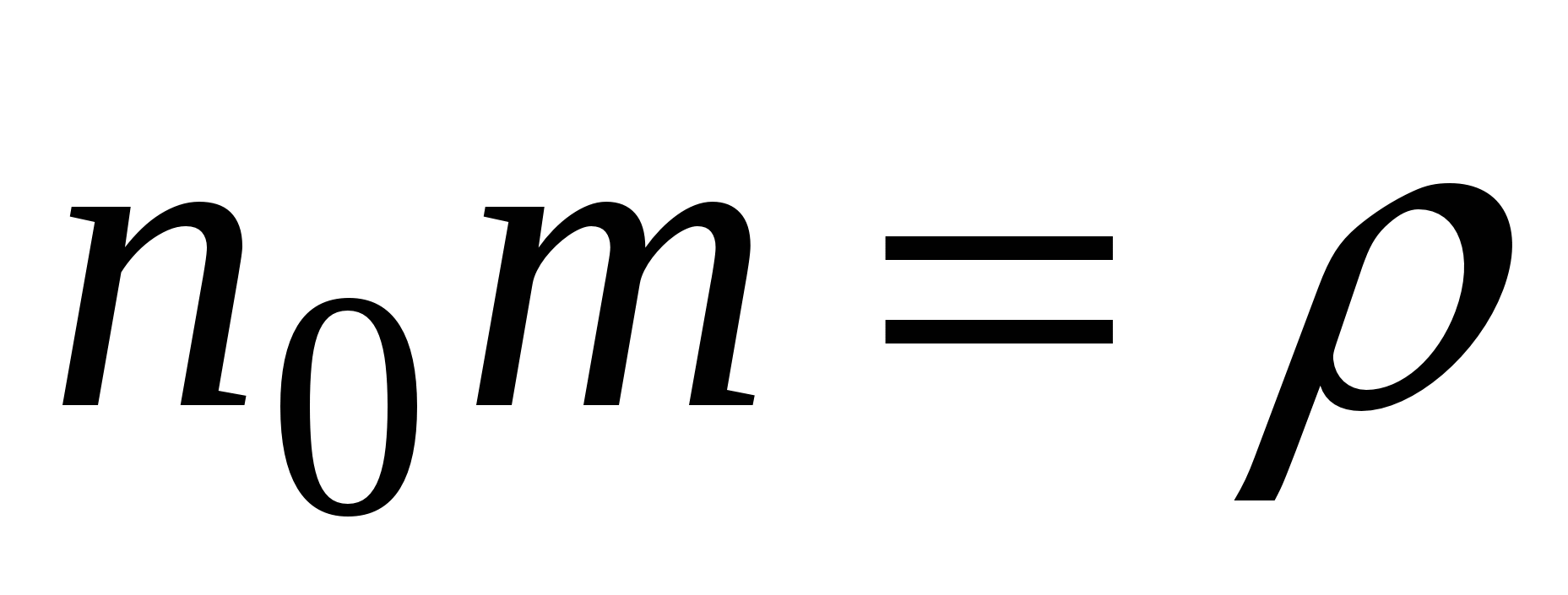– плотность вещества и 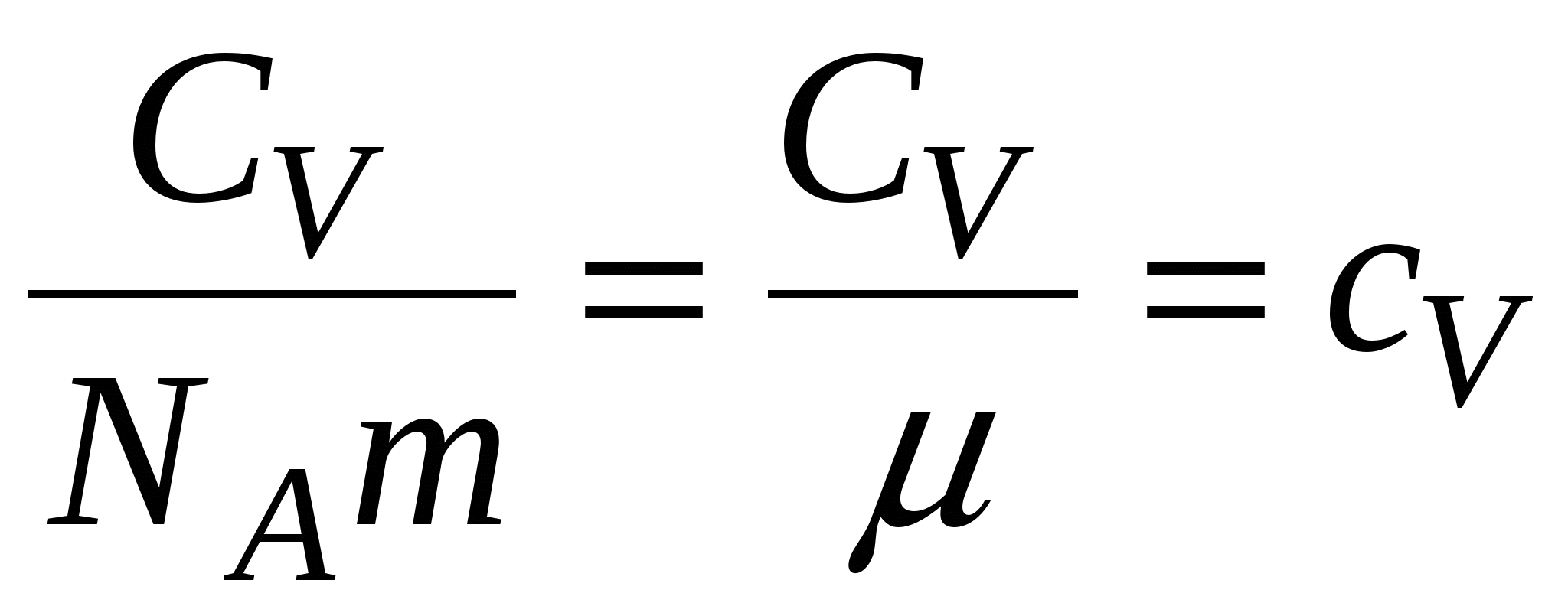– удельная теплоемкость вещества, получаем выражение для теплового потока через единичную площадь: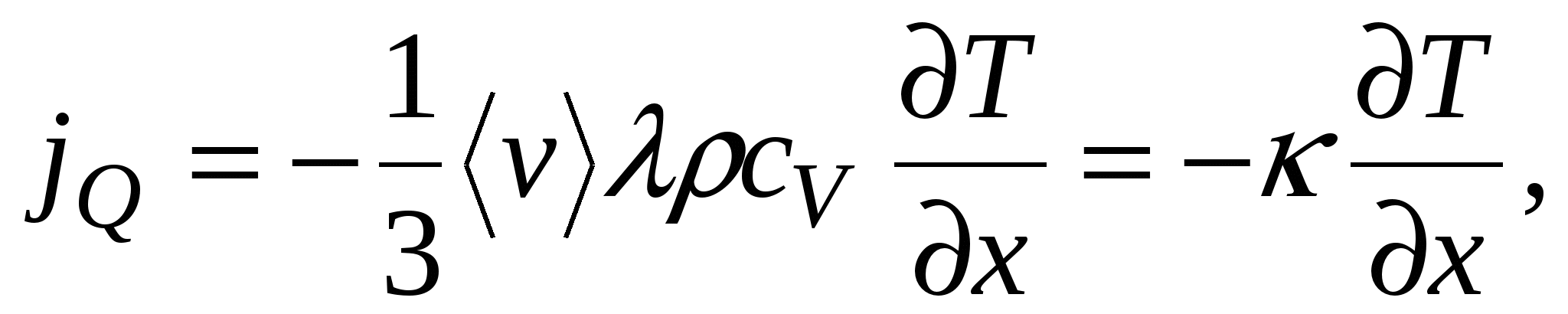

где 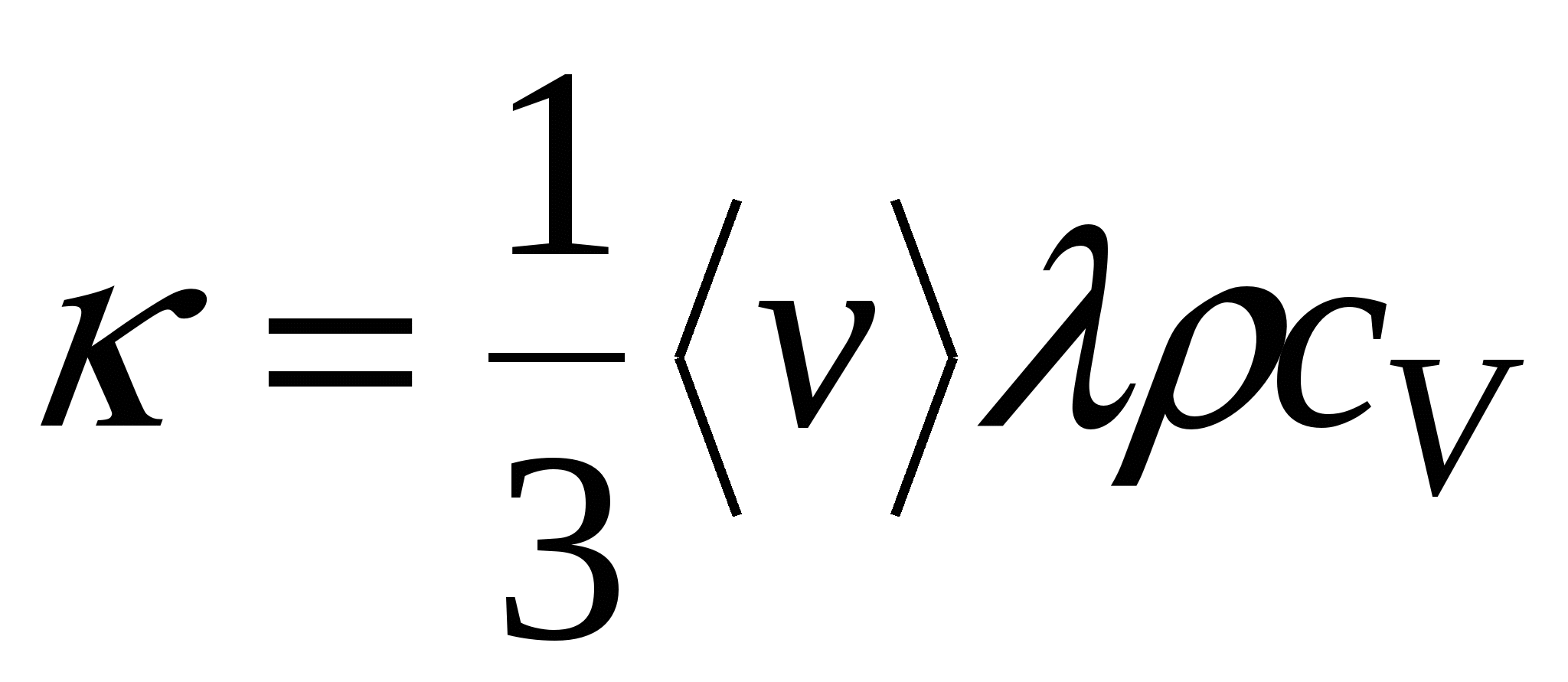– коэффициент теплопроводности. Окончательно, 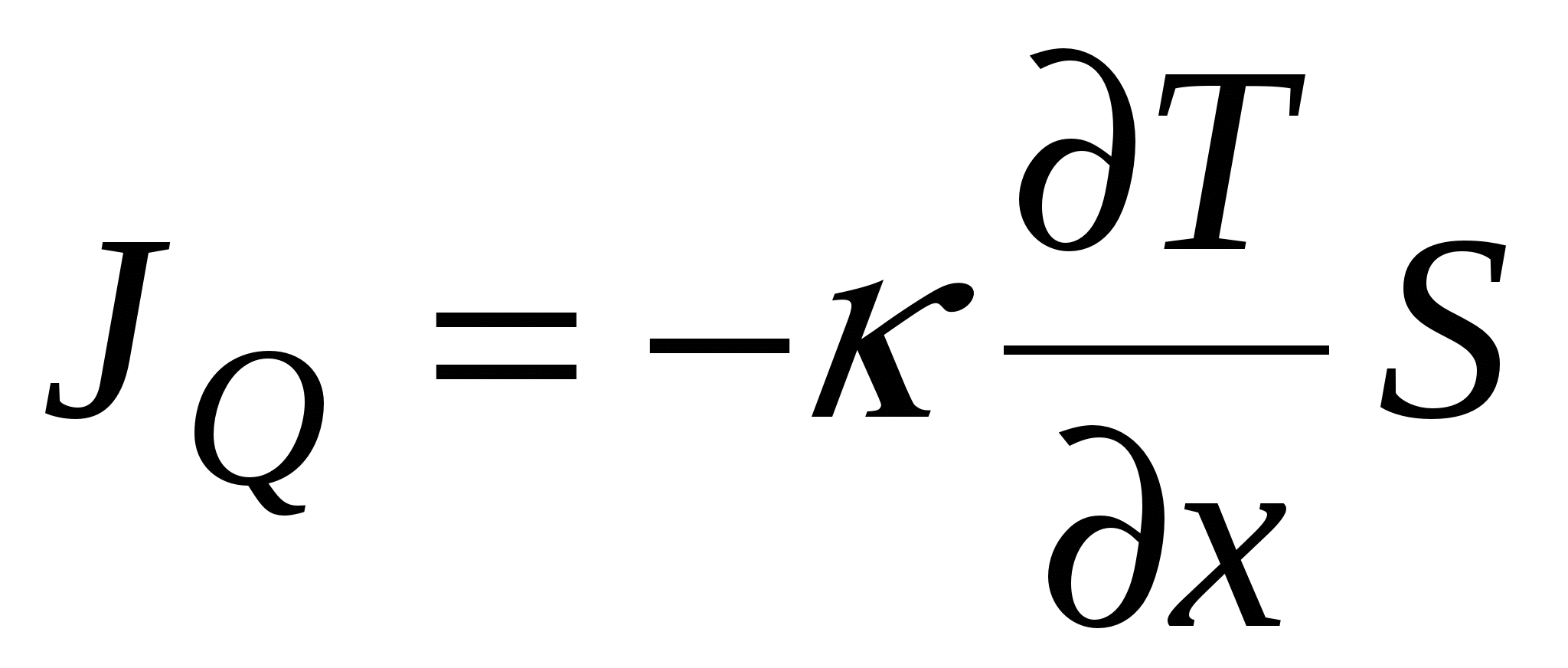. Полученное соотношение называется законом Фурье. Теплопроводность не зависит от давления и пропорциональна 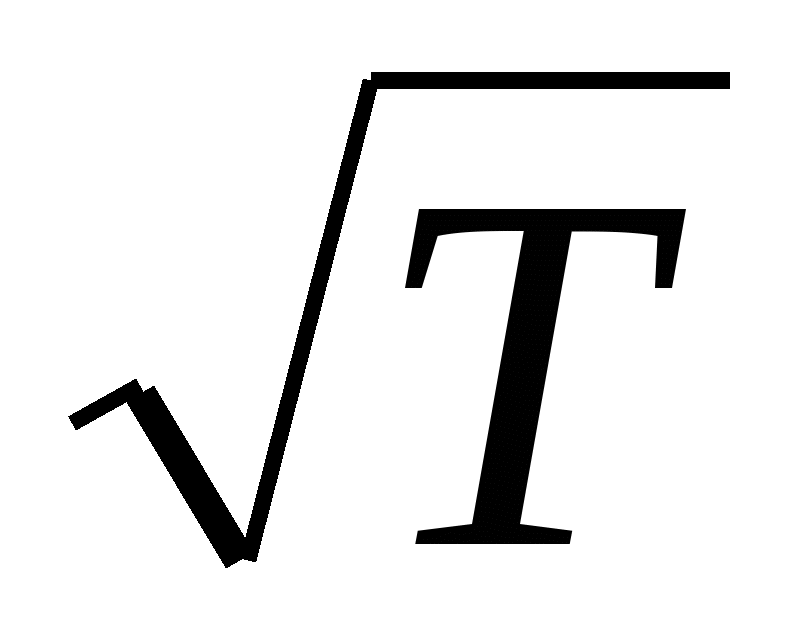Коэффициент теплопроводности может быть получен из коэффициентов диффузии и вязкости:
.

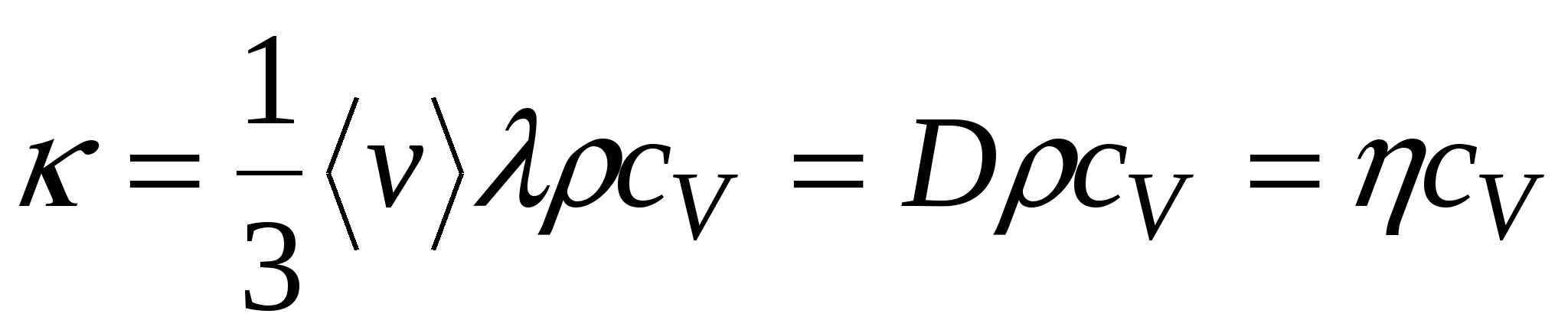Коэффициент теплопроводности имеет размерность и численно равен энергии, переносимой в виде теплоты за 1 секунду через плоскую поверхность площадью 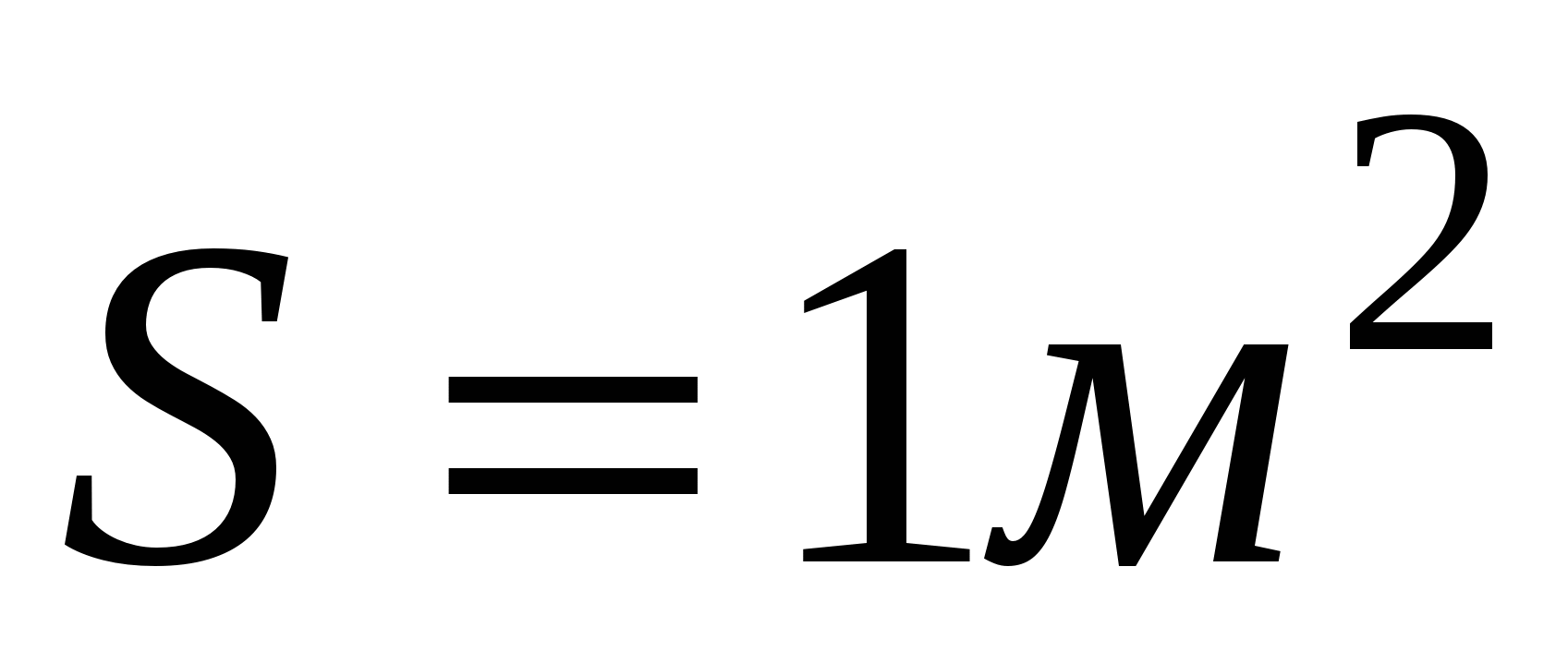при градиенте температуры, равном единице. Общими свойствами всех трёх коэффициентов является то, что эмпирически определив 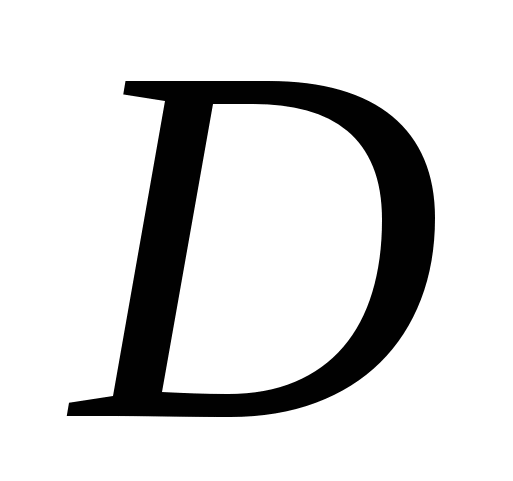, 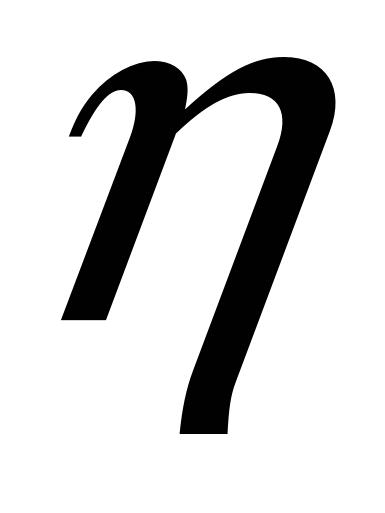и 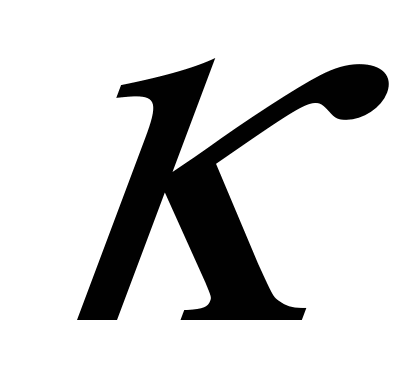, мы можем вычислить длину свободного пробега 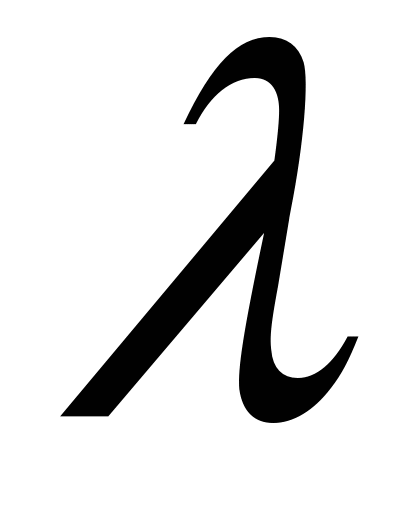и эффективный диаметр молекул .

6. Классификация основных процессов.

Классификация основных процессов и аппаратов

1) По технологическим признакам:

а). Гидромеханические процессы - подчиняются законам гидродинамики (Эйлера, Навье-Стокса, Бернулли), т.е. связаны с перемещением жидкостей и газов перемешиванием, с разделением неоднородных систем. Это - отстаивание, осаждение, центрифугирование, фильтрование, циклонирование. Движущей силой этих процессов является перепад давлений.

б). Тепловые процессы - определяются законами теплопередачи (Фурье, Кирхгофа, Ньютона). Это нагревание, охлаждение, конденсация, выпаривание различных растворов. Действие их основано на переходе тепла от одного тела к другому. Движущей силой является разность температур (зависит от гидродинамических процессов, т. е. от режима движения, скорости протекания процесса).

в). Массообменные - связанные с переходом вещества из одной фазы в другую путём массопередачи или диффузии. К ним относятся:

* абсорбция - поглощение газов жидкостью

* адсорбция - поглощение газов твёрдыми веществами

* экстракция - извлечение жидкостью вещества из другой жидкости

* ректификация - разгонка многокомпонентной смеси на составляющие компоненты

* сушка.

г) механические - связанные с законами механики твёрдых тел: дробление, транспортировка, гранулирование, сортировка.

2) По характеру протекания - организационно-технологической структуре:

а). Периодические - протекают в одном аппарате и все параметры, характеризующие этот процесс, меняются во время его протекания. При периодическом процессе необходимое сырьё загружается в аппарат и выдерживается в течении какого-то времени, затем выгружается готовый продукт. Цикл снова повторяется.

б). Непрерывные - протекают в аппарате при неизменных во времени параметрах. Отдельные стадии непрерывного процесса протекают одновременно, но в различных аппаратах.

Непрерывный процесс имеет следующие преимущества:

* возможность автоматизировать процесс

* стабильность качества выпускаемого продукта

* компактность оборудования

* возможность использования замкнутого цикла в производстве

* уменьшение эксплуатационных расходов.

в). Комбинированный - непрерывный, отдельные стадии которого проводятся периодически, или периодический, отдельные стадии которого проводятся непрерывно.

7. Классификация гетерогенных систем.

Классификация гетерогенных систем

Существует два вида систем:

Гомогенная - состоящая из одной фазы, т.е. газовой, жидкой или газообразной (химические и физические свойства одинаковы). Может быть многокомпонентной. Двухкомпонентные смеси называются бинарными.

Гетерогенная - состоит из двух и более фаз, т.е. из фазы, преобладающей в системе по количеству (дисперсионная среда), и фазы, содержащейся в системе в меньшем количестве (дисперсная среда).

Двухфазные системы могут быть следующих типов:

Г + Ж (газ + жидкость) - аэрозоли, туман, пена - образуются на поверхности жидкости пузырями газа, всплывшими в жидкости.

Ж + Г - пена или барботаш - образуется под действием архимедовой силы.

Г + Т - пыли, дымы, мелкие твердые частицы размером 0,30-70 мкм.

Ж + Т - суспензии (грубые > 100 мкм, тонкие - 0,50-100 мкм, мути < 0,50 мкм, коллоидные растворы - размеры молекул).

Грубые - молотый кофе

Тонкие - масляная краска

Мути - чернила

Коллоидный раствор - раствор желатина

Ж + Ж - эмульсии, состоящие из дисперсной жидкой системы и капелек жидкости, нерастворимых друг в друге. Обладают качеством инверсии или обращения фаз.

8. Основы гидравлики. Классификация жидкостей и газов. Силы действующие в жидкостях.

1.Основы гидравлики

Все гидромеханические процессы основаны на использовании законов гидравлики.

Гидравлика - наука, изучающая законы равновесия и движения жидкостей и газов и разрабатывающая методы практического применения этих законов в технике. Гидравлика делится на гидростатику и гидродинамику. Гидростатика описывает законы равновесия жидкостей, гидродинамика изучает законы движения жидкостей.

2. Классификация жидкостей и газов.

В зависимости от поведения жидкостей и газов под действием давлений и касательных напряжений принята следующая классификация:

1). Капельные (несжимаемые жидкости), которые не изменяют свой объем с увеличением давления (вода, масла, эмульсии, суспензии).

2). Упругие (сжимаемые) - газы, изменяют свой объем при увеличении давления и уменьшением температуры. Это видно из уравнения состояния идеального газа Менделеева - Клапейрона:

P*V = (m/M)*RT

В зависимости от поведения при движении все жидкости разделяются на три класса: идеальные, вязкие, неньютоновские.

Идеальные - у которых при движении не возникают силы внутреннего трения, т.е. отсутствует касательное напряжение. Это позволяет упрощать законы движения жидкостей.

3. Силы, действующие в жидкостях

Чтобы установить характер сил действующих в жидкостях выделим в ней объём V. На этот V будут действовать 2 рода сил: массовые и поверхностные.

Массовые - силы действующие на каждую частичку данного объёма жидкости, т.е. на единицу объёма массы жидкости. К ним относятся:

сила тяжести G = mg (H)

сила инерции F = ma (H)

Поверхностные силы – силы действующие на данную поверхность со стороны окружающей ее жидкости.   Поверхностные силы имеют две составляющие – нормальная Р и касательную Т.   Гидравлическим давлением или просто давлением в жидкости называется нормальная сила Р отнесенная к единице площади поверхности F, на которую она

центробежная сила F_Ц = mC_Ц (Н)

F_Ц = mω²r

P

F

T

G

действует:

Р = Р/F, (Н/м²)

Давление в СИ (Па), 1Па = Н/м²

На практике применяется другая система - техническая атмосфера:

1 атм = 9,81 * 10⁴ Па = 375 мм рт.ст. = 10⁴ мм.вод.ст.

Давление в данной точке жидкости называется полным или абсолютным. Различают избыточное давление и разряжение (вакуум)

Р_изб.= Р_абс.- Р_атм.

Р_вак.= Р_атм.- Р_абс.

Отношение касательной атмосферы к единице площади называется касательным напряжением.

τ = Т/F, (Н/м²) (при движении жидкости).

9. Основные физические свойства жидкостей.

Основные физические свойства жидкости

Основными физическими свойствами жидкости являются плотность, вязкость, поверхностное натяжение, удельный вес.

1) Плотность - масса жидкости приходящейся на единицу объёма

ρ = m/V, (кг/м³)

плотность несжимаемых жидкостей незначительно увеличивается с повышением давления и уменьшается с повышением температуры.

ρ _Н2О= 1000 кг/м³

ρ _возд.= 1,293 кг/м³

Плотность газовых смесей может быть определена из уравнения Менделеева-Клайперона:

ρ = m/V = PM/RT, (кг/м³)

2) Удельный вес γ - вес в единице объёма

γ = G/V, (Н/м³)

G = mg; γ = mg/V = pg

3) Поверхностное натяжение:

на межфазовой поверхности жидкости существует тонкий слой (в несколько молекул), в которых возникает натяжение, т.к. молекулы жидкости находятся на поверхности, сильнее притягиваются молекулами внутренних слоёв, чем молекулами другой фазы на межфазной поверхности.

Действие сил поверхностного натяжения проявляются в стремлении жидкости уменьшать свою поверхность. На создание новой поверхности необходимо затратить некоторую работу.

Величина этой работы, т.е. для создания единицы поверхности при постоянной температуре, называется поверхностным натяжением:

= А/F, (Дж/м²)

4). При движении жидкостей и газов между отдельными их слоями происходит молекулярный обмен количеством движения, и возникают силы внутреннего трения.

dv_х/dy – называется градиентом скорости   Величина касательных напряжений внутреннего трения выражается законом Ньютона-Петрова: t = ± μ dν/dy   μ – коэффициент динамической вязкости.

Свойство жидкости оказывать сопротивление перемещению отдельных её слоёв вследствие существования внутренних касательных напряжений называется вязкостью.

y

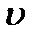
dy

x

Закон Ньютона-Петрова гласит: при движении вязкой жидкости параллельными слоями действует касательное напряжение внутреннего трения, равное произведению динамического коэффициента вязкости на градиент скорости.

μ = (Н*сек/м²) = (Па*с) = Пз = 10пз = 10⁸ спз (сантипуаз)

γ = μ/ρ (м²/с) = 10⁴ ст (стокс)

У капельных жидкостей вязкость с увеличением температуры уменьшается, у упругих увеличивается.

Неньютоновские жидкости не подчиняются закону Ньютона-Петрова.

Ньютоновские жидкости: спирт, ртуть, вода, бензин.

Неньютоновские: суспензии, растворы и расплавы полимеров, коллоидные растворы, консистентные смазки.

Описывается степенными законами: τ = μ_эф.γ (dυ_x/dу)^n-1 dυ_x/dу

Дата добавления: 2015-05-09