
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Применение производной к исследованию функций
|
|
|
|
Дифференциал функции
Операция вычисления производной называется дифференцированием.
Примеры дифференцирования:
1. 
Dy=a(x+ Dx)2 – ax2 =2ax Dx+a Dx2;
 =2ax +Dx;
=2ax +Dx; 
 =2ax, Þ(ах 2)'=2ax.
=2ax, Þ(ах 2)'=2ax.
2. 
 ;
;
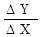 =
= 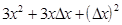 ;
;

 =3x2, Þ(x3)'=3x2.
=3x2, Þ(x3)'=3x2.
Дифференциалом функции f(х) в точке х0 называется линейная функция приращения  вида
вида 
Дифференциал функции y=f(х) обозначается dy или df(x0). Главное назначение дифференциала состоит в том, чтобы заменить приращение  на линейную функцию от
на линейную функцию от  , совершив при этом, по возможности, меньшую ошибку.
, совершив при этом, по возможности, меньшую ошибку.
Наличие конечной производной 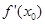 даёт возможность представить приращение функции
даёт возможность представить приращение функции  в виде
в виде

где  при
при 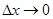 . Из этого следует, что ошибка в приближённом равенстве
. Из этого следует, что ошибка в приближённом равенстве  (равная
(равная  ) является бесконечно малой более высокого порядка, чем
) является бесконечно малой более высокого порядка, чем  , когда
, когда 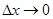 . Это часто используют при приближённых вычислениях.
. Это часто используют при приближённых вычислениях.
Очень часто при решении экономических задач возникает необходимость принять решение на основе исследования и анализа функций спроса, предложения, издержек, прибыли и т.д. При этом удобно пользоваться дифференциальным исчислением.
1. Возрастание/убывание функции
Если дифференцируемая функция y=f(х), х  возрастает на интервале
возрастает на интервале 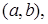 то f'(x0)
то f'(x0)  для любого х0
для любого х0 
Если дифференцируемая функция y=f(х), х  убывает на интервале
убывает на интервале 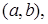 то f'(x0)
то f'(x0) 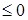 для любого х0
для любого х0 
2. Экстремумы функции
Точка х0 из области определения функции f(х) называется точкой минимума этой функции, если найдётся такая 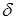 - окрестность
- окрестность  точки х0, что для всех
точки х0, что для всех  из этой окрестности выполняется неравенство f(х)> f(х0).
из этой окрестности выполняется неравенство f(х)> f(х0).
Точка х0 из области определения функции f(х) называется точкой максимума этой функции, если найдётся такая 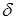 - окрестность
- окрестность  точки х0, что для всех
точки х0, что для всех  из этой окрестности выполняется неравенство f(х)< f(х0).
из этой окрестности выполняется неравенство f(х)< f(х0).
Точки минимума и максимума называются точками экстремума, а значения функции в этих точках называются экстремумами функции.
Необходимые условия существования экстремума даёт теорема Ферма:
Пусть функция y = f(x) определена на интервале (a, b) и в некоторой точке x0 этого интервала принимает наибольшее или наименьшее значение. Тогда возможны только два случая:
1) производная функции f'(x0) не существует;
2) f'(x0)=0.
Точки, в которых производная функции обращается в нуль или не существует, называются критическими точками (первого рода). Экстремум функции, если он существует, может быть только в критических точках. Однако не во всякой критической точке функция имеет экстремум. Поэтому, чтобы выяснить, в каких точках функция имеет экстремум, необходимо знать достаточные условия существования экстремума.
Первое достаточное условие экстремума. Пусть функция y=f(х) непрерывна в точке х0 и в некоторой её 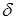 - окрестности имеет производную, кроме, быть может, самой точки х0. Тогда:
- окрестности имеет производную, кроме, быть может, самой точки х0. Тогда:
1) если производная f'(x) при переходе через точку х0 меняет знак с плюса на минус, то х0 является точкой максимума.
2) если производная f'(x) при переходе через точку х0 меняет знак с минуса на плюс, то х0 является точкой минимума.
3) если производная при переходе через точку х0 не меняет знак, то в точке х0 функция f(x) не имеет экстремума.
Второе достаточное условие экстремума. Если функция y=f(х) определена и дважды дифференцируема в некоторой окрестности точки х0, причём f'(x0)=0, а f''(x0)  0, то в точке х0 функция f(х) имеет максимум, еслиf''(x0)<0, и минимум, если f''(x0)>0.
0, то в точке х0 функция f(х) имеет максимум, еслиf''(x0)<0, и минимум, если f''(x0)>0.
3. Выпуклость графика функции
График функции y=f(х), х  (a,b) называется выпуклым вверх (вогнутым вниз) на интервале (a,b), если график расположен ниже (точнее не выше) любой своей касательной. Сама функция f(х) также называется выпуклой вверх (вогнутой вниз).
(a,b) называется выпуклым вверх (вогнутым вниз) на интервале (a,b), если график расположен ниже (точнее не выше) любой своей касательной. Сама функция f(х) также называется выпуклой вверх (вогнутой вниз).
График функции y=f(х), х  (a,b) называется выпуклым вниз (вогнутым вверх) на интервале (a,b), если график расположен выше (точнее не ниже) любой своей касательной. Сама функция f(х) также называется выпуклой вниз (вогнутой вверх).
(a,b) называется выпуклым вниз (вогнутым вверх) на интервале (a,b), если график расположен выше (точнее не ниже) любой своей касательной. Сама функция f(х) также называется выпуклой вниз (вогнутой вверх).
На интервале выпуклости вверх (вогнутости вниз) производная функции убывает. На интервале выпуклости вниз (вогнутости вверх) производная f'(x) возрастает.
Достаточное условие выпуклости графика функции. Если на интервале (a,b) дважды дифференцируемая функция y=f(х), х  (a,b) имеет отрицательную (положительную) производную второго порядка, то график функции является выпуклым вверх (вниз).
(a,b) имеет отрицательную (положительную) производную второго порядка, то график функции является выпуклым вверх (вниз).
Исследовать на выпуклость график функции y=f(х) означает найти те интервалы из области её определения, в которых вторая производная f''(x) сохраняет свой знак. Необходимо заметить, что f''(x) может менять свой знак лишь в точках, где f''(x)=0 или не существует. Такие точки принято называть критическими точками второго рода.
|
|
|
|
|
Дата добавления: 2015-05-10; Просмотров: 671; Нарушение авторских прав?; Мы поможем в написании вашей работы!