Использование производной при решении задач по экономической теории

Приложение производной в экономической теории

Проанализировав экономический смысл производной, нетрудно заметить, что многие законы теории производства и потребления, спроса и предложения оказываются прямыми следствиями математических теорем. Для примера рассмотрим экономическую интерпретацию теоремы Ферма.

Пусть q – выпуск продукции (в натуральных единицах); TR(q) – выручка от продаж; TC(q) – издержки производства, связанные с выпуском q единиц продукции. Тогда прибыль

Предположим, что выполняются следующие условия:

1) Функции TR(q), TC(q) определены на полуинтервале 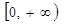и дифференцируемы при q>0.

2) Максимум прибыли достигается в некоторой точке q* 0.

В случае, когда максимум прибыли положителен 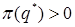, условие q* 0 естественным образом выполняется, поскольку (нет выпуска – нет выручки, нет выручки – нет прибыли).

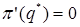Итак, условия 1), 2) выполнены. Тогда функция дифференцируема и имеет на интервале максимум в точке q* 0. По теореме Ферма, . Так как 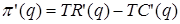, то в точке q=q* получаем равенство

TR'(q*)=TC'(q*) или MR=MC.

В экономической теории данное равенство иллюстрирует один из базовых законов теории производства, согласно которому фирма, максимизирующая свою прибыль, устанавливает объём производства таким образом, чтобы предельная выручка была равна предельным издержкам.

В случае, когда объём производства q не влияет на цену продукции p, имеем TR(q)=p*q, TR'(q)=p. РавенствоTR'(q*)=C'(q*) принимает вид p=TC'(q*).

Задача №1: Функция спроса имеет вид QD =100 – 20p, постоянные издержки TFC (total fixed costs)составляют 50 денежных единиц, а переменные издержки TVC (total variable costs) на производство единицы продукции – 2 денежные единицы. Найти объём выпуска, максимизирующий прибыль монополиста.

Решение: Прибыль есть выручка минус издержки:

П=TR – TC,

где TR=p*Q; TC=TFC+TVC.

Найдём цену единицы продукции:

20p=100 – Q p=5 – Q/20.

Тогда

П=(5 – Q/20)Q – (50 + 2Q)= – Q2 + 60Q - 1000 ® max

Найдём производную: П'(Q)= –2Q+60.

Приравняем производную к нулю: –2Q+60=0 Q=30.

При переходе через точку Q=30 функция П(Q) меняет свой знак с плюcа на минус, следовательно, эта точка является точкой максимума, и в ней функция прибыли достигает своего максимального значения. Таким образом, объём выпуска, максимизирующий прибыль, равен 30 единицам продукции.

Задача №2: Найти объём производства, при котором фирма, действующая на рынке совершенной конкуренции, будет получать максимальную прибыль, если p=15, TC(q)=q3 + 3q.

Решение: Прибыль фирмы, действующей на рынке совершенной конкуренции, максимизируется при равенстве предельной выручки и предельных издержек: MR=MC. Поскольку при совершенной конкуренции наблюдается равенство цены и предельной выручки: P=MR, то можно утверждать, что фирма максимизирует прибыль при P=MC.

Найдём предельные издержки: MC=TC'=3q2 + 3.

3q2 + 3=15;

3q2 =12 Þq=2.

Итак, мы выяснили, что при цене p=15 фирма предложит на продажу 2 единицы продукции.

Заключение

В результате проведенного исследования можно сделать следующие выводы:

1. Производная является важнейшим инструментом экономического анализа, позволяющим углубить геометрический и математический смысл экономических понятий, а также выразить ряд экономических законов с помощью математических формул.

2. При помощи производной можно значительно расширить круг рассматриваемых при решении задач функций.

3. Экономический смыслпроизводной состоит в следующем: производная выступает как скорость изменения некоторого экономического процесса с течением времени или относительно другого исследуемого фактора.

4. Наиболее актуально использование производной в предельном анализе, то есть при исследовании предельных величин (предельные издержки, предельная выручка, предельная производительность труда или других факторов производства и т. д.).

5. Производная находит широкое приложение в экономической теории. Многие, в том числе базовые, законы теории производства и потребления, спроса и предложения оказываются прямыми следствиями математических теорем (например, представляет интерес экономическая интерпретация теоремы Ферма, выпуклости функции и т. д.).

6. Знание производной позволяет решать многочисленные задачи по экономической теории.

Работу Выполнила Студентка группы №179

Дата добавления: 2015-05-10