Теорема умножения вероятностей

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, т.е.

(10) 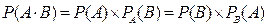для двух зависимых событий;

Для нескольких попарно зависимых событий А₁,А₂,…А_n:

(11)

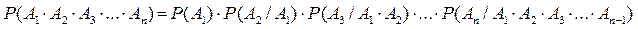
Для независимых событий теорема умножения вероятностей согласно (9) представлена формулой

(12) .

Пример:

В ящике имеется 10 электрических лампочек из которых 3 неисправны. На удачу одну за другой вынимают 2 лампочки.

А) какова вероятность, что обе исправны.

Б) какова вероятность, что обе неисправны.

В) какова вероятность, что одна из двух исправна.

Г) какова вероятность, что хотя бы одна исправна.

Решение: Обозначим события М-1^я-исправна; К-2^я-исправна

События М и К зависимые (т.е. вероятность события К меняется от того, произошло событие М или нет)

А)

Б)

В) "первая хорошая, вторая плохая или первая плохая, вторая хорошая"

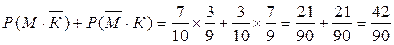
Г) " хотя бы одна исправна, т.е. одна или больше (≥ 1), первая исправна или вторая исправна

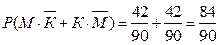
Замечание: Если вопрос задачи звучит как "хотя бы", то часто удобнее перейти к противоположному событию, т.е. "хотя бы одна исправная = 1 – Р (обе неисправны)"

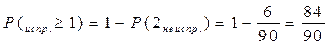
Пример:

Бросаем 2 монеты. Событие А – 2 герба, событие В – 2 решки, событие С – 1 герб и 1 решка. Являются ли равновозможными события? Результаты для каждой из монет независимы.

Решение:

А)

Б)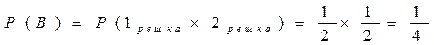

В) "герб и решка или решка и герб"

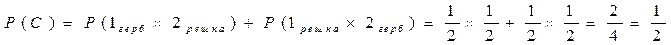
Формула полной вероятности и формула Байеса.

Пример:

Однотипная продукция выпускается 3-мя цехами, производительности которых относятся как 1:3:2. Вероятность брака в каждом цехе составляет соответственно 1, 2 и 3%. Все изделия хранятся на одном складе. Наудачу одно изделие выбирается на складе. Какова вероятность, что оно браковано.

Решение:

I – A₁ составляют полную группу

II – A₂

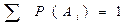
III – A₃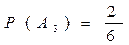

E – бракованное изделие

Пусть событие Е может произойти с любым из событий A₁, A₂, и т.д., образующих полную группу. Тогда полная вероятность события Е определяется формулой:

(12)

Пусть в условиях предыдущего примера известно, что наудачу взятое изделие оказалось бракованным.

А) какова вероятность, что оно было сделано в первом цеху.

Б) если известно, что изделие браковано, в каком цеху вероятнее всего было сделано.

Ответ на поставленный вопрос (переоценка гипотез при дополнении информации) дают формулы Байеса.

(13)

Доказательство:

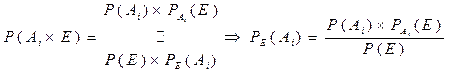
Выражая неизвестную величину через известные, получаем формулу 13, что и требовалось доказать.

С помощью формулы 13 отвечаем на вопрос задачи.

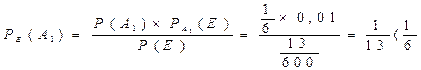
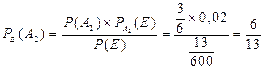
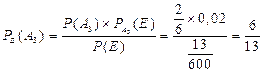
Значит, вероятнее всего бракованное изделие будет сделано впервом или втором цеху.

Дата добавления: 2015-05-26