Задачі для самостійного вирішення. Задача 6. Вентилятор обертається з частотою n = 900 об/хв

Задача 6. Вентилятор обертається з частотою n = 900 об/хв. Після виключення вентилятор, обертаючись рівноуповільнено, зробив до зупинки N = 75 обертів. Який час t пройшов з моменту виключення вентилятора до повної його зупинки? (Відповідь: t = 10 с).

Задача 7. Камінь, кинутий горизонтально, через час t =0,5 с після початку руху мав швидкість v, в 1,5 рази більше швидкості v_x у момент кидання. З якою швидкістю v_x кинутий камінь? (Відповідь: v_x = 4,4 м/с)

Задача 8. Дві матеріальні точки рухаються згідно рівнянням: x ₁= A ₁ t + B₁t²+ C₁t³ и x ₂= A ₂ t + B ₂ t ²+ C ₂ t ³, где A ₁=4 м/с, B ₁=8м/с, С ₁=-16 м/с, А ₂=2м/с, В ₂=-4 м/с², C ₂=1 м/с³. В який момент часу t прискорення цих крапок будуть однакові? Знайти швидкості v ₁ і v ₂ точок у цей момент. (Відповідь: t =0,235 с, v ₁ = 5,1 м/с, v ₂ = 0,29 м/с.)

Задача 9. Рівняння руху матеріальної точки уздовж осі х має вид х = At + Bt ² + Ct ³, де A = 2 м/с, B = -3 м/с², C = 4 м/с³. Знайти залежність швидкості v і прискорення точки від часу t; координату х, швидкість v і прискорення точки через t =2 з після початку руху. (Відповідь: х =24 м, v = 38 м/с, a =42 м/с ².)

Задача 10. Рух точки по прямой заданий рівнянням х = At + Bt ², де A =2 м/с, B = -0,5 м/с². Визначити середню путню швидкість < v > рухи точки в інтервалі часу від t ₁ =1 с до t ₂=3 с. (Відповідь: < v > = 0,5 м/с.)

Задача 11 Точка рухається по прямой згідно рівнянню х = At + Bt ³, де A = 6 м/с, B = -0,125 м/с³. Визначити середню путню швидкість < v > точки в інтервалі часу від t ₁ =2 с до t ₂ = 6 с. (Відповідь:< v >=3 м/с.).

Задача 12. Точка рухається по колу радіусом R = 4 м. Закон її руху виражається рівнянням ξ = A + Bt ², где A = 8 м, B = -2 м/с². Знайти момент часу t, коли нормальне прискорення точки a_n =9 м/с², а також швидкість v, тангенціальне прискорення a_τ і повне прискорення a _полн точки у цей момент. (Відповідь: t = 1,5 с, v = -6 м/с, a_τ = -4 м/с², a _полн = 9,84 м/с².)

Задача 13. Точка рухається по колу радіусу R = 10 см з постійним тангенціальним прискоренням a_τ. Знайти a_τ, якщо відомо, що до кінця п'ятого обороту після початку руху швидкість точки стала рівна v = 79,2 см/с. (Відповідь: a_τ = 0,1 м/с².)

Задача 14. В першому наближенні можна вважати, що електрон в атомі водню рухається по круговій орбіті з лінійною швидкістю v. Знайти кутову швидкість w обертання електрона навкруги ядра і його нормальне прискорення a_n. Прийняти радіус орбіти електрона рівним R = 0,5⋅10^{-10 мі лінійну швидкість електрона на цій орбіті v = 2,2⋅106} м/с.

(Відповідь: ω = 4,4⋅10¹⁶ рад/c, a _n=9,7⋅10²² м/с².)

Задача 15. З висоти h = 2 м вниз під кутом a = 30⁰ до вертикалі кинутий м'яч з початковою швидкістю v ₀ = 8,7 м/с. Знайти відстань S між двома послідовними ударами м'яча об землю. (Відповідь: S = 8,7 м.)

Тема 2. Динаміка матеріальної точки. Закон збереження імпульсу

Приклади рішення задач

Задача 1. На горизонтальній площині знаходяться зв'язані невагомою і нерозтяжною ниткою двоє тіла, маси яких m ₁ і m ₂. До тіла масою m ₂ прикладена сила F, направлена під кутом a до горизонту. Коефіцієнт тертя між вантажами і площиною рівний f. Визначити натягнення нитки і прискорення тел.

Рішення

На тіло масою m ₁ діють: сила тяжіння m ₁ g, сила реакції опори N ₁, сила натягнення нитки T ₁, сила тертя F т₁. На тіло масою m ₂ діють: сила тяжіння m ₂ g, сила реакції опори N ₂, сила натягнення нитки T ₂, сила тертя F т₂ і сила F. Направимо вісь х системи координат уздовж площини, а вісь у - перпендикулярно площини, як показано на малюнку.

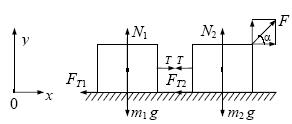
Оскільки по умові задачі нитка нерастяжима і невагома, то T ₁ = T ₂ = T і прискорення обох тіл однакові. Рівняння руху в проекціях на координатні осі можуть бути записані таким чином:

m ₁ a = T - F _т1,

m ₂ a = Fcos α - T - F _т2,

0 = N ₁ - m ₁ g,

0 = N ₂ - m ₂ g + Fsin α.

Оскільки коефіцієнт тертя f відомий, то отримаємо:

F _т1 = fN ₁ , F _т2 = fN ₂ .

Підставляємо отримані вирази в рівняння руху, маємо:

m ₁ a = T - fN ₁,

m ₂ a = Fcos α - T - fN ₂ ,

N ₁ = m ₁g,

N ₂ = m ₂ g - Fsin α.

Вирішуючи цю систему рівнянь, отримаємо відповідь до задачі:

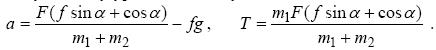
Задача 2. Потяг масою m = 500 т, рухаючись рівноуповільнено, протягом часу t = 1 хв. зменшує свою швидкість від v ₁ = 40 км/година до v ₂ = 28 км/година. Знайти силу гальмування F.

Рішення

Оскільки прискорення тіла постійно, воно може бути знайдено із співвідношення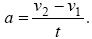

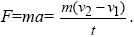
Підставляючи чисельні значення, отримаємо F = 27,8 кН.

Відповідь: F = 27,8 кН.

Задача 3. Горизонтально розташований диск обертається навкруги вертикальної осі, роблячи n = 25 оборотів за хвилину. На якій відстані R від осі обертання диска може утриматися тіло, що знаходиться на ньому, якщо коефіцієнт тертя f = 0,2?

Рішення

Єдиною силою, діючою на тіло в горизонтальному напрямі і перешкоджаючій його зісковзуванню з диска, є сила тертя F. У вертикальному напрямі на тіло діють дві рівні по величині але протилежно направлені сили - сила тяжіння mg і сила реакції опори N. Оскільки диск рівномірно обертається, повне прискорення тіла рівно нормальному прискоренню a_n = ω² R, де w - кутова швидкість обертання тіла. Рівняння руху тіла у момент початку зісковзування може бути записано таким чином: m ω² R = F. Ураховуючи, що F = fmg, і ω = 2π n, одержуємо

.

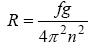Підставляючи чисельні значення, знаходимо R = 0,29 м.

Відповідь: R = 0,29 м.

Задача 4. На невагомій і нерозтяжній нитці, перекинутій через нерухомий блок, підвішені два вантажі масами m ₁ = 3 кг і m ₂ = 5 кг як показано на малюнку. Визначити прискорення вантажів і сили натягнення ниток. Масою блоку і силою тертя в блоці нехтувати.

Рішення

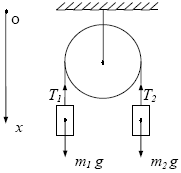Оскільки нитка нерозтяжна і невагома, а масою блоку і силою тертя можна нехтувати, то обидва вантажі будуть рухатися з рівними по модулю прискореннями, і модулі сил натягнення нитки T ₁ і T ₂ по обидві сторони блоку будуть рівні між собою. Виберемо позитивний напрям осі х зверху вниз (див. малюнок). На кожний з вантажів діють дві сили: сила тяжіння і сила натягнення нитки. Рівняння руху вантажів можуть бути записані таким чином:

m₂a = m₂g - T₁, - m₁a = m₁g - T₂ , T₁ = T₂ .

Вирішуючи отриману систему рівнянь, знаходимо:

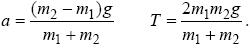
Підставляючи чисельні значення, отримаємо a = 2,45 м/с², T = 36,75 H.

Відповідь: a = 2,45 м/с², T =36,75 H.

Задача 5. Снаряд розривається у верхній точці траєкторії на два рівні уламки. Перший уламок впав на відстані s від місця розриву (по горизонталі), другий уламок впав вертикально вниз. Визначити швидкість снаряда у момент розриву, якщо відомо, що вибух відбувся на висоті H, а уламок, що впав по вертикалі, падав час T.

Рішення

Рух осколків відбувається під дією тільки сили тяжіння. Направимо вісь х по горизонталі, а вісь у по вертикалі (див. малюнок).

За початок відліку часу приймемо момент вибуху. Координати осколків в початковий момент часу будуть рівні:

x ₁₀=0, x ₂₀=0, y ₁₀= H, y ₂₀= H.

Проекція швидкості другого уламка на вісь х рівна v _{20 x} = 0. Закон руху осколків може бути записаний таким чином:

x₁ = v_10x t, y₁ = H + v_10y t - gt²/2,

x₂ = 0, y₂ = H - v_20y t - gt²/2.

У момент падіння на землю y₁ = y₂ = 0, x₁ = s, тобто можна записати:

s = v_10x T₁, (1)

0 = H + v_10y T₁ - gT²/ 2 (2)

0 = H - v_20yT - gT²/2 (3)

Тут час польоту першого уламка позначений T ₁ .

У верхній точці траєкторії швидкість снаряда направлена по горизонталі. Отже, на підставі закону збереження імпульсу, вертикальні складові швидкостей осколків відразу після вибуху рівні по величині і протилежні по напряму, тобто:

v_10y = -v_20y. (4)

Для горизонтального направлення із закону збереження імпульсу слід: mv = (m/2)v_10х, де m - маса снаряда до вибуху, v - швидкість снаряда. Скорочуючи на m, одержуємо v=v10х/2. Використовуючи вираз (1), одержуємо: 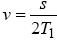(5)

З рівняння (3) знаходимо, що

.

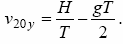Підставляючи отриманий вираз в (2), одержуємо квадратне рівняння для визначення T1 - часу польоту першого уламка:

gTT₁² - (2H-gT²)T₁ - 2HT = 0.

Вирішуючи це рівняння і відкидаючи негативний корінь, одержуємо:

.

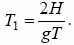Підставивши отримане значення для Т ₁ в (5), знаходимо шукану швидкість снаряда.

Дата добавления: 2015-05-26