Задачі для самостійного вирішення

Задача 6. Куля, що рухається із швидкістю v1=10 м/с, пружно стикається з кулею, що покоїться і має в n = 5 раз велику масу, і відлітає в напрямі, перпендикулярному напряму його первинного руху. Визначити швидкості u ₁ і u ₂ куль після удару. (Відповідь: u ₁ = 8,16 м/с, u ₂ = 2,58 м/с.)

Задача 7. З пружинного пістолета вистрілили кулею, маса якої m = 5 г. Жорсткість пружини k = 1,25 кН/м. Пружина була стиснута на Δ x = 8 см. Визначити швидкість кулі v при вильоті її з пістолета. (Відповідь: v =40 м/с).

Задача 8. Куля масою m = 1,8 кг стикається з кулею більшої маси M, що покоїться. В результаті прямого пружного удару куля втратила частку η = 0,36 своїй кінетичній енергії T ₁. Визначити масу більшої кулі. (Відповідь: M = 16,2 кг.)

Задача 9. Ковзаняр, стоячи на льоду, кинув вперед гирю масою m = 5кг і унаслідок віддачі покотився назад із швидкістю v = 1 м/с. Маса ковзаняра M = 60 кг. Визначити роботу А, виконану ковзанярем при киданні гирі. (Відповідь: A = 390 Дж.)

Задача 10. Тіло масою m = 0,1 кг падає з висоти H = 0,1 м на горизонтальну пластинку масою M = 0,2 кг, лежачу на верхньому кінці вертикально розташованої пружини, коефіцієнт жорсткості якої k = 20 Н/м. В результаті абсолютно непружного зіткнення пластинка опустилася на відстань h від свого первинного положення. Стиснення пружини відбувається в області пружної деформації. Визначити h. (Відповідь: h=0,13 м.)

Задача 11. Обчислити роботу, виконану на шляху S = 12 м рівномірно зростаючою силою, якщо на початку шляху сила була рівна F ₁ = 10 Н, а в кінці шляху - F ₂ = 46 Н. (Відповідь: A = 336 Дж.)

Задача 12. Сталева кулька масою m = 20 г, падаючи з висоти h = 1 м на сталеву плиту, відскакує від неї на висоту Н = 81 см. Знайти імпульс р, отриманий плитою за час удару, і кількість теплоти Q, що виділилася при ударі. (Відповідь: р = 0,17 кгм/с, Q = 37,2 мДж.)

Задача 13. Знайти роботу А, яку треба здійснити, щоб збільшити швидкість руху тіла масою m = 1 кг від v ₁ = 2 м/с до v ₂ = 6 м/с на шляху завдовжки S = 10 м. На всьому шляху діє сила тертя F = 2 Н. (Відповідь: А = 36 Дж.)

Задача 14. З гори заввишки h = 2 м і завдовжки підстави b = 5 м з'їжджають санки, які потім зупиняються, пройшовши по горизонталі відстань L = 35 м від підстави гори. Знайти коефіцієнт тертя f. (Відповідь: f = 0,05.)

Задача 15. Локомотив масою M = 8,6 т починає рухатися із станції так, що його швидкість міняється згідно із законом, 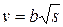де b = 0,22 м/с, s - пройдений шлях, узятий в метрах. Знайти сумарну роботу А всіх сил, діючих на локомотив за перші t = 5 хвилин після початку руху. (Відповідь: A = 226 кДж).

Тема 4. Динаміка твердого тіла. Основне рівняння динаміки обертального руху.

Приклади рішення задач.

Задача 1. Вал у вигляді суцільного циліндра масою m ₁ = 10 кг насаджений на горизонтальну вісь. На циліндр намотаний шнур, до вільного кінця якого підвішена гиря масою m ₂ = 2 кг. З яким прискоренням а буде опускатися гиря, якщо її надати самій собі?

Рішення

Лінійне прискорення гирі рівно тангенціальному прискоренню точок валу, що лежать на його циліндровій поверхні, і пов'язано з кутовим прискоренням валу співвідношенням:

a = ε r (1)

де r -радиус валу.

Кутове прискорення валу виражається основним рівнянням динаміки тіла, що обертається:

ε = M/J (2)

де M - обертаючий момент, діючий на вал; J -момент інерції валу щодо осі обертання. Розглядаємо вал як однорідний циліндр. Тоді його момент інерції щодо геометричної осі рівний:

J = m ₁r² /2. (3)

Обертаючий момент M, діючий на вал, рівний добутку сили натягнення T шнура на радіус валу:

M = Tr. (4)

Силу натягнення шнура знайдемо з наступних міркувань. На гирю діють дві сили: сила тяжіння m ₂ g, направлена вниз, і сила натягнення T шнура, направлена вгору. Рівнодіюча цих сил викликає рівноприскорений рух гирі. По другому закону Ньютона:

m ₂ g - T = m ₂ a. (5)

Підставивши (3-5) в (2), одержуємо кутове прискорення е валу:

ε = 2 m ₂(g-a)/ m ₁ r ². (6)

Для визначення лінійного прискорення гирі підставимо останній вираз у формулу (1) і отримаємо: а = 2 m 2 g /(m ₁+2 m ₂) = 2,80 м /с² .

Відповідь: а = 2,80 м/с².

Задача 2. До обода однорідного диска радіусом R = 0,5 м і масою m = 50 кг прикладена дотична сила F = 200 Н. При обертанні на диск діє момент сил тертя M _тр= 25 Н×м. Знайти кутове прискорення диска e і момент часу t після початку руху, коли диск буде мати частоту обертання n = 10 об/с.

Рішення

Згідно основному рівнянню динаміки обертального руху:

J ε = FR - M _тр (1)

де J = mR ²/2 - момент інерції диска. Результуючий момент сил, під дією якого обертається диск рівний: (FR-M _тр), оскільки момент сили F і момент сили тертя направлений протилежно.

З (1) знаходимо кутове прискорення:

ε = 2(FR-M _тр)/(mR ²) = 12 рад/с² . (2)

Оскільки кутове прискорення постійно, то шуканий час визначимо з рівняння:

t = ω/ε = 2π n /ε = 5,23 с (3)

де ω=2p n - кутова швидкість.

Відповідь: e = 12 рад/с², t=5,23 с.

Задача 3. Знайти момент інерції системи з трьох вантажів масою m = 1кг кожний, розміщених у вершинах невагомого рівностороннього трикутника із стороною a = 1 м, відносно осі, що перпендикуляра площини трикутника і проходе через третю частину одній з його сторін.

Рішення

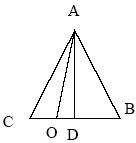Момент інерції системи буде рівний сумі моментів інерції окремих її частин. Розглянемо трикутник АВС (див. малюнок). З малюнка видно, що відстань двох вантажів від осі обертання буде рівна:

OC = r ₁ = a /3, OB = r ₂ = 2 a /3.

Для визначення відстані між віссю і третім вантажем розглянемо трикутник АОD. В цьому трикутнику OD = a /2 - a /3 = a /6, AD = a

і відстань від третього вантажу до осі:

OA = r ₃ = (a ²/36 + 3 a ²/4)^1/2 =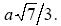

Момент інерції системи вантажів рівний

J = m r ₁² + m r ₂² + m r ₃² = 4/3 ma ².

Підставляючи чисельні значення, отримаємо відповідь: J = 1,3 кг×м².

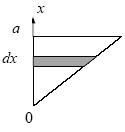Задача 4. Знайти момент інерції плоского рівнобедреного прямокутного трикутника із стороною a = 0,2 м і масою m = 1 кг відносно осі, співпадаючої з однією з його сторін.

Рішення

Направимо вісь х уздовж одного з катетів, за початок відліку приймемо вершину трикутника (див. малюнок). Розіб'ємо площу трикутника на нескінченно малі шари шириною dx, перпендикулярні осі обертання. Розглянемо один з таких шарів, розташований на відстані х від початку координат. Оскільки момент інерції тіла відносно якої-небудь осі рівний сумі моментів інерції його частин відносно цієї осі, то момент інерції трикутника буде рівний сумі моментів інерції виділених шарів. Кожний шар є стрижнем з довжиною, рівній х (оскільки кут при вершині трикутника рівний 45⁰, довжина кожного шару рівна відстані від шару до початку координат). Момент інерції стрижня завдовжки х відносно осі, що перпендикулярна до стрижня і проходе через його кінець, дорівнює

dJ =1/3⋅ x ² dm,

де dm - маса шару завдовжки х і шириною dx. Щоб знайти величину dm, потрібно площа шару помножити на масу одиниці площі. Оскільки площа трикутника рівна S = a ²/2, а площа шару рівна xdx, то маса шару виражається як:

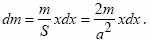
Момент інерції шару буде рівний

.

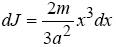Тоді для моменту інерції трикутника одержуємо вираз:

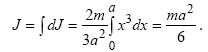
Підставляючи чисельні значення, знаходимо J = 0,0067 кг×м².

Відповідь: J = 0,0067 кг×м².

Задача 5. Знайти момент інерції J плоского кільця масою m = 1 кг щодо осі, перпендикулярної площини кільця і проходячій через точку, що лежить на зовнішньому краї кільця. Внутрішній радіус кільця рівний r = 10 см, зовнішній – R = 20 см.

Рішення

Згідно теоремі Штейнера, момент інерції кільця J відносно осі, перпендикулярної його площини і проходячій через точку на краю кільця, може бути обчислений таким чином:

J = J ₀ + ma ²,

де J ₀ - момент інерції відносно осі, що проходить через центр мас (центр кільця), - відстань між віссю і центром мас. В нашому випадку a = R. Для знаходження моменту інерції J ₀ візьмемо до уваги, що момент інерції будь-якого тіла рівний сумі моментів інерції його частин. Відповідно, момент інерції J ₁ суцільного диска радіусом R відносно його осі рівний сумі моменту інерції J ₂ суцільного диска радіусу r відносно цієї осі, і моменту інерції кільця J ₀ . Моменти інерції дисків рівні, відповідно: J ₁ = M ₁ R ²/2 і J ₂ = M ₂ r ²/2, де M ₁ і M ₂ - маси дисків. Тоді можна записати:

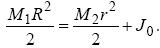
З останнього виразу одержуємо:

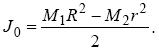
Якщо густина матеріалу кільця r, а його товщина d, то M₁ = rpd R ², M ₂ = rpdr² і маса кільця m= rpd(R ² - r ²), звідки

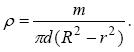
Підставляючи знайдені значення r, M ₁ і M ₂ у вираз для J ₀, одержуємо:

,

звідки випливає:

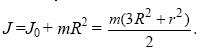
Підставляючи чисельні значення, остаточно знаходимо J = 0,065 кг×м².

Відповідь: J = 0,065 кг м².

Дата добавления: 2015-05-26