Задачі для самостійного вирішення. Задача 6. Однорідний стрижень завдовжки L = 1 м і масою m = 0,5 кг обертається у вертикальній площині навкруги горизонтальної осі

Задача 6. Однорідний стрижень завдовжки L = 1 м і масою m = 0,5 кг обертається у вертикальній площині навкруги горизонтальної осі, що проходить через середину стрижня. З яким кутовим прискоренням e обертається стрижень, якщо на нього діє момент сил M = 0,098 Н×м?

(Відповідь: e = 2.35 рад/с².)

Задача 7. Колесо, момент інерції якого J = 245 кг×м², обертається з частотою n =20 об/с. Через час t = 1 хв. після того, як на колесо перестав діяти момент сил M, воно зупинилося. Знайти момент сил тертя M ₁ і число оборотів N, яке зробило колесо до повної зупинки після припинення дії сил. Колесо вважати однорідним диском. (Відповідь: M ₁ = 513 Н×м, N =600об.)

Задача 8. Дві гирі з масами m ₁ = 2 кг і m ₂ = 1 кг сполучено ниткою, перекинутою через блок масою m = 1кг. Знайти прискорення, з яким рухаються гирі, і сили натягнення T ₁ і T ₂ ниток, до яких підвішені гирі. Блок вважати однорідним диском. Тертям нехтувати. (Відповідь: a = 2,8 м/с², T 1 = 14 Н, T ₂ = 12,6 Н.)

Задача 9. На барабан радіусом R = 20 см, момент інерції якого J = 0,1 кг×м ², намотаний шнур, до кінця якого прив'язаний вантаж масою m = 0,5кг. До початку обертання барабана висота вантажу над підлогою була рівна h = 1 м. Через який час t вантаж опуститься до підлоги? Знайти кінетичну енергію Е_k вантажу у момент удару об підлогу і силу натягнення нитки T. Тертям нехтувати. (Відповідь: t = 1,1 с, Е_k = 0,81 Дж, T = 4,1 Н.)

Задача 10. Однорідний диск радіусом R = 0,2 м і масою m = 5 кг обертається навкруги осі, що проходить через його центр перпендикулярно до площини диска. Залежність кутової швидкості w обертання диска від часу t дається рівнянням w = A + Bt, де B = 8 рад/с². Знайти дотичну силу F, прикладену до обода диска. Тертям нехтувати. (Відповідь: F = 4 Н.)

Задача 11. Дві маленькі кульки масою m = 10 г кожна скріпляють тонким невагомим стрижнем завдовжки L = 20 см. Визначити момент інерції J системи відносно осі, що перпендикулярна до стрижня і проходе через центр мас системи.

(Відповідь: J = 0,0002 кг×м².)

Задача 12. Визначити момент інерції J тонкого однорідного стрижня завдовжки L = 30 см і масою m = 100 г відносно осі, що перпендикулярна до стрижня і проходе через: 1) його кінець; 2) його середину; 3) точку, віддалену від кінця стрижня на 1/3 його довжини.

(Відповідь: J ₁=0,003 кг×м ², J ₂= 0,00075 кг×м², J ₃ = 0,001 кг×м ².)

Задача 13. Знайти момент інерції J плоскої однорідної прямокутної пластини масою m =800 г відносно осі, співпадаючої з однією з її сторін, якщо довжина іншої сторони дорівнює L = 40 см. (Відповідь: J = 0,0427 кг×м²).

Задача 14. Визначити момент інерції J тонкого однорідного диска масою m = 100 г і радіусом R = 30 см відносно осі, що перпендикулярна до диска і проходе через середину його радіусу. (Відповідь: J = 0,00675кг×м²).

Задача 15. Визначити момент інерції J кільця масою m = 50 г і радіусом R = 10 см відносно осі, що лежить в площині кільця і дотичній до нього. (Відповідь: J = 0,00075кг×м²).

Тема 5. Закон збереження моменту імпульсу. Енергія обертального руху.

Приклади рішення задач.

Задача 1. Платформа у вигляді диска радіусом R = 1,5 м і масою M = 180 кг обертається за інерцією біля вертикальної осі з частотою n = 10 об/хв. В центрі платформи стоїть людина масою m = 60 кг. Яку лінійну швидкість відносно підлоги приміщення буде мати людина, якщо він відійде від центру платформи на відстань, рівну половині радіусу платформи?

Рішення

Використовуючи закон збереження моменту імпульсу, можна записати:

(J ₁+ J ₂)ω₁ = (J ₁+ J)ω₂ , (1)

де J ₁ - момент інерції платформи; J ₂ - момент інерції людини, що стоїть в центрі платформи; w₁ - кутова швидкість платформи з людиною, що стоїть в центрі; J - момент інерції людини, що знаходиться від краю платформи на відстані R /2; w₂ - кутова швидкість платформи з людиною, що знаходиться від краю платформи на відстані R /2. Лінійна швидкість людини, віддаленої від краю платформи на R /2, пов'язана з кутовою швидкістю співвідношенням:

v = ω₂ R /2. (2)

Визначивши ω₂ з рівняння (1) і підставивши отриманий вираз у формулу (2), будемо мати:

v = [(J ₁+ J ₂)ω₁ R ]/(J ₁+ J). (3)

Момент інерції платформи розраховуємо як для диска. Отже, J ₁= МR ²/2. Момент інерції людини розраховуємо як для матеріальної точки. Тому: J ₂= 0, J = mR ²/4. Кутова швидкість платформи до переходу людини рівна w₁ =2π n. Підставивши J ₁, J ₂, J і w₁ в співвідношення (3), отримаємо:

v = 2π nMR /(2M+m) = 0,67 м/с.

Відповідь; v = 0,67 м/с.

Задача 2. Стрижень завдовжки L = 1,5 м і масою M = 10 кг може обертатися навкруги нерухомої осі, що проходить через верхній кінець стрижня. В нижній край стрижня ударяє куля масою m = 10 г, що летить в горизонтальному напрямі із швидкістю v = 500 м/с, і застряє в стрижні. На який кут a відхилиться стрижень після удару?

Рішення

Удар кулі слід розглядати як непружний: після удару куля і відповідна точка стрижня будуть рухатися з однаковими швидкостями. Спочатку куля, ударившись об стрижень, за нікчемо малий проміжок часу приводить його в рух з кутовою швидкістю w і вітдає йому кінетичну енергію:

T = J ω²/2, (1)

де J - момент інерції стрижня щодо осі обертання. Потім стрижень повертається на шуканий кут?, причому центр мас стрижня підіймається на висоту h = (L /2)(1-cosϕ). У відхиленому положенні стрижень буде володіти потенційною енергією:

П = Mg (L /2)(1 - cosϕ). (2)

Потенційна енергія отримана за рахунок кінетичної енергії і рівна їй за законом збереження енергії. Прирівнявши праві частини рівності (1) і (2), і підставивши вираз для моменту інерції стрижня щодо осі, що проходить через край стрижня і перпендикулярній йому (J = ML ²/3), отримаємо:

cosϕ = 1 - L ω²/(3 g), (3)

Застосувавши закон збереження моменту імпульсу, можемо написати:

mvL = (J + mL ²)ω. (4)

Підставивши щ з (4) в (3), отримаємо:

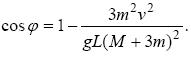
Підставляючи числові значення, знаходимо cosa = 0,95, звідки a» 18°.

(Відповідь: a» 18°.)

Задача 3. Дві кулі різного діаметра починають котитися з однаковою швидкістю v = 100 см/с вгору по похилій площині під кутом a = 30⁰ до горизонту. Менша куля зроблена з алюмінію, інший із сталі. Який шлях пройде кожну з куль до зупинки?

Рішення

Хай маса одного з куль рівна m, а радіус його R. Енергія кулі, що рухається, рівна W = mv ²/2+ J ω²/2, де J = 2/5 mR ²-момент інерції кулі, w - кутова швидкість обертання. Оскільки куля рухається без прослизання, то w = v / R. Висоту підйому кулі по похилій площині h знаходимо із закону збереження енергії:

mv ²/2 + J ω²/2 = mgh.

Підставляючи в цей вираз значення моменту інерції кулі і кутової швидкості, одержуємо mv ²/2 + mv ²/5 = mgh, звідки слідує h = 7v²/(10 g). Шлях, пройдений кулею уздовж похилої площини до зупинки, зв'язаний у висотою підйому співвідношенням:

З отриманого виразу видно, що висота підйому і, відповідно, шлях, пройдений кулею до зупинки, не залежить від маси і діаметра кулі, а визначається лише значенням його швидкості. Таким чином, для куль, виготовлених з різних матеріалів, пройдений шлях буде однаковий. Підставляючи чисельні значення, отримаємо S = 14 см.

Відповідь: S = 14 см.

Задача 4. Свинцевий диск, що обертається з частотою n = 100 об/с, радіусом R = 10 см і завтовшки h =1 см опустили в судину з водою об'ємом V = 10 літрів. Знайти зміну температури води D T в судині унаслідок гальмування диска. Початкові значення температури диска і води однакові, густина свинцю r_с = 11300 кг/м³, густина води r_в = 1000 кг/м³, питомі теплоємності свинцю і води рівні С _с =130 Дж/(кг×К), С _в = 4,2 кДж/(кг×K).

Рішення

Зміну температури води в судині знайдемо виходячи з рівняння теплового балансу:

W = m _с C _с Δ T + m _в С _в Δ T

де W - енергія диска, що обертається, m _с і m _в - маси свинцю і води.

З цього рівняння одержуємо:

D T = W /(m _с С _с + m _в С _в).

Енергію W знаходимо із співвідношення W = J ω²/2, де J - момент інерції диска, w - його кутова швидкість. Для диска J = m _с R ²/2. Кутова швидкість пов'язана з кількістю оборотів в одиницю часу як w =2p n. Маса тіла рівна добутку його густини на об'єм:

m _с = ρ_сπ R ² h, m _в=ρ_в V.

Підставляючи знайдені значення, одержуємо розрахункову формулу:

Підставляючи сюди чисельні значення параметрів, знайдемо D T = 0,08 К.

Відповідь: D T = 0,08 К.

Задача 5. Два горизонтальні диски вільно обертаються навкруги вертикальної осі, що проходить через їх центри. Моменти інерції дисків щодо цієї осі рівні J ₁= 0,25 кг⋅м² і J 2=0,40кг⋅м², а кутові швидкості w₁ = 6 рад/с і w₂ = 3 рад/с. Після падіння верхнього диска на нижній, обидва диски, завдяки тертю між ними, почали через деякий час обертатися з однаковою кутовою швидкістю. Знайти роботу сили тертя.

Рішення

Робота сил тертя буде рівна різниці кінетичної енергії двох дисків, що обертаються, до їх зіткнення і кінетичної енергії системи, що утворилася, після того, як обидва диски почали обертатися разом. Знайдемо енергію першого W ₁ і другого W ₂ дисків: W ₁ = J ₁ω₁²/2, W = J ₂ω₂²/2. Момент інерції системи, що утворилася, рівний J = J ₁ + J ₂, а кутова швидкість обертання рівна w. Тоді енергія системи буде рівна W = J w²/2. Робота сил тертя знаходиться із співвідношення:

A = W ₁ + W ₂ – W (1)

Для знаходження кутової швидкості обертання системи дисків скористаємося законом збереження моменту імпульсу (з умови задачі витікає, що система є замкнутою, і, отже, момент імпульсу не змінюється). Маємо: J ₁w₁+ J ₂w₂ = (J ₁ + J ₂)w, звідки слід:

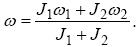
Підставляючи знайдені значення W, W ₁, W ₂ і щ в рівняння (1), отримаємо:

Підставивши сюди чисельні значення, знайдемо роботу A = 0,69 Дж.

Відповідь: A = 0,69 Дж.

Дата добавления: 2015-05-26