Задачі для самостійного вирішення. Задача 6. Людина масою m = 70 кг знаходиться на нерухомій платформі масою M = 30 кг

Задача 6. Людина масою m = 70 кг знаходиться на нерухомій платформі масою M = 30 кг. З якою кутовою швидкістю w буде обертатися платформа, якщо людина почне рухатися по колу радіусу r = 0,7 м навкруги осі обертання. Швидкість руху людини щодо платформи рівна v =1,2 м/с. Радіус платформи R = 1,5 м. Вважати платформу круглим однорідним диском, а людини точковою масою. (Відповідь: w = 0,75 рад/с.)

Задача 7. Хлопчик котить обруч по горизонтальній дорозі із швидкістю v = 2 м/с. На яку висоту H може вкотитися обруч на гору за рахунок своєї кінетичної енергії? (Відповідь: H = 0,4 м.)

Задача 8. Однорідний стрижень завдовжки L = 60 см підвішений на горизонтальній осі, що проходить через верхній кінець стрижня. Кулька, що летить перпендикулярно до осі стрижня, ударяє в його середину і пружно відскакує без втрати швидкості. Знайти швидкість v кульки, якщо стрижень відхилився на прямий кут. Маса стрижня в n =10 раз більше маси кульки: M = 10 m. (Відповідь: v = 14 м/с.)

Задача 9. Дві маленькі кульки масами m ₁ = 40 г і m ₂ = 120 г сполучені стрижнем завдовжки l = 20 см, маса якого нікчемо мала. Система обертається біля осі, що перпендикулярна до стрижня і проходе через центр інерції системи. Визначити імпульс р і момент кількості руху L системи. Частота обертання системи рівна n = 3 об/с. (Відповідь: р =0, L = 0,0226 кг×м²/с.)

Задача 10. Платформа у вигляді диска обертається за інерцією біля вертикальної осі з частотою n ₁ = 15 об/хв. На краю платформи стоїть людина. Коли людина перейшла в центр платформи, частота зросла до n ₂ = 25 об/хв. Маса людини m = 70 кг. Визначити масу M платформи. Момент інерції людини розраховувати як для матеріальної точки. (Відповідь: M =210 кг).

Задача 11. З похилої площини скачуються без ковзання суцільний і порожнистий циліндри. Знайти відношення швидкостей їх центрів тяжіння: 1) після закінчення часу t від початку руху; 2) в результаті скачування з висоти H. [Відповідь: 1) v ₁/ v ₂ = 4/3; 2) v ₁/ v ₂ = ].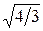

Задача 12. Знайти лінійні прискорення a ₁, a ₂ і a ₃ центрів кулі, диска і обруча, що скачується без ковзання з похилої площини. кут нахилу площини a = 30°, початкова швидкість всіх тіл v = 0. Порівняти знайдені прискорення з прискоренням тіла, що зісковзує з похилої площини за відсутності тертя. (Відповідь: a ₁ = 3,50 м/с², a ₂ = 3,27 м/с², a ₃ = 2,44 м/с², a = 4,9 м/с²).

Задача 13. Вертикальний стовп заввишки h = 5 м підпилюється у підстави і падає на землю. Визначити лінійну швидкість v його верхнього кінця у момент удару об землю. (Відповідь: v = 12 м/с).

Задача 14. Куля масою m = 10 г летить із швидкістю v = 800 м/с, обертаючись біля подовжньої осі з частотою n = 3000 об/с. Приймаючи кулю за циліндр діаметром d = 8 мм, визначити повну кінетичну енергію T кулі. (Відповідь: T = 3,21 кДж.)

Задача 15. До обода диска масою m = 5 кг прикладена дотична сила F = 19,6 Н. Яку кінетичну енергію E буде мати диск через час t = 5 с після початку дії сили? (Відповідь: E =1,92 кДж.)

Тема 6. Механічні коливання.

Приклади рішення задач.

Задача 1. Однорідний стрижень завдовжки L = 0,5 м здійснює малі коливання у вертикальній площині біля горизонтальної осі, що проходить через його верхній кінець. Найти період коливань Т стрижня.

Рішення.

Для періоду коливань T фізичного маятника маємо вираз:

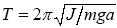
Відповідь: T=1,16 с.

Задача 2. Обчислити період малих коливань поплавця - вертикально розташованого циліндра, якому повідомили невеликий поштовх у вертикальному напрямі. Маса поплавця m =50 г, його радіус R =3,2 мм, густина рідини r = 1,00 г/см³. В'язкість рідини вважати рівною нулю.

Рішення

На поплавець діють дві сили: сила тяжіння і сила, що виштовхує F_{a .} В положенні рівноваги ці сили рівні по величині і протилежні по напряму. Якщо тіло змістити вниз від положення рівноваги у вертикальному напрямі на величину х, то виникне, згідно закону Архімеда, сила, направлена убік, протилежний зсуву, і рівна F _A= -ρ gV, де V - об'їм рідини, витиснений тілом при його відхиленні від положення рівноваги, m = r V - маса витисненої рідини.

Об'їм V = ρ R 2 x, і тому F _A= -ρ g π R ² x. Знак “-” указує, що напрям дії сили протилежно напряму зсуву х. Тоді рівняння руху поплавця можна записати таким чином:

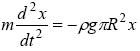чи

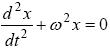
Порівнюючи отриманий вираз з диференціальним рівнянням незгасаючих коливань

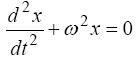
де ω - кругова частота, одержимо

.

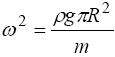Так як T = 2π/ω, то період коливань дорівнює:

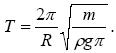
Подставляя численные значения, находим, что T = 2,5 с.

Відповідь: T=2,5 с.

Задача 3. Амплітуда коливань математичного маятника завдовжки L = 1 м за час t =10хв. зменшилася в n = 2 рази. Визначити логарифмічний декремент коливань q.

Рішення

Залежність амплітуди затухаючих коливань від часу має вигляд A (t)= A ₀exp(-δ t), де A₀ - амплітуда коливань у момент часу t = 0, δ - коефіцієнт загасання. Логарифмічний декремент коливань q визначається таким чином:

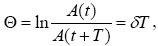
де A (t) і A (t+T) - амплітуди двох послідовних коливань, віддалених за часом один від одного на час T, рівне періоду коливань.

По умові задачі A (t)= A ₀/ N, звідки одержуємо: exp(-δ t)=1/ N і d = (ln N)/ t / Період коливань математичного маятника рівний:

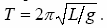
Підставляючи величини T і d, знаходимо логарифмічний декремент коливань:

.

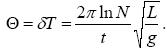Використовуючи чисельні значення, одержуємо q = 0,00232.

Відповідь: q = 0,00232.

Задача 4. Визначити максимальні значення швидкості і прискорення точки, що здійснює гармонійні коливання з амплітудою A = 3 см і кутовою частотою w = π/2 c^-1.

Рішення

Рівняння гармонійних коливань має вигляд: x = A cos(ω t + j), де j - початкова фаза коливань. Швидкість руху точки v і її прискорення а знайдемо, обчисливши похідні:

v = dx / dt = - A ω sin(ω t + ϕ) і a = dv / dt = - A ω²cos(ω t +ϕ). Максимальні значення функцій sin x і cos x рівні 1. Відповідно, максимальні значення модулів швидкості і прискорення точки будуть рівні: v _max= A ω, a _max = A ω². Підставляючи чисельні значення, отримаємо v _max = 4,71см/с, a _max = 7,40 см/с².

Відповідь: v _max = 4,71см/с, a _max = 7,40 см/с².

Задача 5. Складаються двоє коливання однакового напряму, описуваного рівняннями x ₁= A ₁cosω t и x ₂= A ₂ cos(ω t +π/3), де A ₁ = 4 см, A ₂ =2 см. Знайти амплітуду результуючого коливання.

Рішення

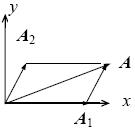Для вирішення задачі зручніше всього використовувати метод векторних діаграм. Діаграма складання коливань показана на малюнку. Оскільки початкова фаза першого коливання рівна нулю, то вектор, відповідний цьому коливанню, направлений уздовж осі абсцис. Вектор, відповідний другому коливанню, складає з віссю х кут p/3, рівний початковій фазі другого коливання. Амплітуду результуючого коливання знаходимо з трикутника AA₁O по теоремі косинусів:

A ² = A ₁² + A ₂² -2 A ₁ A ₂cos(π-π/3).

Підставляючи чисельні значення, отримаємо A = 5,3 см.

Відповідь: A = 5,3 см.

Дата добавления: 2015-05-26