Планирование экстремальных экспериментов. Планы первого порядка

Методика определения ограничений с помощью эксперимента

1. Разделить параметры объекта исследования, на факторы x_j (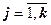) и отклики y_i (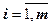) (k+m=n – общему числу параметров объекта).

2. Определить граничные условия для факторов .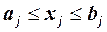

3. Перейти к относительным переменным.

4. Задать порядок аппроксимирующего многочлена (выбрать вид аппроксимирующей зависимости) и установит число искомых коэффициентов l.

5. Разработать план эксперимента.

6. Провести эксперимент и составить таблицу экспериментальных данных.

7. С помощью имеющегося программного обеспечения рассчитать коэффициенты для аппроксимирующей зависимости.

8. Проверить адекватность полученной зависимости.

9. Записать полученную зависимость в форме ограничений для задачи оптимизации.

Познание человеком окружающей его природы началось с эксперимента и до сих пор он остаётся мощным средством решения исследовательских проблем. Это объясняется тем, что некоторые объекты исследования имеют весьма сложную природу и их изучение теоретическими методами не представляется возможным. В полной мере это относится и к исследованиям в области лёгкой промышленности, имеются в виду разработки рациональных конструкций, создание оптимальных технологических процессов, определение способов повышения качества продукции и т.п. Решение подобных задач обычно предполагает постановку многопараметрического (многофакторного) эксперимента, которая может быть выполнена двумя путями.

Классический метод постановки эксперимента заключается в том, что при переходе от опыта к опыту изменяется значение толькоодного входного параметра объекта, в то время как остальные фиксируются на постоянном уровне. Этот метод составляет основу однофакторного эксперимента, при котором находят зависимость исследуемой величины только от одного фактора. При изучении многофакторных систем этот подход часто не оправдывает себя, поскольку даже при ограниченном количестве учитываемых входных параметров требует проведения нереально большого числа опытов. Кроме этого производят большое число однофакторных экспериментов при изучении многофакторной системы, получают частные зависимости, однако объединить их в одну общую невозможно.

Для изучения многофакторных систем наиболее целесообразным является применение статистических методов теории планирования эксперимента. Основы этой теории были впервые опубликованы английским учёным Р. Д. Фишером в 1935 году.

Планирование эксперимента – это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью.

Характерными особенностями процесса планирования эксперимента является стремление минимизировать число опытов; одновременное варьирование всех исследуемых факторов по специальным правилам – алгоритмам; применение математического аппарата, формализующего многие действия исследователя; выбор стратегии, позволяющей принимать обоснованные решения после каждой серии опытов; в ходе эксперимента возможна оптимизация желаемого выходного параметра объекта.

Задачи, для решения которых может использоваться планирование эксперимента, чрезвычайно разнообразны:

- поиск оптимальных условий (оптимизационная – это задача нахождения такого сочетания величин входных параметров объекта, которое обеспечивает оптимальное (максимальное или минимальное) значение выходного параметра);

- построение интерполяционных формул (интерполяционной называется задача нахождения промежуточных значений величины выходного параметра объекта при изменении его входных параметров);

- выбор существенных факторов;

- оценка и уточнение констант теоретических моделей и др.

Дата добавления: 2015-05-26