Норма вектора в евклидовом пространстве. Неравенство Коши-Буняковского

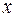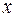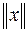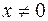Назовем длиной вектора положительное значение . Длину мы будем обозначать через . Так как при и 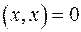только при 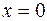, то всякий ненулевой вектор имеет длину, отличную от нуля, и только нулевой вектор имеет длину, равную нулю.

Назовем, далее, вектор 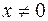нормированным, если его длина равна единице. Легко видеть, что если длина вектора 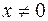не равна единице, то можно этот вектор преобразовать в нормированный вектор. А именно, вектор уже является нормированным, так как

.

Затем назовем векторы 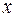и ортогональными (или перпендикулярными), если их скалярное произведение равно нулю.

Очевидно, что нулевой и только нулевой вектор ортогонален самому себе.

Система векторов называется ортогональной, если векторы этой системы попарно ортогональны:

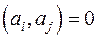при , .

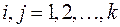Докажем теперь следующее важное свойство ортогональной системы.

Теорема. Всякая ортогональная система ненулевых векторов евклидова пространства 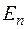линейно независима.

Доказательство. Пусть для этой системы векторов имеет место равенство

,

где − действительные числа. Тогда

.

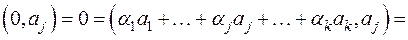
В силу ортогональности 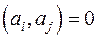при , но 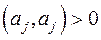, так как 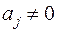. Следовательно, и . Так как − любое из чисел , то , т.е. система векторов линейно независима.

Дата добавления: 2015-05-29