
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение и примеры Евклидовых пространств
|
|
|
|
Евклидово пространство
Т.А. Волкова, Т.П. Кныш.
И КВАДРАТИЧНЫЕ ФОРМЫ
ЕВКЛИДОВО ПРОСТРАНСТВО

Санкт-Петербург
УДК 512.64
ББК 22.143
Рецензент: кандидат технических наук, доцент Шкадова А.Р.
Евклидово пространство и квадратичные формы: конспект лекций. – СПб.: СПГУВК, 2012 – с.
Конспект лекций предназначен для студентов второго курса направления бакалавриата 010400.62 «Прикладная математика и информатика» и первого курса направления бакалавриата 090900.62 «Информационная безопасность».
Пособие содержит полный конспект лекций по одному из разделов дисциплины «Геометрия и алгебра» для направления 010400.62 и дисциплине «Алгебра и геометрия» для направления 090900.62 Учебное пособие соответствует рабочим программам дисциплин, стандартам указанных специальностей и может быть использовано при подготовке к экзамену студентами и преподавателями.
УДК 512.64
ББК 22.143
©Санкт-Петербургский государственный
университет водных коммуникаций, 2012
Многие свойства объектов, встречающихся в геометрии, тесно связаны с возможностью измерения длин отрезков и угла между прямыми. В линейном пространстве мы еще не можем производить такие измерения, вследствие чего область применения общей теории линейных пространств к геометрии и к ряду других математических дисциплин довольно сильно сужается. Это затруднение, однако, может быть устранено, если ввести понятие скалярного произведения двух векторов. А именно, пусть  − линейное
− линейное 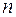 -мерное действительное пространство. Поставим в соответствие каждой паре векторов
-мерное действительное пространство. Поставим в соответствие каждой паре векторов 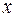 ,
,  действительное число
действительное число  и назовем это число скалярным произведением векторов
и назовем это число скалярным произведением векторов 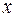 и
и  , если удовлетворяются следующие требования:
, если удовлетворяются следующие требования:
1. 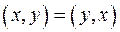 (коммутативный закон).
(коммутативный закон).
2.  ,
,  .
.
3. 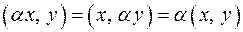 для любого действительного
для любого действительного 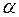 .
.
4.  для любого ненулевого вектора
для любого ненулевого вектора 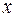 .
.
Скалярное произведение  является частным случаем понятия числовой функции двух векторных аргументов, т. е. функции, значения которой суть числа. Мы можем, следовательно, назвать скалярным произведением такую числовую функцию
является частным случаем понятия числовой функции двух векторных аргументов, т. е. функции, значения которой суть числа. Мы можем, следовательно, назвать скалярным произведением такую числовую функцию  векторных аргументов
векторных аргументов 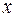 ,
,  , значения которой действительны для любых значений аргументов из
, значения которой действительны для любых значений аргументов из  и для которой удовлетворяются требования 1 − 4.
и для которой удовлетворяются требования 1 − 4.
Действительное линейное пространство  , в котором определено скалярное произведение, будет называться евклидовым и будет обозначаться через
, в котором определено скалярное произведение, будет называться евклидовым и будет обозначаться через 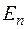 .
.
Отметим, что в евклидовом пространстве 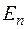 скалярное произведение нулевого вектора на любой вектор равно нулю:
скалярное произведение нулевого вектора на любой вектор равно нулю:  . Действительно,
. Действительно,  , и в силу требования 3
, и в силу требования 3  . Полагая
. Полагая 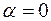 , получаем, что
, получаем, что  . Отсюда, в частности,
. Отсюда, в частности,  .
.
Примеры.
1. Пусть 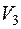 − обычное трехмерное пространство геометрических векторов с общим началом в точке
− обычное трехмерное пространство геометрических векторов с общим началом в точке  . В аналитической геометрии скалярным произведением двух таких векторов называется действительное число, равное
. В аналитической геометрии скалярным произведением двух таких векторов называется действительное число, равное  , где
, где  и
и  − длины векторов
− длины векторов 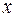 и
и  , а
, а  − угол между векторами
− угол между векторами 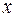 ,
,  , и доказывается, что для этого числа удовлетворяются все требования 1 − 4.
, и доказывается, что для этого числа удовлетворяются все требования 1 − 4.
Таким образом, введенное нами понятие скалярного произведения является обобщением понятия скалярного произведения геометрических векторов.
2. Рассмотрим пространство 
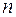 – мерных строк с действительными координатами и поставим в соответствие каждой паре
– мерных строк с действительными координатами и поставим в соответствие каждой паре  и
и  таких векторов-строк действительное число
таких векторов-строк действительное число
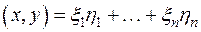
Легко проверить, что для этого числа  удовлетворяются все требования 1 − 4:
удовлетворяются все требования 1 − 4:
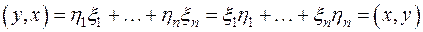
для  и
и 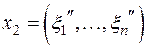 .
.

и аналогично  . Далее,
. Далее,
 ,
,
и аналогично 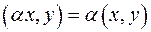 . Наконец,
. Наконец,
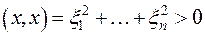 , при
, при 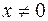 ,
,
так как по меньшей мере одно из чисел 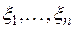 при
при 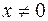 отлично от нуля.
отлично от нуля.
Мы видим отсюда, что это число  является скалярным произведением векторов строк
является скалярным произведением векторов строк 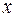 и
и  , а пространство
, а пространство  , после того как мы ввели такое скалярное произведение, становится евклидовым.
, после того как мы ввели такое скалярное произведение, становится евклидовым.
3. Пусть  — линейное действительное
— линейное действительное 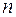 -мерное пространство и
-мерное пространство и 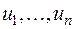 − некоторый его базис. Поставим в соответствие каждой паре векторов
− некоторый его базис. Поставим в соответствие каждой паре векторов 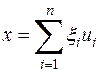 ,
, 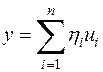 действительное число
действительное число  . Тогда пространство
. Тогда пространство  превратится в евклидово, т. е. число
превратится в евклидово, т. е. число  будет скалярным произведением векторов
будет скалярным произведением векторов 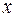 и
и  . В самом деле:
. В самом деле:
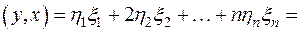
 ,
,
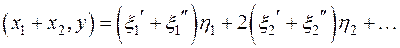
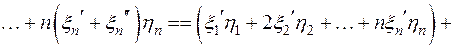

где
 ,
, 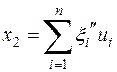 .
.
Затем
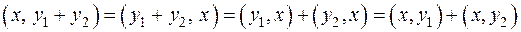
и

 .
.
 .
.
Наконец,
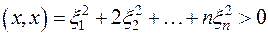 при
при 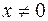
Можно даже другими способами превратить наше пространство  в евклидово, например, мы могли бы поставить в соответствие паре векторов
в евклидово, например, мы могли бы поставить в соответствие паре векторов 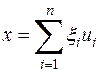 ,
, 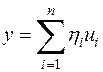 действительное число
действительное число

и легко проверить, что для такого числа  удовлетворяются все требования 1 − 4, характеризующие скалярное произведение. Но так как здесь (при том же базисе
удовлетворяются все требования 1 − 4, характеризующие скалярное произведение. Но так как здесь (при том же базисе 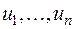 ) мы определили другую числовую функцию
) мы определили другую числовую функцию  , то из
, то из  получается другое евклидово пространство с другим «мероопределением».
получается другое евклидово пространство с другим «мероопределением».
4. Наконец, обращаясь к тому же пространству  , рассмотрим числовую функцию
, рассмотрим числовую функцию  , которая при
, которая при 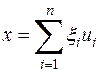 ,
, 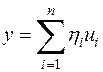 определяется равенством
определяется равенством  . Эта функция уже не является скалярным произведением, так как нарушается требование 4: при
. Эта функция уже не является скалярным произведением, так как нарушается требование 4: при 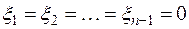 ,
,  вектор
вектор 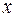 равен
равен  , a
, a 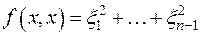 . Тем самым здесь из
. Тем самым здесь из  не получается евклидова пространства.
не получается евклидова пространства.
Пользуясь требованиями 2 и 3, входящими в определение скалярного произведения, легко получить следующую формулу:
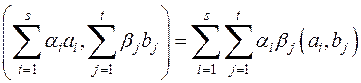 ,
,
где  ,
,  − две произвольные системы векторов. Отсюда, в частности, получается при произвольном базисе
− две произвольные системы векторов. Отсюда, в частности, получается при произвольном базисе 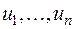 и для любой пары векторов
и для любой пары векторов 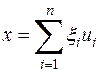 ,
,  , что
, что
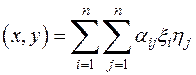 , (1)
, (1)
где  . Выражение в правой части равенства (1) есть многочлен от
. Выражение в правой части равенства (1) есть многочлен от 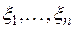 и
и 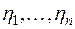 и называется билинейной формой от
и называется билинейной формой от 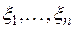 и
и 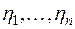 (каждый ее член
(каждый ее член  является линейным, т.е. первой степени, как относительно
является линейным, т.е. первой степени, как относительно  , так и относительно
, так и относительно 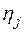 ). Билинейная форма называется симметрической, если для каждого ее коэффициента
). Билинейная форма называется симметрической, если для каждого ее коэффициента  выполняется условие симметрии
выполняется условие симметрии  . Таким образом, скалярное произведение
. Таким образом, скалярное произведение  в произвольном базисе
в произвольном базисе 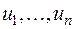 выражается в виде билинейной симметрической формы от координат векторов
выражается в виде билинейной симметрической формы от координат векторов 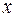 ,
,  с действительными коэффициентами. Но этого еще недостаточно. А именно, полагая
с действительными коэффициентами. Но этого еще недостаточно. А именно, полагая  , получаем из равенства (1), что
, получаем из равенства (1), что
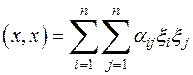 ,
,  (2)
(2)
Выражение в правой части равенства (2) есть многочлен от координат 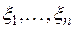 вектора
вектора 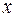 и называется квадратичной формой от
и называется квадратичной формой от 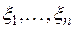 (степень каждого его члена
(степень каждого его члена 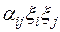 равна двум). Квадратичная форма с действительными коэффициентами называется положительно определенной, если она принимает строго положительное значение при всяком ненулевом наборе действительных значений неизвестных
равна двум). Квадратичная форма с действительными коэффициентами называется положительно определенной, если она принимает строго положительное значение при всяком ненулевом наборе действительных значений неизвестных 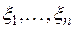 . Таким образом, в силу требования 4 скалярный квадрат
. Таким образом, в силу требования 4 скалярный квадрат  в произвольном базисе
в произвольном базисе 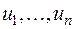 выражается в виде положительно определенной квадратичной формы от
выражается в виде положительно определенной квадратичной формы от 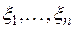 .
.
Можно убедиться, что, обратно, всякая билинейная симметрическая форма с действительными коэффициентами от координат 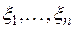 и
и 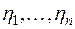 векторов
векторов 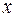 и
и  в некотором базисе
в некотором базисе 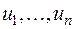 определяет скалярное произведение, если при
определяет скалярное произведение, если при  эта билинейная форма превращается в положительно определенную квадратичную форму.
эта билинейная форма превращается в положительно определенную квадратичную форму.
Итак, в зависимости от выбранного базиса получается для скалярного произведения  та или иная формула. Возникает вопрос: нельзя ли указать такой базис, при котором скалярное произведение имело бы наиболее простое выражение? Чтобы ответить на этот вопрос, введем несколько новых понятий.
та или иная формула. Возникает вопрос: нельзя ли указать такой базис, при котором скалярное произведение имело бы наиболее простое выражение? Чтобы ответить на этот вопрос, введем несколько новых понятий.
|
|
|
|
|
Дата добавления: 2015-05-29; Просмотров: 1612; Нарушение авторских прав?; Мы поможем в написании вашей работы!