Характеристические числа симметрической матрицы

Теорема. Все характеристические числа симметрической матрицы с действительными элементами действительны.

Доказательство. Пусть 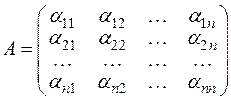− симметрическая матрица 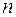-го порядка с действительными элементами, − какое-нибудь ее характеристическое число. Обратимся к линейному комплексному -мерному пространству 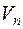и обозначим через 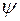линейное преобразование этого пространства, заданное матрицей 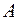в некотором базисе. В пространстве 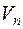, очевидно, 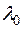будет собственным значением преобразования 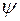, и найдется по меньшей мере один собственный вектор 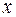, принадлежащий 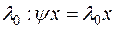. Пусть 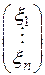− координатный столбец вектора 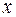, тогда координатный столбец его образа 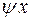будет равен 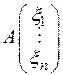, а координатный столбец 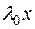будет равен 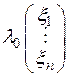, вследствие чего

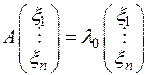. (1)

Транспонируя обе части этого равенства, получаем:

,

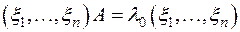так как 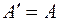. Заменяя в обеих частях последнего равенства числа 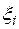, , 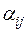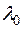сопряженными комплексными числами 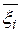, , 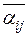, 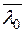находим, что

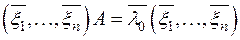, (2)

так как в силу действительности 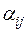сопряженное 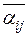равно 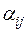. Рассмотрим произведение

.

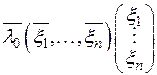Пользуясь равенствами (2) и (1), получаем:

.

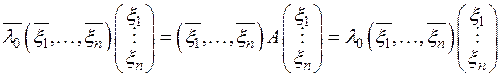Наконец, сокращаем обе части равенства

на 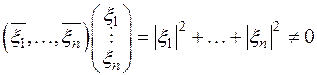(вспомним, 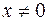). Получаем, что 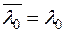, т.е. 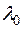действительно, и теорема доказана.

Из этой теоремы вытекает, что все характеристические числа симметрического преобразования 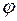евклидова пространства 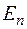являются также и собственными значениями этого преобразования и что для симметрического преобразования 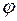существует по меньшей мере один собственный вектор. Но несколько ниже мы покажем, что существует даже ортонормированный базис из собственных векторов. Для этой цели придется доказать несколько лемм.

Лемма. Два собственных вектора, принадлежащих различным собственным значениям симметрического преобразования евклидова пространства 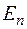, ортогональны.

Доказательство. Пусть 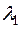и 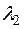− два различных собственных значения симметрического преобразования 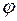, а и 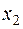− собственные векторы, принадлежащие соответственно 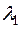и 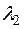. Обратимся к скалярному произведению 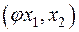. Для него получаем, с одной стороны, что .

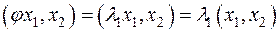С другой стороны, 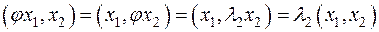. Отсюда 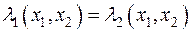. Если бы 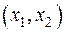не равнялось нулю, то мы в результате сокращения на 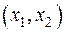получили бы 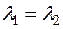, что невозможно. Следовательно, .

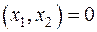Дата добавления: 2015-05-29