
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доказательство
|
|
|
|
1. Пусть для преобразования  существует ортонормированный базис
существует ортонормированный базис  из собственных векторов:
из собственных векторов:  ,
,  (могут встречаться и равные
(могут встречаться и равные 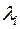 ). В этом базисе преобразование
). В этом базисе преобразование  будет задаваться диагональной матрицей
будет задаваться диагональной матрицей
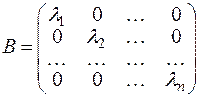 .
.
Но  − симметрическая матрица. Следовательно, по теореме из п. 1.10. преобразование
− симметрическая матрица. Следовательно, по теореме из п. 1.10. преобразование  должно быть симметрическим.
должно быть симметрическим.
2. Обратно, пусть  − симметрическое преобразование пространства
− симметрическое преобразование пространства  . Обозначим через
. Обозначим через  все различные характеристические числа преобразования
все различные характеристические числа преобразования  . В силу теоремы 2 числа
. В силу теоремы 2 числа  и только такие числа являются собственными значениями
и только такие числа являются собственными значениями  . Далее, обозначим через
. Далее, обозначим через  (
( ) подпространство, принадлежащее собственному значению
) подпространство, принадлежащее собственному значению 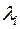 , и через
, и через  − ортонормированный базис
− ортонормированный базис  . По лемме из п. 1.10. каждый вектор подпространства
. По лемме из п. 1.10. каждый вектор подпространства  будет при
будет при  ортогонален к каждому вектору подпространства
ортогонален к каждому вектору подпространства  . Отсюда получается, что система векторов
. Отсюда получается, что система векторов  , получающаяся путем объединения ортонормированных базисов подпространств
, получающаяся путем объединения ортонормированных базисов подпространств  , является ортонормированной. Пусть
, является ортонормированной. Пусть  есть подпространство, натянутое на эту систему векторов. Очевидно, что векторы
есть подпространство, натянутое на эту систему векторов. Очевидно, что векторы 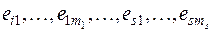 образуют ортонормированный базис подпространства
образуют ортонормированный базис подпространства  и что эти векторы собственные. Если сумма
и что эти векторы собственные. Если сумма 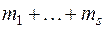 равна
равна  – размерности евклидова пространства
– размерности евклидова пространства  , то
, то  совпадает с
совпадает с  , и теорема будет доказана. Поэтому предположим, что размерность
, и теорема будет доказана. Поэтому предположим, что размерность 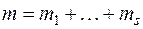 подпространства
подпространства  меньше
меньше  . Тогда по лемме 2 размерность ортогонального дополнения
. Тогда по лемме 2 размерность ортогонального дополнения 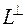 будет равна
будет равна  . Подпространство
. Подпространство  инвариантно относительно
инвариантно относительно  , так как для всякого вектора
, так как для всякого вектора 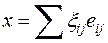 из
из  получаем, что
получаем, что 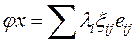 , т.е.
, т.е. 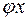 есть также вектор из
есть также вектор из  . Следовательно, по лемме 3 ортогональное дополнение
. Следовательно, по лемме 3 ортогональное дополнение 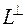 является также инвариантным подпространством относительно
является также инвариантным подпространством относительно  . Симметрическое преобразование
. Симметрическое преобразование  пространства
пространства  , таким образом, индуцирует симметрическое преобразование инвариантного подпространства
, таким образом, индуцирует симметрическое преобразование инвариантного подпространства 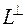 , в силу чего в
, в силу чего в 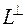 должен существовать по меньшей мере один собственный вектор
должен существовать по меньшей мере один собственный вектор 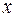 , принадлежащий некоторому собственному значению
, принадлежащий некоторому собственному значению  . Но все собственные векторы уже лежат в
. Но все собственные векторы уже лежат в  . Поэтому вектор
. Поэтому вектор 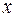 должен одновременно принадлежать
должен одновременно принадлежать  и
и 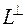 , а это согласно лемме 1 возможно лишь при
, а это согласно лемме 1 возможно лишь при  . Получается противоречие с тем, что
. Получается противоречие с тем, что  (по определению собственный вектор есть, прежде всего, ненулевой вектор). Итак, подпространство
(по определению собственный вектор есть, прежде всего, ненулевой вектор). Итак, подпространство  должно совпадать с
должно совпадать с  , и теорема доказана.
, и теорема доказана.
Обозначим через  матрицу перехода от ортонормированного базиса
матрицу перехода от ортонормированного базиса  к некоторому другому базису
к некоторому другому базису 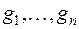 пространства
пространства  . Нетрудно убедиться, что матрица
. Нетрудно убедиться, что матрица  ортогональна тогда и только тогда, когда базис
ортогональна тогда и только тогда, когда базис 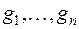 ортонормирован.
ортонормирован.
В самом деле, матрица  задает в ортонормированном базисе
задает в ортонормированном базисе  некоторое линейное преобразование пространства
некоторое линейное преобразование пространства  , переводящее
, переводящее  в базис
в базис 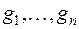 , и это преобразование (а следовательно, и матрица
, и это преобразование (а следовательно, и матрица  ) тогда и только тогда ортогонально, когда базис
) тогда и только тогда ортогонально, когда базис 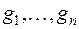 ортонормирован.
ортонормирован.
Пусть теперь симметрическое преобразование  пространства
пространства  задано в некотором ортонормированном базисе симметрической матрицей
задано в некотором ортонормированном базисе симметрической матрицей  . Согласно теореме должен существовать ортонормированный базис из собственных векторов, при котором
. Согласно теореме должен существовать ортонормированный базис из собственных векторов, при котором  задается диагональной матрицей
задается диагональной матрицей  . Матрица
. Матрица  перехода от первоначального базиса к базису из собственных векторов должна быть ортогональной, так как оба базиса ортонормированы. Следовательно, для всякой симметрической матрицы
перехода от первоначального базиса к базису из собственных векторов должна быть ортогональной, так как оба базиса ортонормированы. Следовательно, для всякой симметрической матрицы  с действительными элементами можно подобрать такую ортогональную матрицу
с действительными элементами можно подобрать такую ортогональную матрицу  того же порядка, чтобы
того же порядка, чтобы 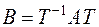 была диагональной матрицей.
была диагональной матрицей.
Покажем, что независимо от выбора ортогональной матрицы  получается единственный диагональный вид
получается единственный диагональный вид 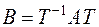 симметрической матрицы
симметрической матрицы  с действительными элементами с точностью до порядка следования диагональных элементов.
с действительными элементами с точностью до порядка следования диагональных элементов.
Пусть эта матрица  приводится к диагональному виду
приводится к диагональному виду
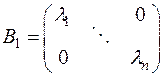
с помощью ортогональной матрицы  и к диагональному виду
и к диагональному виду
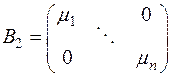
с помошыо ортогональной матрицы  . Так как матрицы
. Так как матрицы  и
и  подобны матрице
подобны матрице  :
:  и
и  , то матрица
, то матрица  подобна матрице
подобна матрице  :
: 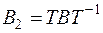 , где
, где  . Отсюда следует, что характеристические многочлены матриц
. Отсюда следует, что характеристические многочлены матриц  и
и  равны:
равны: 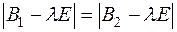 или
или  , откуда диагональные элементы
, откуда диагональные элементы  матрицы
матрицы  с точностью до порядка следования должны совпадать с диагональными элементами
с точностью до порядка следования должны совпадать с диагональными элементами  матрицы
матрицы  (в силу единственности разложения многочлена на неприводимые множители).
(в силу единственности разложения многочлена на неприводимые множители).
Пример. Привести симметрическую матрицу

к диагональному виду с помощью ортогональной матрицы.
Составляем характеристическую матрицу и характеристическое уравнение;

и
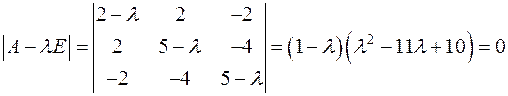 ,
,
откуда получаются характеристические числа 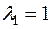 и
и 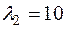 соответственно кратности
соответственно кратности 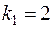 и
и 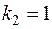 . Находим ортонормированный базис подпространства
. Находим ортонормированный базис подпространства 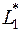 , принадлежащего собственному значению
, принадлежащего собственному значению 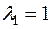 .
.
Ранг матрицы
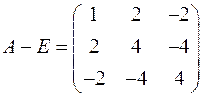
системы линейных однородных уравнении

задающей подпространство 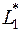 , равен 1. Находим фундаментальную систему решений этой системы линейных однородных уравнений:
, равен 1. Находим фундаментальную систему решений этой системы линейных однородных уравнений: 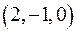 и
и  . Следовательно,
. Следовательно, 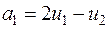 ,
, 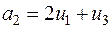 есть базис подпространства
есть базис подпространства 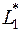 , где
, где 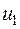 ,
, 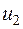 ,
, 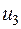 − некоторый ортонормированный базис евклидова пространства
− некоторый ортонормированный базис евклидова пространства  , в котором матрица
, в котором матрица  задает симметрическое преобразование
задает симметрическое преобразование  . Ортогонализируем и нормируем векторы
. Ортогонализируем и нормируем векторы 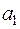 и
и  ; получаем:
; получаем:
 ,
,  .
.
Далее, находим ортонормированный базис подпространства  принадлежащего собственному значению
принадлежащего собственному значению 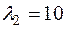 . Ранг матрицы
. Ранг матрицы

системы линейных однородных уравнении

задающей подпространство  , равен 2. Следовательно, фундаментальная система должна состоять из одного решения. Находим его:
, равен 2. Следовательно, фундаментальная система должна состоять из одного решения. Находим его:  . Таким образом, базис подпространства
. Таким образом, базис подпространства  состоит из одного вектора
состоит из одного вектора  . Нормируем
. Нормируем 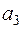 :
:
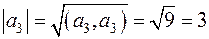 ,
,  .
.
Так как  отлично от
отлично от  , то вектор
, то вектор  должен быть ортогонален к векторам
должен быть ортогонален к векторам  и
и 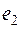 . В качестве контроля можно составить скалярные произведения
. В качестве контроля можно составить скалярные произведения 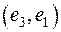 и
и  и убедиться, что они равны нулю.
и убедиться, что они равны нулю.
Итак, нами получена ортонормированная система собственных векторов:
 ,
,  ,
,  .
.
и эта система образует базис всего евклидова пространства  . В базисе
. В базисе  ,
, 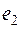 ,
,  симметрическое преобразование
симметрическое преобразование  будет задаваться диагональной матрицей
будет задаваться диагональной матрицей
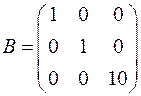 ,
,
и матрицей перехода от первоначального базиса 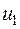 ,
, 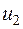 ,
,  к базису
к базису  ,
, 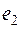 ,
,  будет ортогональная матрица
будет ортогональная матрица
 .
.
Предлагаем в качестве контроля перемножить матрицы  (
(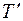 − транспонированная матрица
− транспонированная матрица  ),
),  и
и  и убедиться, что произведение
и убедиться, что произведение 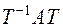 равно диагональной матрице
равно диагональной матрице  .
.
|
|
|
|
|
Дата добавления: 2015-05-29; Просмотров: 724; Нарушение авторских прав?; Мы поможем в написании вашей работы!