Приведение общего уравнения поверхности второго порядка к каноническому виду

В качестве приложения займемся задачей приведения общего уравнения поверхности второго порядка к каноническому виду. Для большего удобства текущие координаты , , 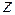обозначим через , , .

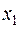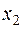. (1)

Сумма первых шести членов левой части уравнения (1) представляет собой действительную квадратичную форму от трех неизвестных , , :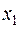

.

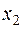По меньшей мере один из коэффициентов формы должен быть отличен от нуля; в противном случае уравнение (1) было бы уравнением плоскости, а не поверхности второго порядка. Приведем форму к каноническому виду с помощью некоторого ортогонального преобразования 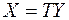. Уравнение (1) поверхности примет вид:

, (2)

причем по меньшей мере одно из характеристических чисел , , должно быть отлично от нуля; если бы это не имело места, то матрица 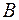канонического вида формы была бы нулевой, а потому матрица первоначальной формы была бы нулевой, т.е. все коэффициенты формы равнялись бы нулю, что невозможно. Мы можем предполагать, что ; в противном случае мы соответствующим образом изменили бы нумерацию неизвестных , , , что равносильно ортогональному преобразованию. Пользуясь тем, что , произведем теперь перенос начала координат в точку , т. е. положим

, , .

Тогда в уравнении (2) исчезнет член , и уравнение примет вид:

, (3)

где . Если и 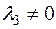, то подобным же образом уничтожатся члены и и уравнение поверхности второго порядка примет вид:

,

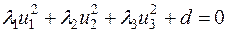т.е. получится каноническое уравнение центральной поверхности.

Уравнение центральной поверхности получается и в том случае, когда , так как тогда уравнение (3) превращается в

.

Поэтому пусть по меньшей мере одно из чисел , не равно нулю. Если, кроме того, , то получается, что

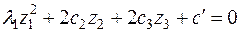. (4)

В этом случае произведем дальнейшее ортогональное преобразование:

, , ,

где 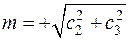, после чего уравнение (4) перейдет в

.

Затем после переноса начала в точку :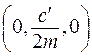

, ,

мы сделаем равным нулю и получим:

,

т.е. получим каноническое уравнение нецентральной поверхности.

Наконец, если только одно из чисел , не равно нулю, например, , а , то уравнение (3) будет выглядеть так:

,

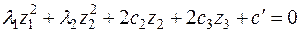и мы можем снова произвести перенос начала:

, , ,

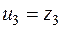после чего получится уравнение

. (5)

В случае мы будем иметь каноническое уравнение

центральной поверхности, а в случае произведем еще раз перенос начала:

, , ,

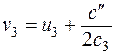после которого уравнение (5) перейдет в каноническое уравнение нецентральной поверхности:

, .

Итак, с помощью ортогональных преобразований и переносов начала уравнение (1) поверхности второго порядка преобразуется либо в каноническое уравнение центральной поверхности:

, ,

либо в каноническое уравнение нецентральной поверхности:

, .

Отметим в заключение, что поверхность второго порядка называется вырожденной цилиндрической, если в ее каноническом уравнении отсутствует хотя бы одна текущая координата.

Литература

1. Ван дер Варден Б.Л. Алгебра. - СПб.: Лань, 2004. - 624 с.

2. Кныш Т.П. Линейные пространства. Конспект лекций. - СПГУВК. СПб., 2010.-69 с.

3. Привалов И.И. Аналитическая геометрия. - СПб.; М.; Краснодар: Лань, 2007. - 304 с.

4. Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии. - СПб.: Лань, 2007. - 336 с.

5. Фаддеев Д.К., Соминский И.С. Задачи по высшей алгебре. - СПб.; М.; Краснодар: Лань, 2007. - 288 с.

6. Курош А.Г. Курс высшей алгебры. - СПб.; М.; Краснодар: Лань, физматкнига, 2007. - 432 с.

7. Окунев Л.Я. Высшая алгебра.- СПб.: Лань, 2009. - 336 с.

Содержание

Евклидово пространство. 4

1.1. Определение и примеры Евклидовых пространств. 4

1.2. Норма вектора в Евклидовом пространстве. Неравенство Коши-Буняковского 10

1.3. Ортонормирование векторов в Евклидовом пространстве. 11

1.4. Процесс ортогонализации Грамма-Шмидта. 12

1.5. Ортонормированный базис и скалярное произведение в нём. 15

1.6. Изоморфизм евклидовых пространств. 16

1.7. Ортогональное преобразование. 18

1.8. Матрица ортогонального преобразования. 20

1.9. Симметрическое преобразование. 24

1.10. Характеристические числа симметрической матрицы.. 27

1.11. Ортогональное дополнение пространства. 29

2. Квадратичные формы.. 37

2.1. Квадратичные формы и приведение их к каноническому виду. 37

2.2. Ранг квадратичной формы.. 41

2.3. Закон инерции. 48

2.4. Приведение квадратичной формы к главным осям. 53

2.5. Приведение общего уравнения поверхности второго порядка к каноническому виду. 58

Литература. 62

Содержание. 63

Волкова Тамара Александровна, Кныш Татьяна Петровна

Евклидово пространство и квадратичные формы

Конспект лекций

[1] Здесь и далее, числа будут чаще обозначаться не греческими, а малыми латинскими буквами.

Дата добавления: 2015-05-29