
- Р Р‡.МессенРТвЂВВВВВВВВжер
- ВКонтакте
- РћРТвЂВВВВВВВВнокласснРСвЂВВВВВВВВРєРСвЂВВВВВВВВ
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВВВВВВВРЎР‚
- LiveJournal
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приведение квадратичной формы к главным осям
|
|
|
|
На протяжении предыдущих параграфов мы говорили о приведении квадратичной формы над числовым полем к каноническому виду с помощью линейного невырожденного преобразования неизвестных.
Никаких особых ограничений на линейные невырожденные преобразования не накладывались: они могли быть любыми с коэффициентами из данного числового поля, лишь бы квадратичные формы приводились к каноническому виду. В аналитической геометрии приведение кривых и поверхностей второго порядка к каноническому виду достигается, однако, не произвольным образом, а с помощью специального класса линейных преобразований.
Эти преобразования, известные под названием ортогональных, можно перенести и на общий случай действительных квадратичных форм 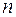 неизвестных и развить теорию приведения квадратичных форм к главным осям, теорию, имеющую глубокие приложения в различных приложениях математики, в механике и в физике.
неизвестных и развить теорию приведения квадратичных форм к главным осям, теорию, имеющую глубокие приложения в различных приложениях математики, в механике и в физике.
Докажем прежде всего следующую основную теорему.
Теорема (о приведении квадратичной формы к главным осям). Всякую квадратичную форму 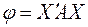 с действительными коэффициентами от
с действительными коэффициентами от 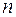 неизвестных
неизвестных 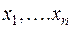 можно привести к каноническому виду с помощью ортогонального преобразования неизвестных.
можно привести к каноническому виду с помощью ортогонального преобразования неизвестных.
Доказательство. Так как матрица  квадратичной формы
квадратичной формы  есть симметрическая матрица
есть симметрическая матрица 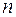 -го порядка с действительными элементами, то ее можно привести к диагональному виду
-го порядка с действительными элементами, то ее можно привести к диагональному виду
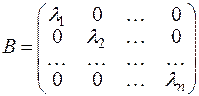
с помощью ортогональной матрицы 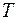 того же порядка:
того же порядка: 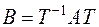 . Но ортогональная матрица обладает тем свойством, что ее обратная матрица равна транспонированной матрице; следовательно,
. Но ортогональная матрица обладает тем свойством, что ее обратная матрица равна транспонированной матрице; следовательно, 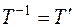 , и мы можем написать, что
, и мы можем написать, что 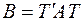 .
.
Подвергнем теперь неизвестные ортогональному линейному преобразованию 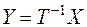 или
или 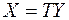 . Тогда квадратичная форма
. Тогда квадратичная форма  перейдет в квадратичную форму с матрицей
перейдет в квадратичную форму с матрицей 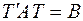 , т.е. приведется к каноническому виду
, т.е. приведется к каноническому виду
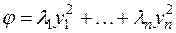 .
.
Пример. Привести к главным осям квадратичную форму
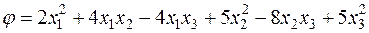 ,
,
т.е. привести эту форму к каноническому виду с помощью ортогонального преобразования неизвестных.
Решение. Составляем матрицу  квадратичной формы
квадратичной формы  :
:
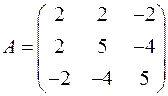
и приводим матрицу  к диагональному виду с помощью некоторой ортогональной матрицы. Но в примере, рассмотренном ранее, мы уже нашли диагональный вид
к диагональному виду с помощью некоторой ортогональной матрицы. Но в примере, рассмотренном ранее, мы уже нашли диагональный вид 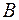 этой матрицы
этой матрицы  и ортогональную матрицу
и ортогональную матрицу 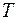 :
:
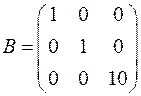 ,
,
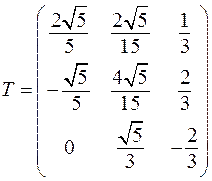 .
.
Таким образом, данная квадратичная форма приводится к каноническому виду
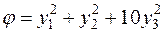
с помощью ортогонального преобразования 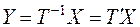 , или подробнее:
, или подробнее:
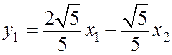 ,
,
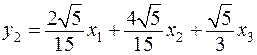 ,
,
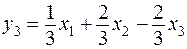 .
.
Впрочем, ортогональное преобразование можно записать в виде 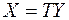 , что часто оказывается более удобным. Имеем:
, что часто оказывается более удобным. Имеем:
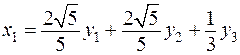 ,
,
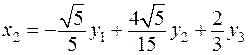 ,
,
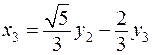 .
.
Действительная квадратичная форма, т.е. форма с действительными коэффициентами, может быть приведена к каноническому виду различными ортогональными преобразованиями. Но мы сейчас увидим, что все эти ортогональные преобразования приводят данную квадратичную форму к одному и тому же каноническому виду с точностью до порядка следования членов.
Теорема (о единственности канонического вида). При любом ортогональном преобразовании неизвестных 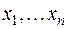 , приводящем действительную квадратичную форму
, приводящем действительную квадратичную форму 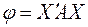 к каноническому виду, получается с точностью до порядка следования членов один и тот же канонический вид:
к каноническому виду, получается с точностью до порядка следования членов один и тот же канонический вид:
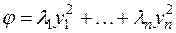 , (1)
, (1)
причем коэффициентами этого канонического вида являются характеристические числа матрицы  квадратичной формы
квадратичной формы  , и каждый из этих чисел встречается в каноническом виде (1) в качестве коэффициента столько раз, какова кратность этого числа.
, и каждый из этих чисел встречается в каноническом виде (1) в качестве коэффициента столько раз, какова кратность этого числа.
Доказательство. Пусть данная квадратичная форма  с помощью ортогонального преобразования
с помощью ортогонального преобразования 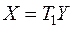 приводится к каноническому виду (1) и с помощью преобразования
приводится к каноническому виду (1) и с помощью преобразования 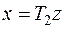 приводится к каноническому виду
приводится к каноническому виду
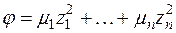 . (2)
. (2)
Обозначим через 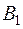 и
и 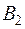 соответственно матрицу канонического вида (1) и матрицу канонического вида (2). Это будут, очевидно, диагональные матрицы, причем
соответственно матрицу канонического вида (1) и матрицу канонического вида (2). Это будут, очевидно, диагональные матрицы, причем 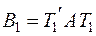 и
и 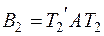 . Так как
. Так как  и
и 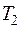 − ортогональные матрицы, то
− ортогональные матрицы, то 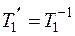 и
и  , в силу чего
, в силу чего
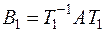 ,
, 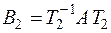 .
.
Но в [2] было показано, что независимо от выбора ортогональной матрицы 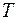 получается единственный диагональный вид
получается единственный диагональный вид 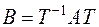 симметрической матрицы
симметрической матрицы  с действительными элементами с точностью до порядка следования диагональных элементов. Поэтому канонический вид (2) должен с точностью до порядка следования членов совпадать с каноническим видом (1), т.е. при соответствующей нумерации неизвестных
с действительными элементами с точностью до порядка следования диагональных элементов. Поэтому канонический вид (2) должен с точностью до порядка следования членов совпадать с каноническим видом (1), т.е. при соответствующей нумерации неизвестных 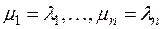 .
.
Далее, в силу подобия матрицы  и
и 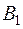 должны иметь одни и те же характеристические числа. Но
должны иметь одни и те же характеристические числа. Но
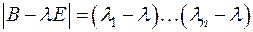 ,
,
откуда 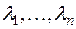 − характеристические числа матрицы
− характеристические числа матрицы 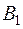 и, следовательно, матрицы
и, следовательно, матрицы  . Пусть при соответствующей нумерации
. Пусть при соответствующей нумерации 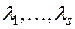 (
(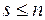 ) все различные характеристические числа матрицы
) все различные характеристические числа матрицы  с кратностями, равными соответственно
с кратностями, равными соответственно 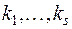 (
(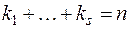 ). Тогда
). Тогда 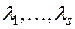 будут встречаться в диагональном виде
будут встречаться в диагональном виде 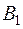 соответственно
соответственно 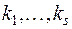 раз, т.е. каждый из характеристических чисел
раз, т.е. каждый из характеристических чисел 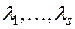 будет встречаться в каноническом виде (1) в качестве коэффициента столько раз, какова его кратность.
будет встречаться в каноническом виде (1) в качестве коэффициента столько раз, какова его кратность.
|
|
|
Дата добавления: 2015-05-29; Просмотров: 5662; Нарушение авторских прав?; Мы поможем в написании вашей работы!