Квадратичные формы и приведение их к каноническому виду

Квадратичные формы

Теория квадратичных форм тесно связана с задачей приведения уравнений кривых и поверхностей второго порядка к каноническому виду. Поэтому вполне естественно начать с рассмотрения некоторых соотношений из аналитической геометрии.

Как известно, общее уравнение кривой второго порядка имеет следующий вид:

. (1)

Если (1) есть уравнение центральной кривой второго порядка, то путем переноса начала координат в центр можно уничтожить члены первой степени, и уравнение кривой примет более простой вид:

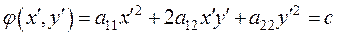, (2)

где 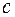− некоторое число[1]. Мы получили в левой части уравнения квадратичную форму от неизвестных , :

.

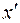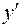С помощью поворота прямоугольной системы на соответствующий угол уравнение (2) можно привести к каноническому виду:

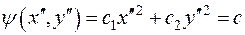
Иными словами, в левой части уравнения получится так называемая каноническая квадратичная форма:

, (*)

содержащая только члены с квадратами неизвестных.

Дадим теперь задаче приведения уравнения кривой 2-го порядка к каноническому виду алгебраическое истолкование.

Приведение уравнения (2) к каноническому виду достигается с помощью поворота прямоугольной системы координат. Запишем это преобразование алгебраически:

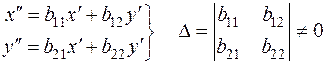, (3)

т.е. мы имеем просто невырожденное линейное преобразование двух неизвестных.

Итак, мы приходим к следующей алгебраической задаче: с помощью линейного невырожденного преобразования (3) привести квадратичную форму 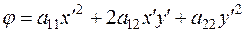к каноническому виду (*).

Эту задачу можно обобщить на случай любого числа неизвестных. Рассмотрим квадратичную форму от 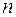неизвестных:

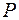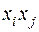над числовым полем . Коэффициенты при мы будем всегда обозначать через а коэффициенты при − через 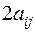(). Полагая , мы можем квадратичную форму (4) записать сокращенно в виде суммы .

Квадратичную форму вида 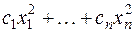мы будем называть канонической (некоторые коэффициенты 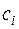могут равняться нулю).

Оказывается, квадратичную форму (4) всегда можно привести к каноническому виду с помощью некоторого линейного невырожденного преобразования неизвестных () с коэффициентами из того же поля .

Это приведение к каноническому виду достигается различными способами. Мы изложим идею одного из наиболее простых методов, а именно метод Лагранжа. Для большей наглядности обратимся к конкретному примеру.

Пример. Привести к каноническому виду квадратичную форму 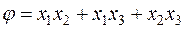с помощью линейного невырожденного преобразования неизвестных.

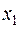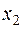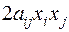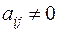Здесь отсутствуют члены с квадратами неизвестных, т.е. все коэффициенты равны нулю. Подвергнем неизвестные , , такому линейному невырожденному преобразованию, чтобы в квадратичной форме появился хотя бы один член с квадратом неизвестного. Обратимся к члену с , например к 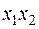. Применим к неизвестным линейное преобразование:

(5)

Это преобразование невырожденное, так как

Получаем: .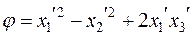

Если вместо 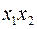обратиться к другому члену 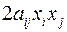с , например , то для получения члена с квадратом неизвестного придется ввести несколько иное невырожденное преобразование

, , .

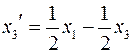Теперь группируем члены 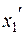(или с 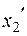) и дополняем их до полного квадрата:

.

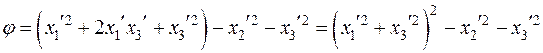Затем подвергаем неизвестные дальнейшему линейному невырожденному преобразованию:

, , . (6)

Получаем канонический вид:

.

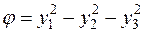Остается найти линейное невырожденное преобразование, заменяющее линейные преобразования (5) и (6). Выпишем их матрицы:

, .

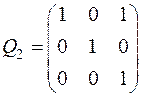Произведение 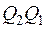этих матриц и будет матрицей искомого преобразования. Пользуясь правилом перемножения матриц, нетрудно найти, что

,

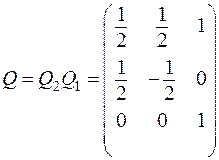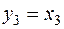, , (7)

и будет искомым преобразованием, приводящим заданную квадратичную форму к каноническому виду.

Впрочем, преобразование (7) можно получить и другим способом: подставим в (6) значения из (5). Получим как раз искомое преобразование (7).

Дата добавления: 2015-05-29