Закон инерции

Квадратичная форма может быть приведена к каноническому виду весьма разнообразными способами. Однако если форма действительна, т.е. имеет действительные коэффициенты, то оказывается справедливой следующая теорема.

Закон инерции квадратичных форм. Если действительная квадратичная форм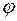а ранга 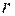приведена двумя действительными (т.е. с действительными коэффициентами) линейными невырожденными преобразованиями соответственно к виду

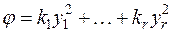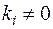(), (1)

и к виду

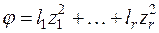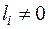(), (2)

то формы (1) и (2) имеют одно и то же число положительных членов.

Доказательство. Без ограничения общности доказательства можно предположить, что в формах (1) и (2) сначала идут положительные члены, так как иначе мы изменили бы соответствующим образом нумерацию неизвестных. Итак, пусть

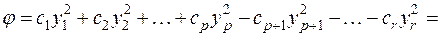
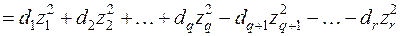(3)

.

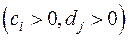Нам надо доказать, что .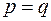

Предположим противное, пусть, например, 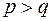. Неизвестные 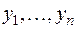и 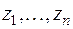линейно выражаются через старые неизвестные 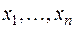. Поэтому есл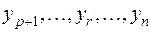и и 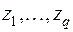приравнять равными нулю, то получится система 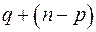линейных однородных уравнений:

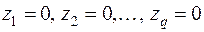
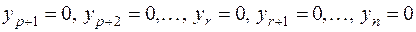
с действительными коэффициентами относительно 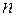неизвестных .

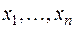Очевидно, эта система допускает в поле действительных чисел ненулевые решения, так как число уравнений меньше числа неизвестных: .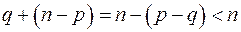

Пусть 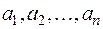− одно из ненулевых решений системы в поле действительных чисел. Заменим в равенстве (3) неизвестные 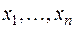действительными числами 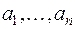; тогда получим

.

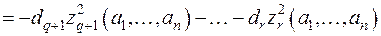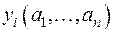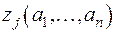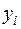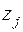Через и здесь обозначены значения неизвестных и при .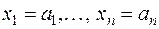

Выражение в левой части не может быть отрицательным, а в правой части выражение не может быть положительным. Следовательно, обе части рассматриваемого равенства должны обращаться в нуль, а это возможно только в том случае, когда

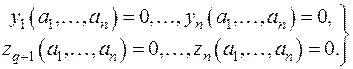(4)

Но выше мы подобрали 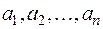так, чтобы

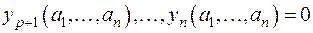. (5)

Таким образом, сопоставляя равенства (4) и (5), мы приходим к выводу, что 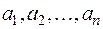есть ненулевое решение системы

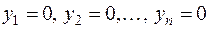
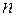линейных однородных уравнений с 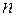неизвестными. Но в таком случае определитель этой системы должен равняться нулю, т.е. преобразование, переводящее старые неизвестные 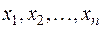в новые 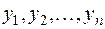, является вырожденным. Получилось противоречие, которое и доказывает теорему.

Мы будем называть указателем действительной квадратичной формы число положительных членов в ее канонической записи.

Итак, всякая действительная квадратичная форма характеризуется двумя числами − рангом и указателем. Эти числа не зависят от действительного невырожденного преобразования: они инвариантны относительно таких преобразований.

Закон инерции играет большую роль при классификации действительных квадратичных форм. Назовем две действительные формы 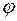и 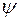эквивалентными по отношению к невырожденному действительному преобразованию 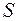, если 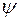получается из 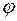с помощью преобразования 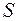. Очевидно, что в силу теоремы предыдущего параграфа и закона инерции две действительные эквивалентные квадратичные формы 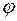и 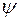должны обладать одним и тем же рангом и указателем.

Но справедливо и обратное утверждение: если две действительные квадратичные формы 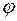и 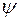имеют одинаковый ранг и указатель, то они эквиваленты по отношению к действительному невырожденному преобразованию.

Для доказательства этого утверждения введем следующее определение.

Определение. Действительная квадратичная каноническая форма

,

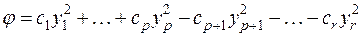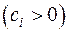
называется нормальной, если все коэффициенты 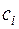равны единице, т. е.

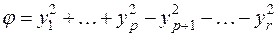
(при 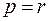члены с 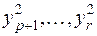отпадают). Очевидно, что всякую действительную квадратичную форму можно невырожденным действительным преобразованием переменных привести к нормальному виду. В самом деле, можно сначала методом Лагранжа квадратичную форму привести к каноническому виду:

, ,

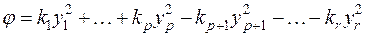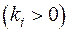а затем подвергнуть неизвестные 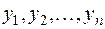невырожденному действительному преобразованию

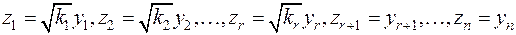
(при 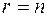последние 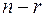равенств отпадают), в результате чего получится форма нормального вида:

.

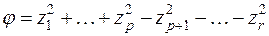Теперь вернемся к доказательству нашего утверждения.

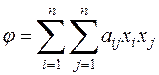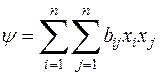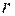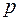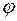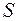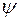Доказательство. Итак, пусть две действительные формы и имеют один и тот же ранг и указатель . Пусть приводится к нормальному виду действительным невырожденным преобразованием , а − действительным невырожденным преобразованием 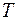. Согласно теореме предыдущего параграфа и закону инерции как 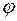, так и 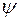приводятся к одному и тому же нормальному виду:

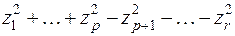, (4)

потому что ранг и указатель у форм 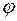и 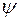одинаковы.

Таким образом, если форму 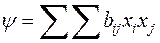подвергнуть преобразованию 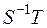, то получится форма 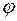. Действительно, с помощью преобразования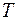 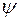переходит в нормальный вид (А), а затем с помощью преобразования 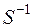− в .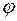

Так как, очевидно, 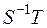является действительным невырожденным преобразованием, то наше утверждение полностью доказано.

Для наглядности приведем пример, иллюстрирующий доказательство.

Пример. Рассмотрим две квадратичные формы:

,

.

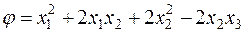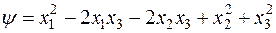Они имеют одинаковый ранг и указатель, а именно: 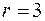, 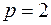. Легко проверить, что невырожденные преобразования:

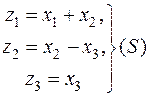
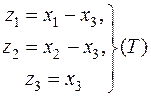
приводят соответственно формы и к нормальному виду:

.

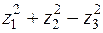Следовательно, преобразование 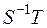должно переводить 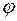в 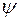. Найдем 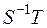, для этого выписываем матрицы преобразовани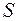й и :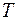

, .

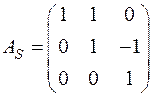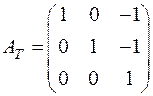Откуда

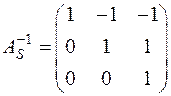и .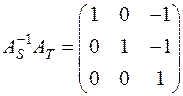

Таким образом, преобразование 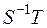найдено; оно имеет вид:

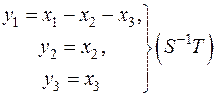
и превращает форму 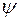в

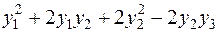(6)

Но форма (6) тождественна с 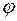, так как отличается от нее только обозначением переменных.

Для квадратичных форм над полем комплексных чисел закон инерции и все его следствия теряют смысл. Однако квадратичную форму над полем комплексных чисел всегда можно привести к сумме квадратов

,

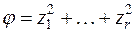
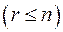с помощью линейного невырожденного преобразования неизвестных с комплексными коэффициентами. В самом деле, для этого форму следует сначала привести к каноническому виду

,

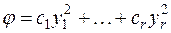
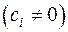а затем подвергнуть 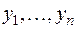невырожденному преобразованию

,

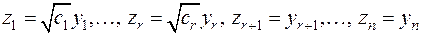в результате чего получится сумма квадратов (в случае 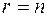последние 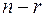равенств отпадают):

.

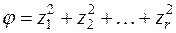Дата добавления: 2015-05-29