
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ранг квадратичной формы
|
|
|
|
Итак, всякую квадратичную форму можно методом Лагранжа можно привести к виду:
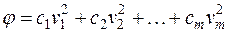 , (1)
, (1)
где 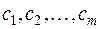 отличны от нуля.
отличны от нуля.
Возникает естественный вопрос: чему равно число 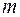 квадратов, входящих в каноническую форму (1)? Ниже мы увидим, что на этот вопрос можно дать вполне определенный ответ.
квадратов, входящих в каноническую форму (1)? Ниже мы увидим, что на этот вопрос можно дать вполне определенный ответ.
Составим квадратную матрицу 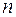 -го порядка
-го порядка
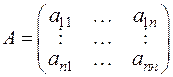
из коэффициентов 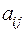 квадратичной формы
квадратичной формы 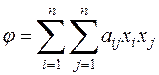 . Будем называть
. Будем называть  матрицей формы
матрицей формы  , а ранг
, а ранг  − рангом формы
− рангом формы  .
.
Так как в квадратичной форме 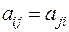 , то матрица
, то матрица  не меняется при транспонировании. Матрица
не меняется при транспонировании. Матрица 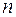 -го порядка, остающаяся без изменения при транспонировании, называется, как известно, симметрической.
-го порядка, остающаяся без изменения при транспонировании, называется, как известно, симметрической.
Покажем, что своей матрицей  квадратичная форма определяется вполне однозначно.
квадратичная форма определяется вполне однозначно.
Пусть  и
и 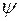 − две квадратичные формы от
− две квадратичные формы от 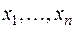 , у которых матрицы
, у которых матрицы 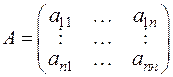 и
и 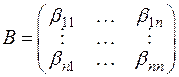 равны. Тогда
равны. Тогда 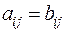 (
(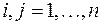 ) и члены
) и члены 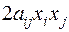 и
и 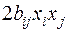 (
(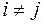 ), а также
), а также 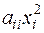 и
и 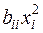 равны, откуда согласно определению равенства многочленов от нескольких неизвестных следует, что
равны, откуда согласно определению равенства многочленов от нескольких неизвестных следует, что 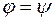 .
.
Обратно, пусть квадратичные формы 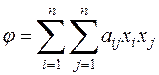 и
и 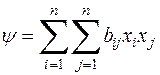 равны. Пользуясь снова понятием равенства многочленов от нескольких неизвестных, находим, что члены
равны. Пользуясь снова понятием равенства многочленов от нескольких неизвестных, находим, что члены 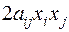 и
и 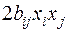 (
(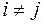 ),
), 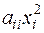 и
и 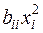 должны быть равны, откуда
должны быть равны, откуда 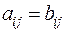 (
(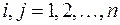 ) и
) и 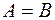 .
.
Нашей основной задачей, является доказательство следующей теоремы.
Теорема. От невырожденного линейного преобразования ранг формы  не изменяется.
не изменяется.
Прежде чем переходить к доказательству этой теоремы, введем матричный вид записи квадратичной формы и займемся некоторыми свойствами матриц 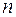 -го порядка, связанными с рангом матрицы.
-го порядка, связанными с рангом матрицы.
Обозначим через 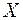 матрицу-столбец:
матрицу-столбец:
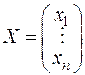 ,
,
составленную из неизвестных 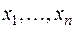 . Тогда квадратичная форма
. Тогда квадратичная форма 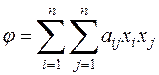 (
(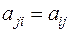 ) запишется в виде
) запишется в виде
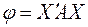 ,
,
где 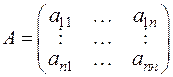 − матрица квадратичной формы, а
− матрица квадратичной формы, а 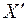 − транспонированная матрица
− транспонированная матрица 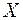 , т.е.
, т.е.  .
.
В самом деле, по правилу перемножения матриц получаем, что
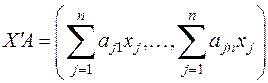 ,
,
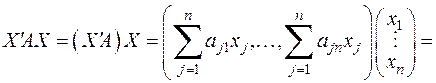
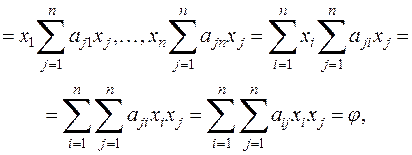
так как 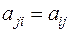 .
.
Пусть 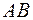 есть произведение матриц:
есть произведение матриц:
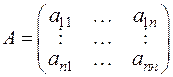 и
и 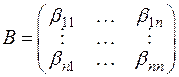 .
.
Что можно сказать относительно ранга 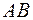 ? Мы сейчас покажем, что ранг произведения двух матриц не выше ранга каждого из сомножителей.
? Мы сейчас покажем, что ранг произведения двух матриц не выше ранга каждого из сомножителей.
В самом деле, если  − элемент матрицы
− элемент матрицы 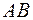 , то по правилу перемножения
, то по правилу перемножения
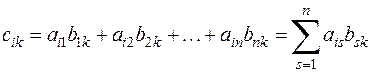 (
(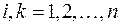 ).
).
Таким образом, каждый элемент 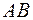 есть сумма
есть сумма 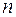 слагаемых. Обозначим теперь ранг матрицы
слагаемых. Обозначим теперь ранг матрицы  через
через 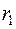 , а ранг матрицы
, а ранг матрицы 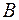 через
через 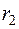 и покажем, что любой минор
и покажем, что любой минор 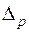 (
(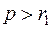 )
) 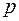 -го порядка матрицы
-го порядка матрицы 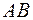 равен нулю. Определитель
равен нулю. Определитель 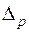 можно, очевидно, разложить на сумму определителей типа
можно, очевидно, разложить на сумму определителей типа
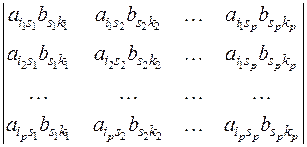 , (2)
, (2)
так как элемент каждого столбца 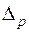 есть сумма
есть сумма 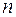 слагаемых. Вынося из каждого столбца определителя (2) общий множитель, получим:
слагаемых. Вынося из каждого столбца определителя (2) общий множитель, получим:
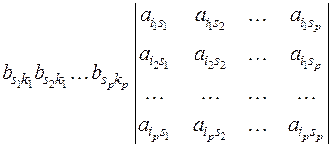 .
.
Последний определитель может иметь некоторые строки или столбцы одинаковыми, но может также иметь и различные строки и столбцы. В первом случае он, очевидно, равен нулю. Но и во втором случае определитель равен нулю, так как он будет минором 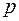 -го порядка (
-го порядка (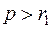 ) матрицы
) матрицы  ранга
ранга 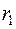 .
.
Итак, мы видим, что 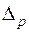 равно нулю, так как все его слагаемые (2) равны нулю. Этим вполне доказано, что ранг
равно нулю, так как все его слагаемые (2) равны нулю. Этим вполне доказано, что ранг 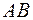 не может быть выше ранга
не может быть выше ранга  .
.
Остается показать, что ранг 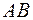 не выше ранга второго сомножителя
не выше ранга второго сомножителя 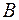 . Обращаемся к транспонированной матрице
. Обращаемся к транспонированной матрице 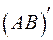 . Ее ранг, с одной стороны, равен рангу
. Ее ранг, с одной стороны, равен рангу 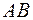 . С другой стороны,
. С другой стороны, 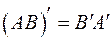 , а отсюда, пользуясь результатом, полученным для первого сомножителя, находим, что ранг
, а отсюда, пользуясь результатом, полученным для первого сомножителя, находим, что ранг 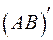 не может быть выше ранга
не может быть выше ранга 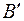 . Но ранг транспонированной матрицы
. Но ранг транспонированной матрицы 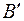 равен рангу
равен рангу 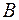 . Таким образом, ранг
. Таким образом, ранг 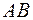 не может быть выше ранга
не может быть выше ранга 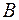 .
.
Особенно важен для нас тот частный случай, когда один из сомножителей, например 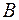 , есть невырожденная матрица.
, есть невырожденная матрица.
Если матрица  ранга
ранга 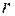 умножается (слева или справа) на невырожденную матрицу
умножается (слева или справа) на невырожденную матрицу 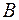 , то ранг произведения также равен
, то ранг произведения также равен 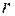 .
.
Доказывается это довольно просто. С одной стороны, ранг 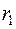 произведения
произведения 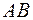 , как мы уже знаем, меньше или равен рангу матрицы
, как мы уже знаем, меньше или равен рангу матрицы  :
: 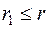 . С другой стороны, умножив
. С другой стороны, умножив 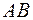 справа на
справа на 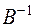 , получим:
, получим: 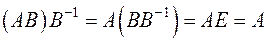 .
.
Здесь  является произведением
является произведением 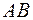 на
на 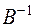 ; поэтому ранг
; поэтому ранг  меньше или равен рангу матрицы
меньше или равен рангу матрицы 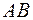 :
:  . Но неравенства
. Но неравенства 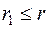 ,
,  как раз свидетельствуют о том, что
как раз свидетельствуют о том, что 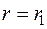 .
.
Для произведения 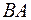 доказательство приводится аналогично.
доказательство приводится аналогично.
Теперь мы в состоянии доказать нашу теорему.
Доказательство. Квадратичную форму
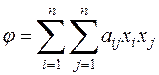
удобнее записать в матричном виде
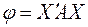 , (3)
, (3)
где 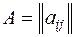 ,
, 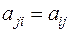 − матрица
− матрица  ,
, 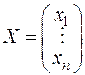 и
и 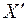 − транспонированная матрица
− транспонированная матрица 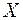 .
.
Подвергнем  невырожденному линейному преобразованию:
невырожденному линейному преобразованию:
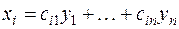 (
( ). (4)
). (4)
Здесь в отличие от предыдущего старые неизвестные выражаются через новые. Обозначим через 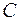 матрицу этого преобразования:
матрицу этого преобразования: 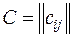 . Линейное преобразование (4) можно записать в матричном виде:
. Линейное преобразование (4) можно записать в матричном виде:
 , где
, где 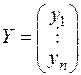 .
.
Подставляя это выражение 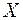 в правую часть равенства (3), получаем:
в правую часть равенства (3), получаем: 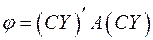 , или, так как
, или, так как 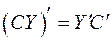 :
:
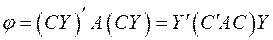 .
.
Матрица 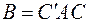 является также симметрической, так как
является также симметрической, так как 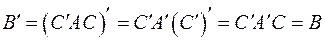 (очевидно,
(очевидно, 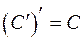 , а
, а 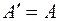 благодаря тому, что
благодаря тому, что  − симметрическая матрица). Мы видим отсюда, что
− симметрическая матрица). Мы видим отсюда, что 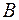 − матрица преобразованной квадратичной формы.
− матрица преобразованной квадратичной формы.
Итак, при линейном преобразовании (4) неизвестных 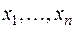 с матрицей
с матрицей 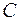 (старые неизвестные выражаются через новые) матрица В преобразованной квадратичной формы выражается через матрицу
(старые неизвестные выражаются через новые) матрица В преобразованной квадратичной формы выражается через матрицу  первоначальной квадратичной формы следующим образом:
первоначальной квадратичной формы следующим образом: 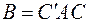 .
.
Отсюда, так как 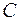 − невырожденная матрица, ранг
− невырожденная матрица, ранг 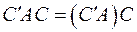 равен рангу
равен рангу 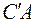 ; в свою очередь ранг
; в свою очередь ранг 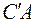 равен рангу
равен рангу  , поскольку
, поскольку 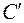 также невырожденная матрица. Следовательно, ранг преобразованной квадратичной формы равен рангу первоначальной формы. Теорема доказана.
также невырожденная матрица. Следовательно, ранг преобразованной квадратичной формы равен рангу первоначальной формы. Теорема доказана.
Выражение 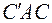 нельзя смешивать с выражением
нельзя смешивать с выражением 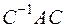 , так как, вообще говоря, матрица
, так как, вообще говоря, матрица 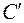 не равна обратной матрице
не равна обратной матрице 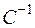 .
.
Вернемся к вопросу, заданному в самом начале параграфа. Чему равно число членов 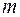 канонического вида (1)? Оказывается, что
канонического вида (1)? Оказывается, что 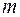 равно рангу формы
равно рангу формы  .
.
Следствие. Если  − квадратичная форма ранга
− квадратичная форма ранга 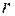 , то после приведения ее линейным невырожденным преобразованием к каноническому виду она будет содержать
, то после приведения ее линейным невырожденным преобразованием к каноническому виду она будет содержать 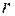 отличных от нуля членов.
отличных от нуля членов.
В самом деле, пусть квадратичная форма  ранга
ранга 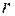 приведена к каноническому виду (1). Матрица формы (1), очевидно, равна:
приведена к каноническому виду (1). Матрица формы (1), очевидно, равна:
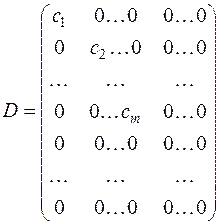
(Если 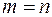 , то последние
, то последние 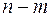 строк и
строк и 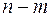 столбцов отпадают.), откуда ясно, что ранг
столбцов отпадают.), откуда ясно, что ранг 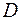 равен
равен 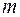 . Но, с другой стороны, ранг формы
. Но, с другой стороны, ранг формы  от невырожденного преобразования не меняется; следовательно,
от невырожденного преобразования не меняется; следовательно, 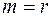 , что и требовалось показать.
, что и требовалось показать.
В заключение разберем пример, иллюстрирующий вышеизложенное.
Пример. Рассмотрим форму 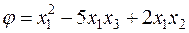 . Ее ранг равен двум, так как ранг ее матрицы
. Ее ранг равен двум, так как ранг ее матрицы
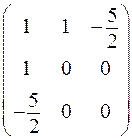
равен 2. Следовательно, после приведения к каноническому виду с помощью линейного невырожденного преобразования должно получиться два отличных от нуля члена независимо от способа приведения. И действительно, преобразуя  методом Лагранжа, получим канонический вид
методом Лагранжа, получим канонический вид 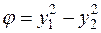 , причем
, причем 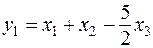 ,
, 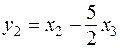 ,
, 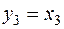 .
.
|
|
|
|
|
Дата добавления: 2015-05-29; Просмотров: 1694; Нарушение авторских прав?; Мы поможем в написании вашей работы!